👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
参考文献:

本文采用的是换一个算法解决, 基于非支配排序多目标遗传优化算法求解分布式能源的选址与定容。
将可再生能源的分布式发电技术与大电网结 合,是 普 遍 公认的节能减排、绿色 环 保、安全可靠的电力系统运行方式, 是电力发展的方向。分布式电源(DG)是指在一定的地域范围内,以分散方式布置在用户附近, 与环境兼容的小型模块化发电单元,其发电功率为几千瓦到 几十兆瓦。
分布式发电系统目前大多与配电网并网运行。DG 入 电 网后,会对配电网的潮流分布产生影响,进而可以优化配电网 络,缓解配电网输 配 用 电 压 力。但 是 由 于 DG 的 投 入 和 退出有很大的随 机 性,且输出功率的稳定性易受环境影响,因此,DG的不当接入会对电网产生诸多负面影响,如 影 响 配 电网的稳定性及电压质量,产 生 谐 波 等。这 些 影 响 的 大 小 与DG的容量和接入位置有很大关,因此,DG 的选址定容是在 DG规划阶段中需要考虑的重点问题。
由于规划的优化目标较为单一,传 统 的 规 划 方 法 无 法 很 好地解决这一问题。近 年 来,考 虑 电 压、电流质量和环境等因素的多目标优化迅速发展,但量纲的不统一,使得求解的复杂性大大提高,给多目标优化提出了新的挑战。本文在 研究标准粒子群优化算法的基础上,针 对 配 电 网 中 DG 的 选址定容问题,建立了包括有功率损耗、电压质量及接入 DG 的总容量为目标函数的数学模型,运用模糊理论将多目标优化模型转化为基于模糊隶属度的单目标优化模型,并利用非支配排序多目标遗传优化算法进行优化。在IEEE14标准节点测试系统上进行仿真,提出了具有实用价值的 DG配置方案。
功率损耗
电能在从发电端传输到负载端的过程中,输电线路上产生的电能损耗不可址 见,只议r地减小有功功率损耗,提理地配置配电网中的 DG,可以有效地减小有功功率损耗,提高发电利用率,节约能量。基于有功功率损耗的目标函数最优数学表达式为:

电压质量
某些状况下,电力系统在遭受干扰后的几秒或几分钟内,系统中的某些母线电压可能经历大幅度﹑持续性降低,从而使得系统的完整性遭到破坏,功率不能正常地传送给用户。这种灾变称为系统电压不稳定﹐其灾难后果则是电压崩溃。通常用静态电压稳定指标来表示系统电压稳定性。配电网中电
压质量受配电系统的电压稳定性影呵。今乂术用能T网P电压基于期望电压的方差来描述电压质量。基于电压质量的目标函数最优数学表达式为:

DG总容量
在实际应用中不仅要考虑改善电网带来的经济效应,还需要考虑DG安装、运行和维护的成本费用问题。本文中不涉及经济模型,仅考虑接入配电网的DG总容量。基于DG总容量的目标函数最优数学表达式为:

一、分布式能源选址定容问题概述
1. 问题定义与复杂性
分布式能源(DG)选址定容需确定安装位置(节点)与容量大小,是一个典型的多目标优化问题,涉及:
- 多目标冲突:经济性(投资成本、运行维护)、技术性(网损、电压稳定性)、环境性(碳排放、土地占用)目标相互制约。
- 高维约束:包括电网接入容量、电压波动限值、功率平衡方程、地理空间限制等。
- 不确定性因素:可再生能源出力波动(如光伏、风电)、负荷时变特性。
2. 核心挑战
- 解空间庞大:候选位置与容量组合呈指数级增长,传统枚举法失效。
- 目标归一化困难:不同目标量纲差异大(如成本单位vs碳排放单位),需模糊理论或权重法处理。
- 多利益主体协调:需平衡电网公司、DG投资商、环境监管方等多方需求。
二、NSGA-II算法原理与适配性
1. 算法核心机制
NSGA-II通过以下创新解决多目标优化问题:
- 快速非支配排序
将种群按Pareto支配关系分层(Rank 1为最优非支配解集),计算复杂度降至O(MN²),显著提升效率。 - 精英保留策略
合并父代与子代种群,优先保留高质量解,避免优秀基因丢失。 - 拥挤度计算
维持解集多样性,避免收敛至局部最优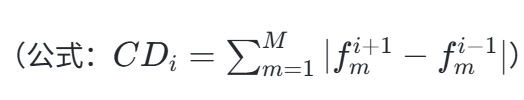
2. 对比传统算法的优势
| 算法类型 | 计算效率 | 解集多样性 | 约束处理能力 |
|---|---|---|---|
| 权重求和法 | 高 | 低(单解) | 弱 |
| NSGA-II | 中高 | 高(Pareto前沿) | 强(支配关系修正) |
| 粒子群优化(PSO) | 中 | 中 | 中 |
NSGA-II通过Pareto前沿提供决策者多方案选择空间,优于单目标算法。
三、选址定容模型构建
1. 决策变量设计
- 位置变量:离散整数(如配电网节点编号)。
- 容量变量:连续实数(DG额定功率,单位kW/MW)。
编码示例:染色体结构
[节点1, 容量1, 节点2, 容量2, ...]。
2. 多目标函数体系
| 目标类别 | 具体指标 | 数学表达式 | 优化方向 |
|---|---|---|---|
| 经济性 | 总成本(投资+运维) | min∑(Cinv+CO&M) | 最小化 |
| 技术性 | 系统网损 | minPloss=∑Ik2Rk | 最小化 |
| 电压偏差指数 | $\min \sum | V_i - V_{ref} | |
| 环境性 | 碳排放量 | min∑(CO2+NOx) | 最小化 |
3. 约束条件建模
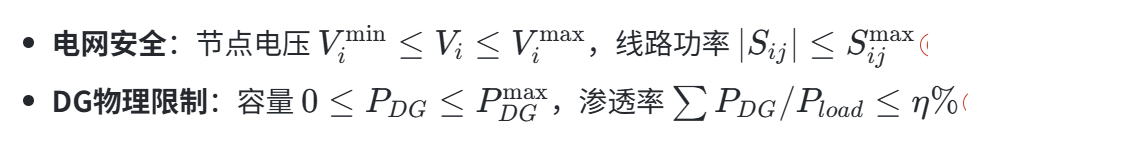
- 地理约束:候选节点需满足空间可接入性(如土地可用性)。
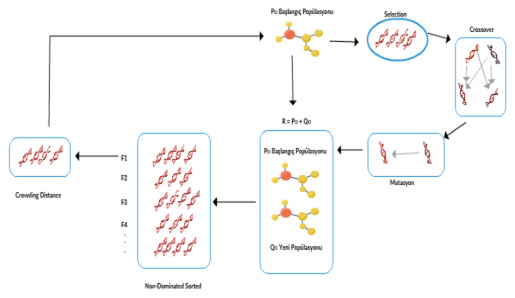
四、NSGA-II算法实现流程
1. 整体流程
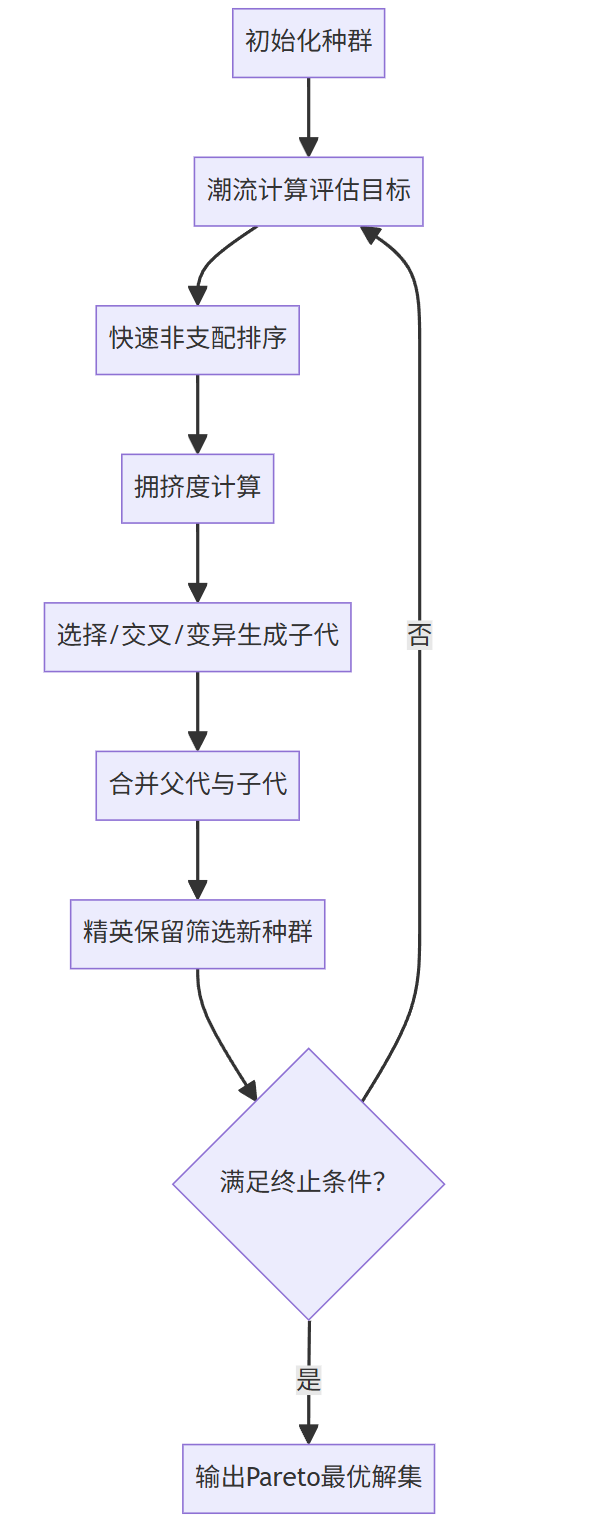
2. 关键步骤详解
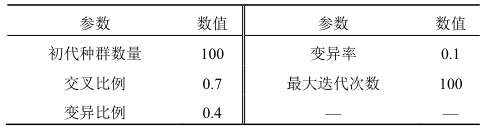
- 种群初始化
- 随机生成DG位置-容量组合,种群规模通常设100–200。
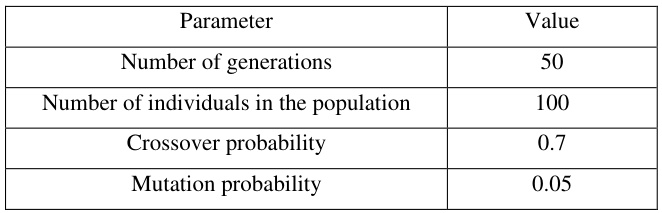
- 随机生成DG位置-容量组合,种群规模通常设100–200。
- 适应度评估
- 调用潮流计算(如牛顿-拉夫逊法)求解网损、电压等指标。
- 遗传操作
- 交叉:模拟二进制交叉(SBX),概率 pc=0.7–0.9。
- 变异:多项式变异,概率 pm=0.05–0.1pm=0.05–0.1 保持多样性。
- 交叉:模拟二进制交叉(SBX),概率 pc=0.7–0.9。
- 环境选择
- 按Rank分层选择,同层按拥挤度降序筛选,确保前沿分布均匀。
五、案例验证与算法性能
1. 典型测试系统结果
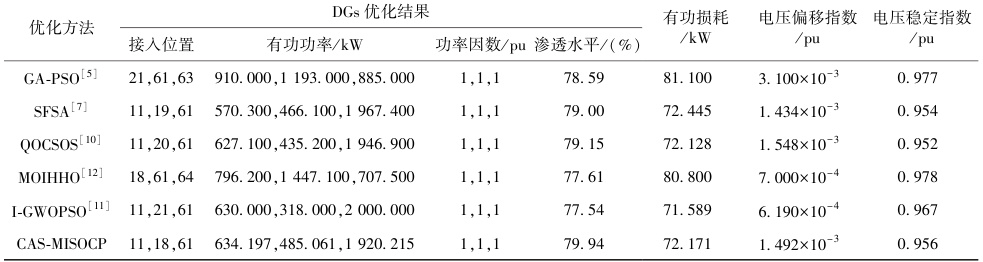
以PG&E69节点系统为例(表:类型1 DG优化结果):
| 优化算法 | 接入位置 | 有功功率(kW) | 网损(kW) | 电压偏移(×10⁻³) |
|---|---|---|---|---|
| GA-PSO | 21,61,63 | 910,1193,885 | 81.10 | 3.10 |
| NSGA-II | 11,18,61 | 495,378,1674 | 4.26 | 1.70 |
| 改进率 | – | – | -94.7% | -45.2% |
NSGA-II网损降低95%,电压稳定性提升45%。
2. 算法性能对比
- 收敛性:在IEEE 33节点系统中,NSGA-II比MOPSO早50代收敛至Pareto前沿。
- 解集质量:拥挤度指标提高30%,解分布更均匀。
- 鲁棒性:在风光出力不确定性场景下,解集标准差降低22%。
六、工程应用与拓展方向
1. 实际应用场景
- 微电网群优化:通过集群划分降低求解维度(如模块度指标)。
- 光储协同规划:以储能日均成本+弃光率为目标,NSGA-III处理高维目标。
- 低碳园区规划:结合碳交易机制,优化DG与能源站协同。
2. 未来研究方向
- 不确定性量化:集成随机规划或鲁棒优化处理风光出力波动。
- 算法融合:NSGA-II+启发式规则(如灵敏度分析)预筛候选节点,减少计算量。
- 动态多目标优化:考虑负荷增长与时变电价,引入滚动优化框架。
📚2 运行结果


部分代码:
%% 雅可比矩阵
J=[jpt jpv; jqt jqv];
X = (inv(J))*M;%偏差
%% 相位偏差
dTh = X(1:nbus-1);
%% 电压偏差
dV = X(nbus:end);
[e1,d1,n1]=eig(JR);%计算矩阵A的特征值和特征向量的函数是eig(A)[V,D,W] = eig(A),[V,D,W] = eig(A)返回满矩阵 W,其列是对应的左特征向量,使得 W’A = DW’。
%diag(A),若A是一个矩阵,则diag函数的作用是产生提取矩阵的对角线;若a是一个向量,则diag函数的作用是产生一个对角线为a的矩阵
%% 目标2 电压稳定性
f2val=max(1./diag((d1)))*max(abs(dQ));%目标2,稳定性
del(2:nbus) = dTh + del(2:nbus);
k = 1;
for i = 2:nbus
if type(i) == 3
V(i) = dV(k) + V(i);
k = k+1;
end
end
%% 目标2和目标3
tval=sum(1./diag((d1)));
po_val=flow_cal(nbus,V,del,BMva);
f1val=sum(po_val);%各支路网损和
f3val=sum(datain(5:8));%DG容量和
fout=[f1val; f2val; f3val];
%% 雅可比矩阵
J=[jpt jpv; jqt jqv];
X = (inv(J))*M;%偏差
%% 相位偏差
dTh = X(1:nbus-1);
%% 电压偏差
dV = X(nbus:end);
[e1,d1,n1]=eig(JR);%计算矩阵A的特征值和特征向量的函数是eig(A)[V,D,W] = eig(A),[V,D,W] = eig(A)返回满矩阵 W,其列是对应的左特征向量,使得 W’A = DW’。
%diag(A),若A是一个矩阵,则diag函数的作用是产生提取矩阵的对角线;若a是一个向量,则diag函数的作用是产生一个对角线为a的矩阵
%% 目标2 电压稳定性
f2val=max(1./diag((d1)))*max(abs(dQ));%目标2,稳定性
del(2:nbus) = dTh + del(2:nbus);
k = 1;
for i = 2:nbus
if type(i) == 3
V(i) = dV(k) + V(i);
k = k+1;
end
end
%% 目标2和目标3
tval=sum(1./diag((d1)));
po_val=flow_cal(nbus,V,del,BMva);
f1val=sum(po_val);%各支路网损和
f3val=sum(datain(5:8));%DG容量和
fout=[f1val; f2val; f3val];
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]周洋,许维胜,王宁,邵炜晖.基于改进粒子群算法的多目标分布式电源选址定容规划[J].计算机科学,2015,42(S2):16-18+31.
[2]冯元元. 基于多目标规划的分布式发电选址定容研究[D].华北电力大学,2015.
[3]杨智君. 基于群智能算法的分布式电源选址与定容[D].太原科技大学,2019.DOI:10.27721/d.cnki.gyzjc.2019.000065.




















 1015
1015

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








