【数据结构】之线段树理解与基础模板

什么是线段树

线段树 是一种通过类似 二分 来实现的一种 二叉树 结构，方便区间的修改与性质的查询，是一种非常节约时间的 数据结构 。

为什么使用线段树

比如我们给你 $N$ 个数，每次可能对其中一个数进行修改，也可能询问区间 $[l,r]$ 中的最大数，那么我们在查询区间中最大值的时候，可以很 $暴力$ 地枚举一边，但这样的话时间复杂度很高，然后这时候我们其实也可以想到 分块 ，用这个方法来存下每个长度为 $m$ 的区间的最大值，修改的时候再看是否有所改变，查询时整块儿整块儿去查询。但是时间复杂度受到块儿的大小以及每次询问时区间的边界与长度等因素的影响，十分不稳定，这时候我们就可以通过 线段树 来解决。

线段树的大致思路

$1.$ 线段树 其实也是通过新建的 数组 来实现，数组 中的每个 节点 代表 原数组 中的一个 区间 。
$2.$ 区间 的长度可能为 $1$ ，当该节点为 最底层的子节点 时，区间 的长度为 $[x,x]$，而 根节点代表的区间长度 为 $N$ ，即 根节点 代表整个数组 $[1,N]$ 的一种性质。
$3.$ 对于每个 不是底层的节点 ，假设其包含区间为 $[l,r]$，则其 左子结点 代表 $[l,mid]$ ，右子节点 代表 $[mid+1,r]$ ，其中 $mid=(l+r)>>1$。
$4.$ 若某节点在 线段树数组 中的下标为 $x$ ，则其子节点在 线段树数组 中的下标分别为 $x\ast 2$ 和$x\ast 2+1$，有时我们也可以用位运算表示，分别为 $x<<1$ 和 $x<<1|1$ 。

当我们用区间表示时：

---

基础代码模板

我们这里以单点修改，区间查询最大值为例子。

线段树的声明

struct ST{int l , r , dat ;} t[N * 4];
//l和r分别表示该节点所代表区间的左右边界，dat该区间内的最大值 

线段树的建树

void build(int p , int l , int r)
{
	t[p].l = l; t[p].r = r;//记录该节点所表示的区间 
	if(l == r){return;}//此时说明是最底部节点 
	int mid = (l + r) / 2 ;
	build(p * 2 , l , mid);//建立左子结点 
	build(p * 2 + 1 , mid + 1 , r);//建立右子节点 
	t[p].dat = max(t[p * 2].dat , t[p * 2 + 1].dat);//更新区间内的最大值 
}

前文说过线段树有些 分治 的思想，那么其实也就离不开 递归 ，我们在建树的过程中相当于不断递归区间直到最底部的节点，然后向上 $return$ 来更新该区间内的最大值。

单点修改

void add(int p,int x,int v)
{
	if(t[p].l == t[p].r){t[p].dat = v ; return ;}//到达最底部节点 
	int mid = (t[p].l + t[p].r) / 2;
	if(x <= mid) add(p * 2 , x , v);//若要修改的点在该节点的左子节点 
	else add(p * 2 + 1 , x , v);//若...在右子节点 
	t[p].dat = max(t[p * 2].dat , t[p * 2 + 1].dat);//更新修改后区间的最大值 
}

区间查询最大值

int ask(int p , int l , int r)
{
	if(l <= t[p].l && r >= t[p].r) return t[p].dat;//若当前查询到的区间在询问区间范围内 
	int mid = (t[p].l + t[p].r) / 2;
	int val = -(1 << 30);
	if(l <= mid) val = max(val , ask(p * 2 , l , r));//若该区间左子结点与查询区间有重叠 
	if(r > mid) val = max(val , ask(p * 2 + 1 , l , r));//...右子节点...
	return val;//val记录该区间内的最大值，最终返还 
}

主函数中的调用

build(1 , 1 , n);//分别代表该节点在当前数组中的下标，所表示区间的左端点与右端点
add(1,b,c);//从1号节点开始，即从根节点开始，将第b个数改为c
ans = ask(1,b,c)//从1号节点开始查询，区间的左右端点分别为 b 和 c 

---

洛谷P3372 【模板】线段树 1

题目描述

如题，已知一个数列 { a i } \{a_i\} {ai​}，你需要进行下面两种操作：

1. 将某区间每一个数加上 $k$。
2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数 $a_i$，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

1. 1 x y k：将区间 $[x,y]$ 内每个数加上 $k$。
2. 2 x y：输出区间 $[x,y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例 #1

输入 #1

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出 #1

11
8
20

说明/提示

对于 $15\%$ 的数据：$n\le 8$，$m\le 10$。
对于 $35\%$ 的数据：$n\le {10}^3$，$m\le {10}^4$。
对于 $100\%$ 的数据：$1\le n,m\le {10}^5$，$a_i,k$ 为正数，且任意时刻数列的和不超过 $2\times 10^{18}$。

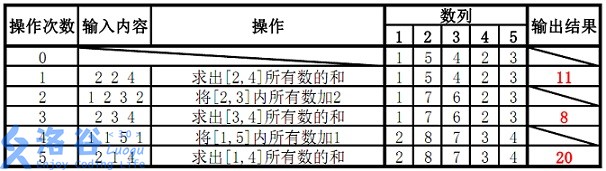
【样例解释】

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define N 100010
int n , m , a[N] , x , y , k , op , sum[N << 2] , jia[N << 2] ;
void build(int p , int x , int y)
{
	if(x == y) {sum[p] = a[x] ; return ;}
	int mid = (x + y) >> 1 ;
	build(p << 1 , x , mid) ;
	build(p << 1 | 1 , mid + 1 , y) ;
	sum[p] += sum[p << 1] + sum[p << 1 | 1] ;
}
void spread(int p , int x , int y)
{
	if(jia[p])
	{
		int mid = (x + y) >> 1 ;
		sum[p << 1] += jia[p] * (mid - x + 1) ;
		sum[p << 1 | 1] += jia[p] * (y - mid) ;
		jia[p << 1] += jia[p] ; jia[p << 1 | 1] += jia[p] ;
		jia[p] = 0 ;
	}
	return ;
}
void add(int p , int x , int y , int l , int r , int d)
{
	if(l <= x && r >= y)
	{
		sum[p] += d * (y - x + 1) ;
		jia[p] += d ;
		return ;
	}
	spread(p , x , y) ;
	int mid = (x + y) >> 1 ;
	if(l <= mid) add(p << 1 , x , mid , l , r , d) ;
	if(r > mid) add(p << 1 | 1 , mid + 1 , y , l , r , d) ;
	sum[p] = sum[p << 1] + sum[p << 1 | 1] ;
	return ;
}
int ans(int p , int x , int y , int l , int r)
{
	if(l <= x && r >= y) return sum[p] ;
	spread(p , x , y) ;
	int mid = (x + y) >> 1 , val = 0 ;
	if(l <= mid) val += ans(p << 1 , x , mid , l , r) ;
	if(r > mid) val += ans(p << 1 | 1 , mid + 1 , y , l , r) ;
	return val ;
}
signed main()
{
	scanf("%lld%lld" ,&n ,&m) ;
	for(int i = 1 ; i <= n ; i ++)
	{
		scanf("%lld" ,&a[i]) ;
	}
	build(1 , 1 , n) ;
	while(m --)
	{
		scanf("%lld" ,&op) ;
		if(op == 1)
		{
			scanf("%lld%lld%lld" ,&x ,&y ,&k) ;
			add(1 , 1 , n , x , y , k) ;
		}
		if(op == 2)
		{
			scanf("%lld%lld" ,&x ,&y) ;
			printf("%lld\n" ,ans(1 , 1 , n , x , y)) ;
		}
	}
	return 0 ;
}

优化代码结构与习惯，使用 数组 传递信息而不是 结构体 ，每个节点左右儿子的下标在 递归 的过程中传递，这样在 build 的时候就也不用处理左右儿子的下标问题了。

我们注意到这个题目是区间修改，需要上懒标记

如何理解懒标记呢？
打个比方你需要把区间 $[l,r]$ 的数都加上 $x$ ，那么你先在能表示这个区间的点都加上这个 懒标记 ，记作 jia[p] ，比如一个点表示的区间是 $[l,r]$ ，那么这个点求和的时候就要加上 $(r-l+1)\ast jia[p]$ ，并且将这个懒标记下传，让 jia[p << 1] += jia[p] 和 jia[p <<1 | 1] += jia[p] 。

---

注

线段树 的 数组 要开 $4$ 倍
简单基础的题可以看另一篇博客【数据结构】之树状数组与线段树的咋题题面加代码不解释