The-Design-and-Analysis-of-Algorithms 作业5

1. 问题

n个点在公共空间中，求出所有点对的欧几里得距离最小的点对。

2. 解析

令P为笛卡儿平面上n>1个点构成的集合。简单起见，假设集合中的每个点都不一样，这些点是按照其x、y轴坐标升序排列的，并将这个列表示为 Q。

当2≤n≤3时，问题就可以通过蛮力算法求解。
当n>3时可以利用点集在x轴方向上的中位数m，在该处作一条垂线，将点集分成大小分别为⌈n/2⌉和⌊n/2⌋的两个子集Pl和Pr。即使得其中⌈n/2⌉个点位于线的左边或线上，⌊n/2⌋个点位于线的右边或线上。然后就可以通过递归求解子问题Pl和Pr来得到最近点对问题的解。其中dl和dr,分别表示在Pl和Pr中的最近对距离，并定义d =min {dl,dr}。
可以只关注以分割带为对称的、宽度为2d的垂直带中的点，因为任何其他点对的距离都至少为d。

设S是来自Q，位于分割线2d宽度范围内的垂直带的点的列表。由于的特点，因此S是按照y轴坐标升序排列的。我们扫描该列表，当遇到更近的点对时，更新目前为止的最小距离dmin。

3. 设计

EfficientClosest Pair(P,Q)
//输入 ：数组P存n≥2个点，按其x轴坐标升序排序；
数组Q存和P相同的点，按其y轴坐标升序排序；
//输出：最近点对之间的欧几里得距离；

if n≤3
返回蛮力算法求出dmin；
else
将P的前半部分(n/2)个点复制到P1，Q的前半部分(n/2)个点复制到Q1中；
将P的余下部分(n/2)个点复制到Pr，Q的余下部分(n/2)个点复制到Qr中；
d1←EfficientClosest Pair(P1,Q1)
dr←EfficientClosest Pair(Pr,Qr)
d←min{d1,dr}
m←P[前半部分(n/2)-1].x
将Q中所有绝对值（x-m）<d的点复制到数组S[0…num-1]
dmin=sqrt((y2-y1)(y2-y1)+(x2-x1)(x2-x1))
dminsq←dd
for i←0 to num-2 do
k←i+1
while k≤num-1 and (S[k].y-S[i].y)(S[k].y-S[i].y)<dimsq
dminsq←min((S[k].x-S[i].x)2+(S[k].x-S[i].x)2),dminsq)
k←k+1
return sqrt(dminsq)

4. 分析

在分解和合并时，可能存在按照x轴、y轴进行排序的预处理O(nlogn)，该问题在解决阶段只做提取的操作为Θ(n)，递推式为：

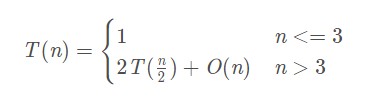
计算后得到整体时间复杂度为： O(nlogn)

5.源码

https://github.com/LiChunning/The-Design-and-Analysis-of-Algorithms/blob/main/%E6%9C%80%E8%BF%91%E5%AF%B9%E9%97%AE%E9%A2%98.cpp