8.9 约数个数与约数之和

约数个数

对于一个正整数N，他的约数个数d(N) = N所有的质因数的指数+1后的乘积
例：求12的约数个数
解
先对12分解质因数，得到2 2 3，即$2^2+3^1$。
2的指数个数为2，3的指数个数为2，根据公式可得$d(12)=(2+1)\ast (1+1)=6$

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=1005;

unordered_map<int, int> primes;//哈希表，元素排列无序 

void find(int n)
{
	int cnt=0;
	for(int i=2;i<=n/i;i++)
	{
		while(n%i==0)
		{
			n /=i;
			primes[i]++;
		}
	}
	if(n>1)
	{
		primes[n]++;
	}
	return;
}

int main()
{
	int n;
	cin>>n;
	find(n);
	
	int res = 1;
	for(auto t:primes) res=(res*(t.second+1));//公式 
	
	cout<<res;
	return 0;
	
} 

---

约数之和

首先，对于一个大于1的正整数N，我们可以把它表示成：

N = $p_1^{a1}$ * $p_2^{a2}$ * $p_3^{a3}$ * … * $p_k^{ak}$。

再根据上面所学的，

N的约数个数一共有 $d(n)=(p_1+1)(p_2+1)(p_3+1)...(p_k+1)$个。

实际上，N的约数个数是由$p_1^{a1}$ ，$p_2^{a2}$ ， $p_3^{a3}$…每一个数的约数挑一个相乘得来，一共有 $(p_1+1)(p_2+1)(p_3+1)...(p_k+1)$种挑法，所以约数和即：

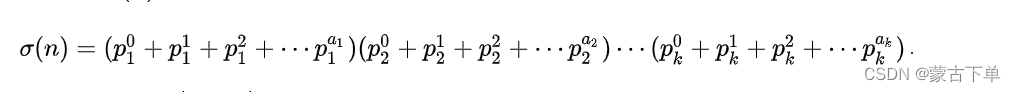
也可以表示为

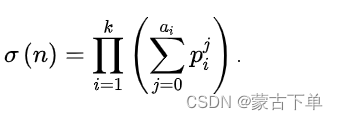
举例：求360的约数和。
解
将360分解质因数可得
360 = 2 2 2 3 3 5
由约数和定理可知，360所有正约数的和为
$(2^0+2^1+2^2+2^3)\times (3^0+3^1+3^2)\times (5^0+5^1)$
$=(1+2+4+8)(1+3+9)(1+5)=15\times 13\times 6=1170$

代码实现

#include<bits/stdc++.h>
using namespace std;
unordered_map<int,int> primes;

void find_2(int x){
    for(int i = 2;i <= x/i;i++){
        if(x % i==0){
            while(x % i == 0){
                primes[i]++;
                x /= i;
            }
        }
    }
    if(x > 1) primes[x]++; 
}

int main()
{
	int n;
	cin>>n;
	find_2(n);
	    
    int res = 1;
    for(auto t:primes){
    	int a = t.first,b = t.second;//first是底数，second是指数 
    	int p = 1;
    	while(b--)
    	{
    		p = (p*a+1);//代入公式，求每一个质因子的约数和 
		}
		res *= p;//将每一个质因子的求和再乘起来 
    }
    cout<<res;
}