8.27 矩阵乘法

我只是一个可怜的小女孩，为什么要让我接触线性代数（阴暗地爬走

矩阵的概念

定义

矩阵，数学术语。在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。通俗的来说，由$m\ast n$个数组成的$m\ast n$大小的数表，称为一个矩阵。

名词解释

同型: 两个矩阵行数相同，列数也相同。

秩：一个矩阵A的列秩是A的线性独立的纵列的极大数，一般表示为$r(A)$。

等价: 同型矩阵，并且秩相等

相等: 同型矩阵，并且对应元素都相等

---

矩阵乘法

矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数（column）和第二个矩阵的行数（row）相同时才有意义。 一般单指矩阵乘积时，指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。由于它把许多数据紧凑地集中到了一起，所以有时候可以简便地表示一些复杂的模型，如电力系统网络模型。

因此，给出如下解释：
令矩阵$A$ = $m\ast n$, 若矩阵A与矩阵B可相乘，则矩阵$B$= $n\ast k$, $k$为任意实数。

变换方式

变换的方式，就是用A的每一行，去乘以B的每一列。

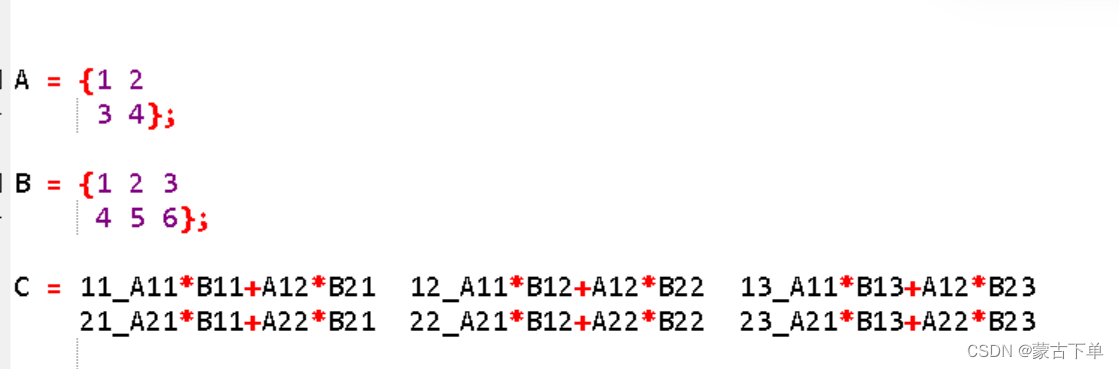
解释：

$11-A11\ast B11+A12\ast B21$

矩阵$C[1,1]$存储的，是$A[1,1]\ast B[1,1]+A[1,2]\ast B[2,1]$。

具体的可以看视频：

矩阵乘法

变换本质

物理学上，它的本质之一是对空间的基向量进行旋转，剪切等操作。
数学上，它可以用于解m个方程n个未知数的线性方程组。
（对我来说，这个比较好理解，当然也有其他的解释。）

例题

AcWing883 高斯消元解方程组

核心代码

const int N=110;

const double eps=1e-8;

int n;

double a[N][N];

int gauss(){

    int c,r;

    for (c=0,r=0;c<n;c++){

        int t=r;

        for(int i=r;i<n;i++){  //筛选出所在列元素最大的行
            if(fabs(a[i][c])>fabs(a[t][c])) t=i;
        }

        if(fabs(a[t][c])<eps) continue;  //正对角线中有元素为0,这时有无穷解和无解

        if(t!=r) for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);  //若t改变，则交换两行

        for(int i=n;i>=c;i--) a[r][i]/=a[r][c];  //将所在行所在列元素变为1

        for(int i=r+1;i<n;i++){  //将所在行所在列的下方的行的所在列元素变为0
            if(fabs(a[i][c])>eps){
                for(int j=n;j>=c;j--) a[i][j]-=a[r][j]*a[i][c];
            }
        }

        r++;

    }

    if(r<n){  //row<n,即对角线中元素为0的行未被算上
        for(int i=r;i<n;i++){
            if(fabs(a[i][n])>eps) return 2;
        }
        return 1;
    }

    for(int i=n-1;i>=0;i--){  //将非主元位置的A系数矩阵的其他x消去
        for(int j=i+1;j<n;j++) a[i][n]-=a[j][n]*a[i][j];
    }

    return 0;

}