PAT (Advanced Level) Practice - 1119 Pre- and Post-order Traversals（30 分）

题目链接：点击打开链接

题目大意：给出一棵树的结点个数n，以及它的前序遍历和后序遍历，输出它的中序遍历，如果中序遍历不唯一就输出No，且输出其中一个中序即可，如果中序遍历唯一就输出Yes，并输出它的中序。

解题思路：用 only 标记是否唯一，如果为 1 就表示中序是唯一的。
已知二叉树的前序和后序是无法唯一确定一颗二叉树的，因为可能会存在多种情况，这种情况就是一个结点可能是根的左孩子也有可能是根的右孩子，如果发现了一个无法确定的状态，置 only= 0，又因为题目只需要输出一个方案，接下来的问题是如何求根结点和左右孩子划分的问题了，前序的开始的第一个应该是后序的最后一个是相等的，这个结点就是根结点，以后序的根结点的前面一个结点作为参考，寻找这个结点在前序的位置，就可以根据这个位置来划分左右孩子，递归处理。如果一直可以明确划分，则唯一，否则有多种情况。

AC 代码

#include<bits/stdc++.h>
#include<cmath>

#define mem(a,b) memset(a,b,sizeof a)
#define ssclr(ss) ss.clear(), ss.str("")
#define INF 0x3f3f3f3f
#define MOD 1000000007

using namespace std;

typedef long long ll;

int pre[40], post[40], only, cnt, n;

struct node
{
    int d,l,r;
}T[40];

int create(int l1,int r1, int l2,int r2) // pre post
{
    if(l1>r1) return -1;

    int rt=r2;
    int p1=l1+1,p2;

    // p1<=r1 一定要加，否则当出现l2==r2时，r2根本没有前面的结点了，使得p1越界导致下面都出问题
    while(p1<=r1 && pre[p1]!=post[rt-1]) p1++;
    p2=p1-l1;

    T[rt].d=post[rt];
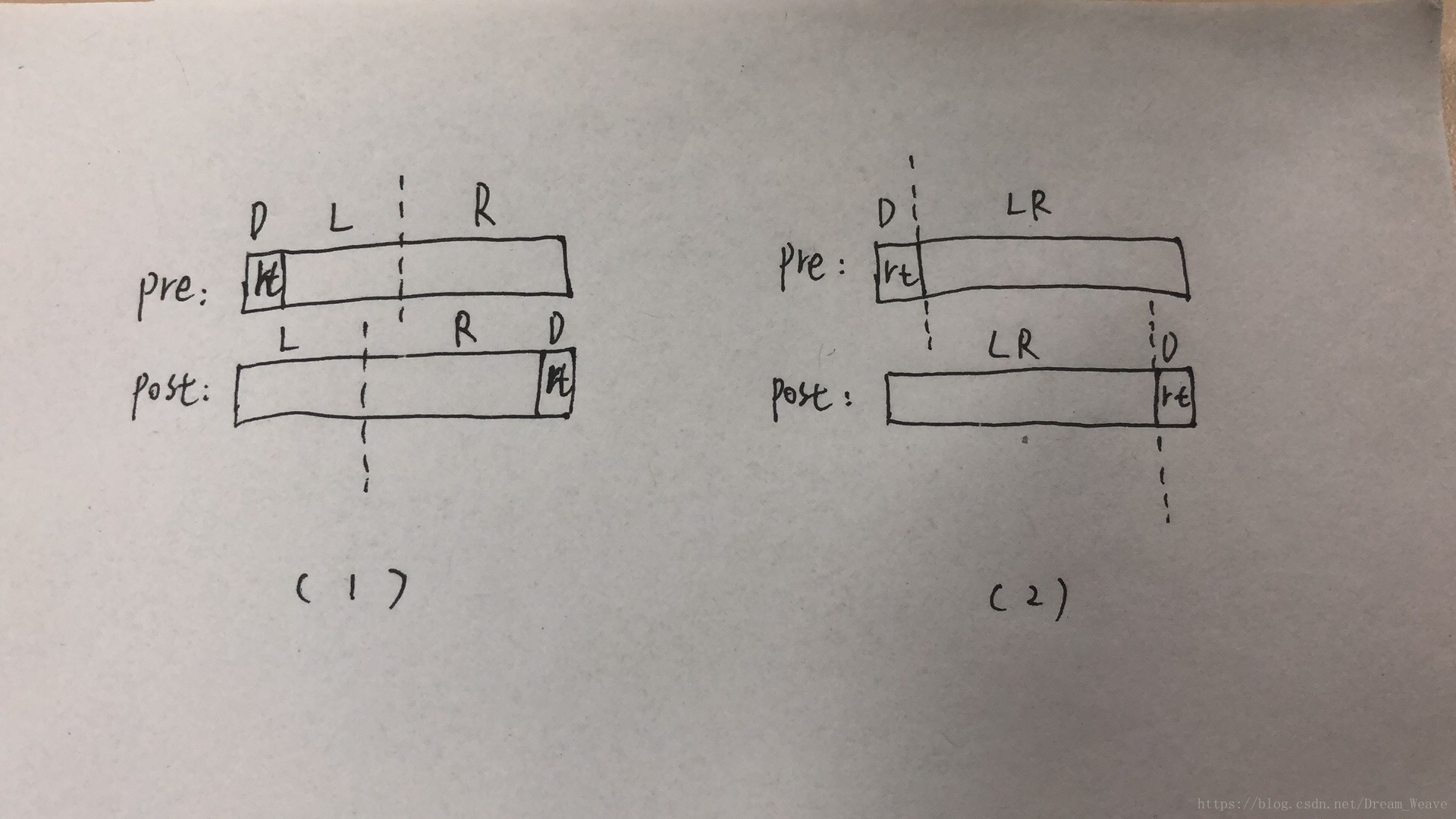
    // p2>1 如图所示，图1是正常情况(有明确的分界线可判断左右子树的位置)，图2是这里避免出现的情况(无明确分界线使得左右子树的位置有多种情况)
    if(p2>1) T[rt].l=create(l1+1,p1-1,l2,l2+p2-1-1);
    else if(l1==r1) T[rt].l=-1;                     // l1==r1 需要终止左孩子
    else if(l1!=r1) only=0, T[rt].l=-1;             // 说明遇到了图2情况
    T[rt].r=create(p1,r1,l2+p2-1,r2-1);

    return rt;
}

void inT(int rt)
{
    if(rt==-1) return;
    inT(T[rt].l);
    printf("%d%c",T[rt].d,++cnt==n?'\n':' ');
    inT(T[rt].r);
}

int main()
{
    int rt;
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&pre[i]);
    for(int i=0;i<n;i++) scanf("%d",&post[i]);
    only=1;
    rt=create(0,n-1,0,n-1);
    puts(only?"Yes":"No");
    inT(rt);

    return 0;
}