2024亚太杯数学建模竞赛（中文赛项）B题学习

最新推荐文章于 2025-07-11 17:47:22 发布

DesolateGIS

最新推荐文章于 2025-07-11 17:47:22 发布

阅读量588

点赞数 4

CC 4.0 BY-SA版权

分类专栏：数学建模文章标签：数学建模学习

本文链接：https://blog.youkuaiyun.com/DesolateGIS/article/details/145861655

数学建模专栏收录该内容

17 篇文章

订阅专栏

一、寻找强相关性特征

简述

Pearson相关系数是衡量两个数据集合是否在一条线上面，用于衡量变量间的线性关系

用Pearson相关性分析模型计算出各指标与洪水发生概率的相关性系数，相关性系数越高的与洪水发生概率的相关性越大。

由于各指标与洪水发生概率的相关性系数很接近，采用特征组合的方法形成复合特征增强模型的预测能力。

建立随机森林模型评估特征的重要性，准确识别出对洪水预测影响最大的因素：

1.首先采取自助采样法进行样本选择。

先随机取出一个样本放入采样集中，再把该样本放回初始数据集中，使得下次采用时该样本扔有可能被选中，这样经过多次随机采样操作，我们得到含有全部样本的采样集，初始数据集中有的样本多次出现，有的则从未出现。

最终，初始数据集中约有36.8%的样本未出现在采样数据集中

初始数据集中约有 63.2％的样本出现在采样数据集中

2.进行特征选择。

在决策树的每个分裂点，随机选择特征的一个子集为每次分裂时考虑的特征数。

3.递归构建决策树并计算特征重要性，找到特征重要性最大的指标为与洪水发生概率具有强相关性的指标。

代码

clear
clc

% 读取train.csv文件，保留原始列标题
data = readtable('train.csv', 'VariableNamingRule', 'preserve');

% 提取指标列（从第二列到倒数第二列）和洪水发生概率（最后一列）
x = data(:, 2:end-1);
y = data{:, end};

% 定义特征组合
% 组合特征1: 淤积损失 + 湿地损失
combine_feature1 = x{:, '淤积'} + x{:, '湿地损失'};

% 组合特征2: 气候变化 + 农业实践
combine_feature2 = x{:, '气候变化'} + x{:, '农业实践'};

% 组合特征3: 地形排水 + 城市化 + 政策因素
combine_feature3 = x{:, '地形排水'} + x{:, '城市化'} + x{:, '政策因素'};

% 计算新特征与洪水发生概率的相关性
correlation1 = corr(combine_feature1, y);
correlation2 = corr(combine_feature2, y);
correlation3 = corr(combine_feature3, y);


% 绘制相关系数柱状图
figure;
%使用bar函数绘制柱状图
bar([correlation1; correlation2; correlation3]);
% 使用set函数修改当前axes对象(gca)的属性
%设置了XTickLabel属性来指定X轴刻度标签,通过XTick属性设置X轴刻度的位置;1:3指定了这三个标签在X轴上的位置
set(gca, 'XTickLabel', {'组合特征1', '组合特征2', '组合特征3'}, 'XTick', 1:3);


% 用散点图表示组合特征与洪水发生概率的关系
figure;
%循环遍历三个不同的组合特征，针对每个特征绘制了一个散点图，并在同一窗口中以子图的形式呈现出来
for i = 1:3
    %subplot函数创建一个1行3列的子图阵列，第i个位置准备绘图
    subplot(1,3,i);
    %绘制散点图，eval函数将字符串转换为matlab可执行语句，分别表示散点图的横纵坐标
    %'filled'参数表示散点是实心的
    scatter(eval(['combine_feature', num2str(i)]), y, 10, 'filled');
end

运行结果

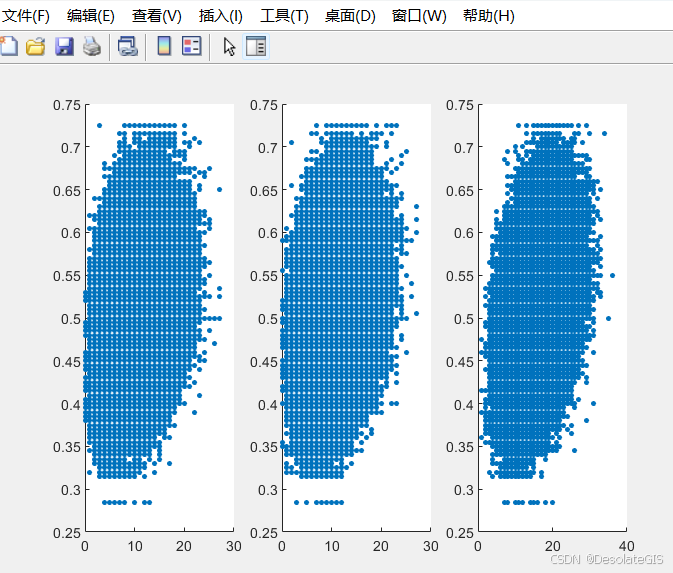
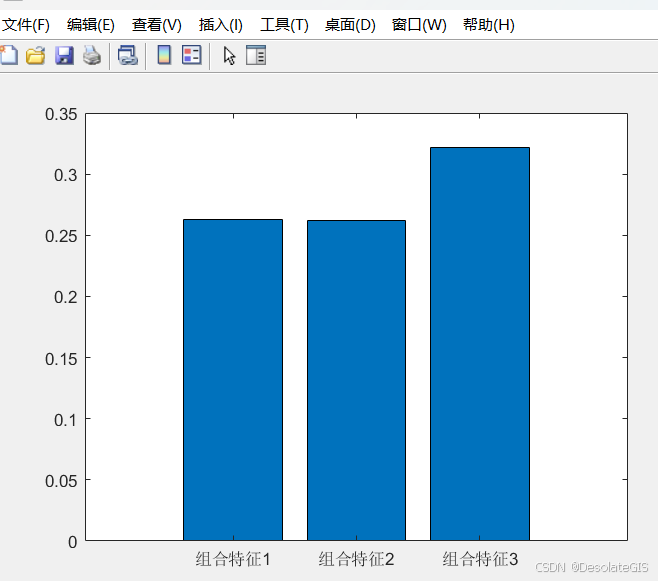
二、、绘图

环形图

clear
clc
% 数据
data = [15, 30, 45]; % 各个部分的数据
labels = {'A', 'B', 'C'}; % 标签

% 创建饼图
figure;
h = pie(data);

% 添加中心圆，创造环形效果
hold on;
theta = linspace(0, 2*pi);
x_center = cos(theta) * 0.7; % 调整0.7改变内圆大小
y_center = sin(theta) * 0.7;
fill(x_center, y_center, 'w'); % 选择白色填充

%确保X轴和Y轴的比例相同，保持图形的真实比例
axis equal;
%为图表添加图例，并自动选择最佳位置来放置图例
legend(labels, 'Location', 'best');

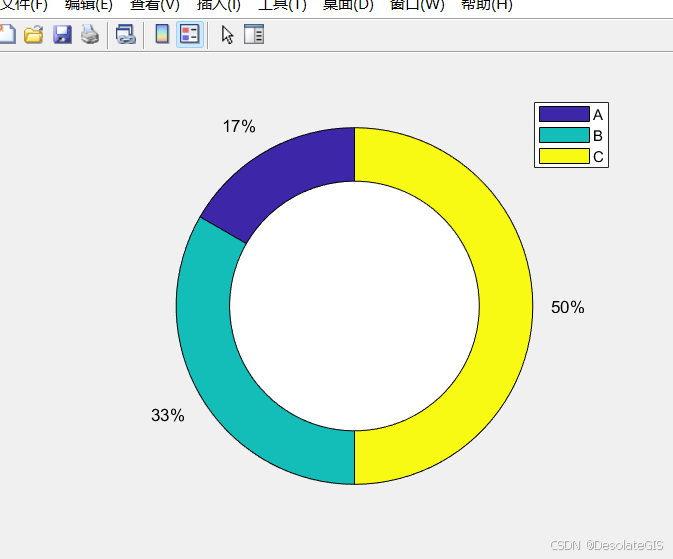
箱型图

clear
clc

% 生成一些示例数据
m = 5; % 数据集数量
n = 100; % 每个数据集中的样本数量
data = zeros(n, m); % 初始化数据矩阵

for i = 1:m
     % 为每个数据集生成正态分布随机数
    data(:, i) = normrnd(5+i, 1, [n, 1]);
end

% 绘制箱线图
figure;
boxplot(data);

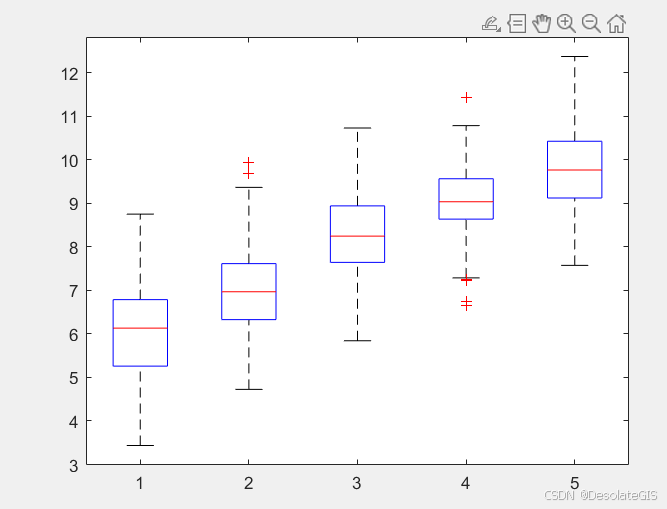
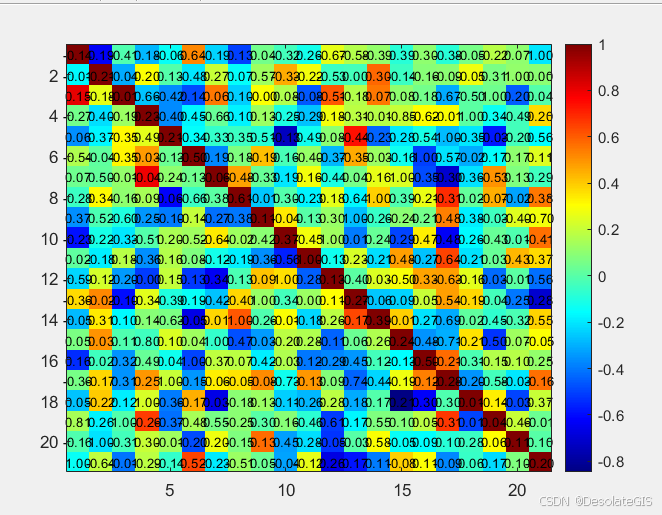
热力图

clear
clc

% 生成一些示例数据
m = 21; % 数据集数量
data = zeros(m, m); % 初始化数据矩阵

% 填充数据矩阵
for i = 1:m
    for j = 1:m
        if i == j
            data(i, j) = 1.0; % 对角线元素为1.0
        else
            % 使用正态分布生成其他元素的数据
            data(i, j) = normrnd(0, 0.3); % 平均值为0，标准差为0.3
            % 将数据限制在[-1, 1]范围内
            data(i, j) = max(min(data(i, j), 1), -1);
        end
    end
end

% 绘制热力图
figure;
imagesc(data);
colorbar; % 添加颜色条

% 设置颜色映射
colormap(jet); % 使用jet颜色映射

% 添加数值标签
for i = 1:m
    for j = 1:m
        text(j, m-i+1, num2str(data(i, j), '%.2f'), 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle', 'FontSize', 8);
    end
end

梯形图

用PowerPoint绘制该图