一、问题简述
TSP问题(旅行商问题)是指旅行家要旅行n个城市,要求各个城市经历且仅经历一次然后回到出发城市,并要求所走的路程最短。
下面用蚁群算法解决该问题。
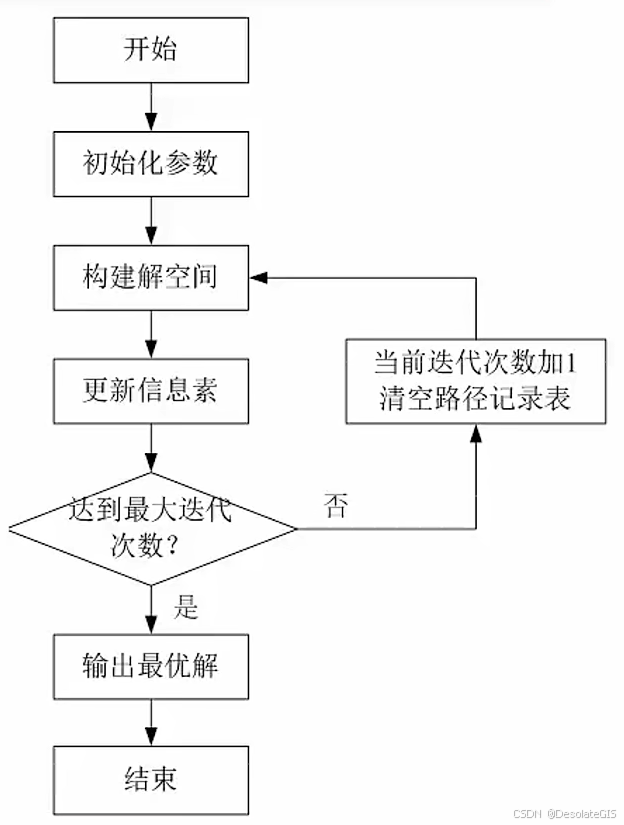
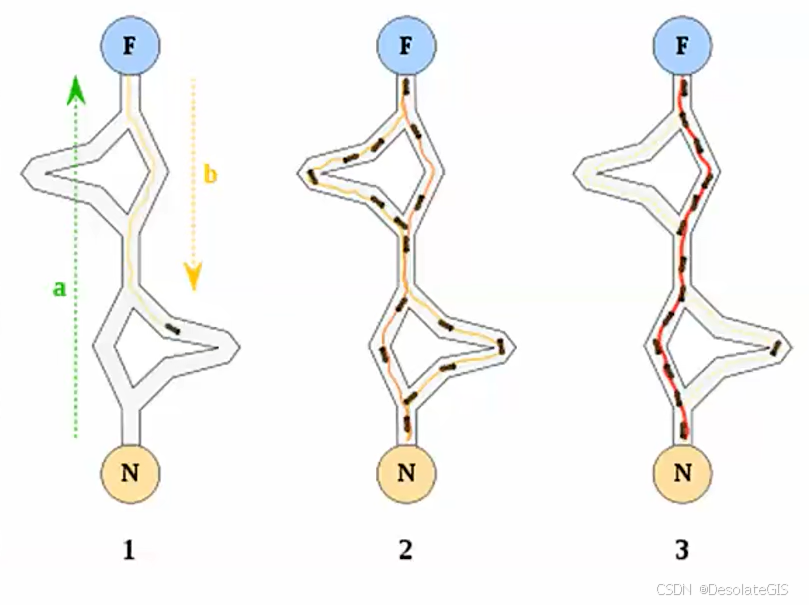

二、代码
clear
clc
%读取xlsx文件
point = readmatrix("ACA_data.xlsx");
%城市数量
n = height(point);
%各个城市之间距离的邻接矩阵
D = ones(n, n);
%计算各城市间距离的邻接矩阵
for i = 1 : n
for j = 1 : n
D(i, j) = sqrt((point(i, 1) - point(j, 1)) ^2 + (point(i, 2) - point(j, 2)) ^2);
end
end
%蚁群数量
m = 50;
%迭代次数
G = 100;
%信息素重要程度因子
alpha = 0.5;
%信息素挥发因子
rho = 0.3;
%启发因子
beta = 0.5;
%信息素常量
Q = 2;
%启发函数
Eta = 1./D;
%各个城市之间信息素的邻接矩阵
Tau = ones(n, n);
%路径记录
Table = zeros(m, n);
%记录历代蚁群的最小距离
distance_pop = inf;
%记录最小距离路径
Min_route = zeros(1, n);
%记录每代蚁群的最小距离
distance_now_pop = zeros(G, 1);
%初始化城市编号
city_index = 1 : n;
for i = 1 : G
%随机蚁群中每个个体的初始城市
Table(:, 1) = randi([1, n], 1, m);
%对城市循环选择路径
for j = 2 : n
%记录访问过的城市编号
tabu = Table(:, 1 : (j - 1));
%初始化未访问城市编号矩阵
allow = zeros(m, n - j + 1);
for k = 1 : m
%记录未访问城市位置矩阵
allow_index = ~ismember(city_index, tabu(k, :));
%由位置矩阵得到未访问过的城市编号
allow(k, :) = city_index(allow_index);
end
%计算城市转移概率
p = allow;
for k = 1 : m
for l = 1 : length(allow(1, :))
p(k, l) = Tau(tabu(k, end), allow(k, l)) .^ alpha .* Eta(tabu(k, end), allow(k, l)) .^ beta;
end
p(k, :) = p(k, :) / sum(p(k, :));
end
%cumsum函数表示对前缀进行累加
Cs = cumsum(p, 2);
%轮盘赌确定下一步选择哪个城市
for k = 1 : m
temp_index = find(Cs(k, :) > rand);
Table(k, j) = allow(k, temp_index(1));
end
end
%记录当前代每个个体的移动总距离
distance_per = zeros(m, 1);
for k = 1 : m
for l = 2 : n
distance_per(k) = distance_per(k) + D(Table(k, l), Table(k, l - 1));
end
distance_per(k) = distance_per(k) + D(Table(k, end), Table(k, 1));
end
%计算历代蚁群的移动距离最小值及路径
[distance_now_pop(i), min_distance_index] = min(distance_per);
if distance_now_pop(i) < distance_pop
distance_pop = distance_now_pop(i);
Min_route = Table(min_distance_index, :);
end
%初始化信息素变化量矩阵
Delta_Tau = zeros(n, n);
for k = 1 : m
%计算当前代各城市之间的信息素变化值
for j = 2 : n
Delta_Tau(Table(k, j - 1), Table(k, j)) = Delta_Tau(Table(k, j - 1), Table(k, j)) + Q / distance_per(k);
end
Delta_Tau(Table(k, n), Table(k, 1)) = Delta_Tau(Table(k, n), Table(k, 1)) + Q / distance_per(k);
end
%更新信息素
Tau = Tau * (1 - rho) + Delta_Tau;
%取出最优路径经过的点位
tempx_plot = point(Min_route, 1);
tempy_plot = point(Min_route, 2);
%将最优路径经过的点位的行列数倒置,确保与后面要拼接的矩阵保持相同行数,进而进行列拼接
x_plot = [tempx_plot.', [point(Min_route(1), 1)]];
y_plot = [tempy_plot.', [point(Min_route(1), 2)]];
%绘制各城市点位与最短路径
plot(x_plot, y_plot, 'b--', x_plot, y_plot, 'r*' );
title(['第', num2str(i), '次迭代']);
pause(0.5);
end
三、运行结果
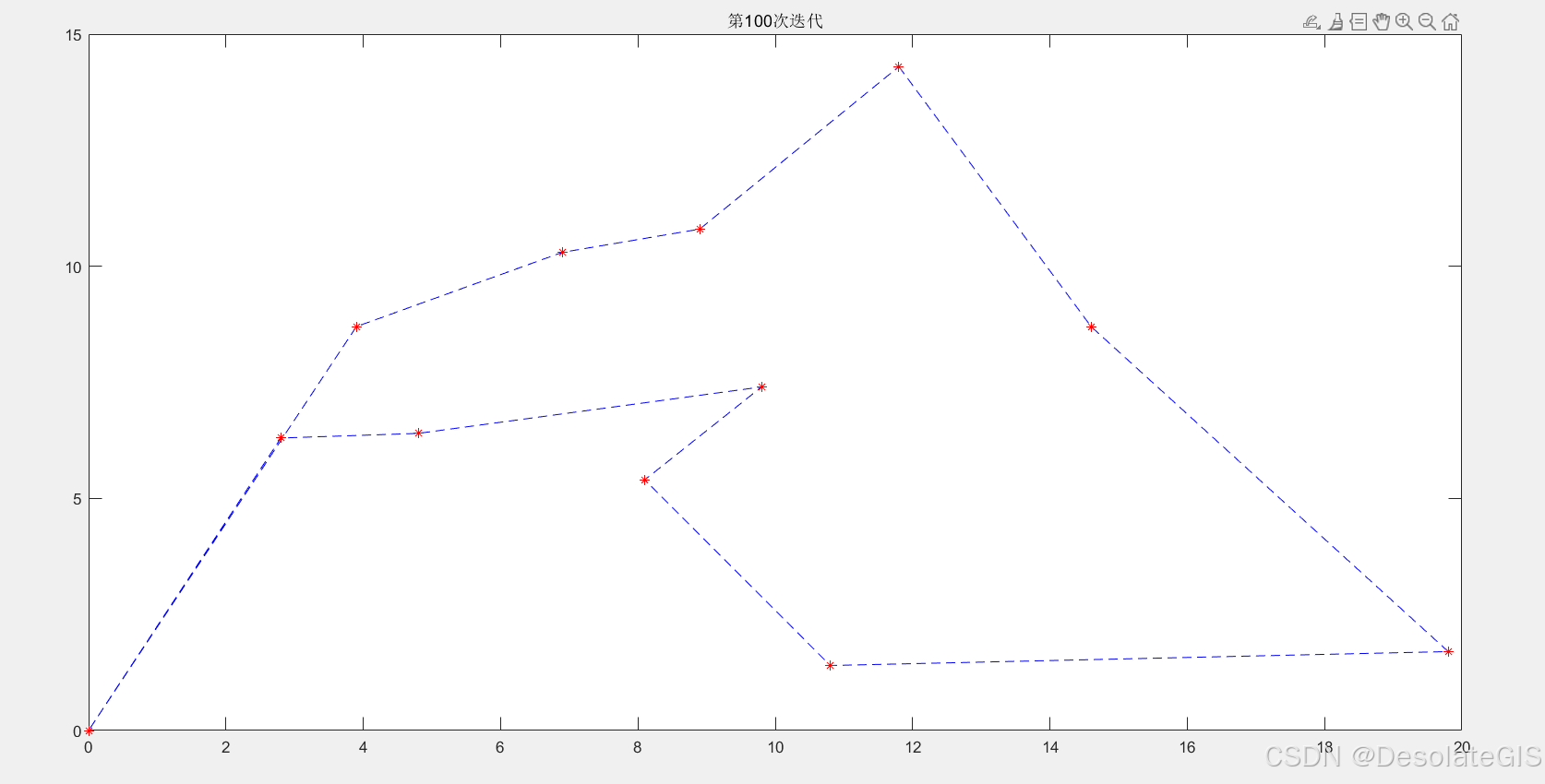





















 1812
1812

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








