一、问题简述
TSP问题(旅行商问题)是指旅行家要旅行n个城市,要求各个城市经历且仅经历一次然后回到出发城市,并要求所走的路程最短。
下面用模拟退火算法解决该问题。
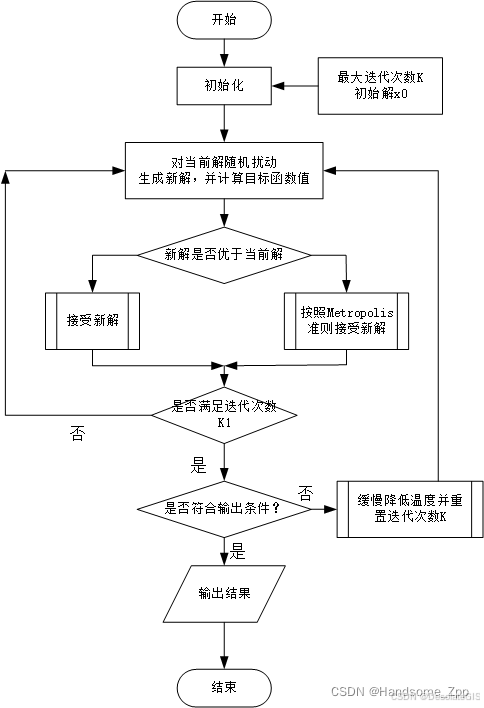
二、代码
1.主函数
clear
clc
point = [0, 0;
2, 4;
3, 5;
1, 1;
5, 7;
8, 2;
18, 6;
19, 1]; %初始化各城市坐标
N = size(point, 1); %计算城市个数
D = zeros(N, N); %初始化距离的邻接矩阵
T0 = 1e30; %初始温度
Tend = 1e-10; %终止温度
q = 0.9; %降温速率
%计算迭代次数
syms Time
eqn = T0 * q ^ Time == Tend;
Time = ceil(double(solve(eqn, Time)));
%计算各城市之间的距离
for i = 1 : N
for j = i + 1 : N
D(i, j) = sqrt((point(i, 1) - point(j, 1)) ^ 2 + (point(i, 2) - point(j, 2)) ^ 2);
D(j, i) = D(i, j);
end
end
%记录各温度下的路径
path = zeros(Time, N);
%记录各温度下的总距离
distance = zeros(Time, 1);
%记录所有温度下的最短路径
min_path = zeros(1, N);
%记录所有温度下的最短距离
min_distance = inf;
%随机选取初始城市顺序
S1 = randperm(N);
%开始迭代
for i = 1 : Time
%计算当前温度下S1的总距离
dis1 = pathLength(D, N, S1);
%进行随机两个城市位置的变换
S2 = S1;
index = round(rand(1, 2) * (N - 1) + 1);
S2(index(1)) = S1(index(2));
S2(index(2)) = S1(index(1));
%计算变换后的S2的总距离
dis2 = pathLength(D, N, S2);
%对比S1,S2的距离判断要保留哪一个
dc = dis2 - dis1;
if dc < 0 || exp(-dc / T0) > rand
path(i, :) = S2;
distance(i, :) = dis2;
S1 = S2;
else
path(i, :) = S1;
distance(i, :) = dis1;
end
%记录最优路线与距离
if distance(i, :) < min_distance
min_path = path(i, :);
min_distance = distance(i, :);
end
%降温操作
T0 = T0 * q;
%%绘制图像
%取出最优路径经过的点位
tempx_plot = point(min_path, 1);
tempy_plot = point(min_path, 2);
%将最优路径经过的点位的行列数倒置,确保与后面要拼接的矩阵保持相同行数,进而进行列拼接
x_plot = [tempx_plot.', [point(min_path(1), 1)]];
y_plot = [tempy_plot.', [point(min_path(1), 2)]];
%绘制各城市点位与最短路径
plot(x_plot, y_plot, 'b--', x_plot, y_plot, 'r*' );
title(['第', num2str(i), '次迭代']);
pause(0.1);
end
2.计算总距离函数
%计算总距离函数
function dis = pathLength(D, N, S1)
%UNTITLED3 此处显示有关此函数的摘要
% 此处显示详细说明
dis = 0;
for i = 1 : N - 1
dis = dis + D(S1(i), S1(i + 1));
end
dis = dis + D(S1(N), S1(1));
end
三、运行结果





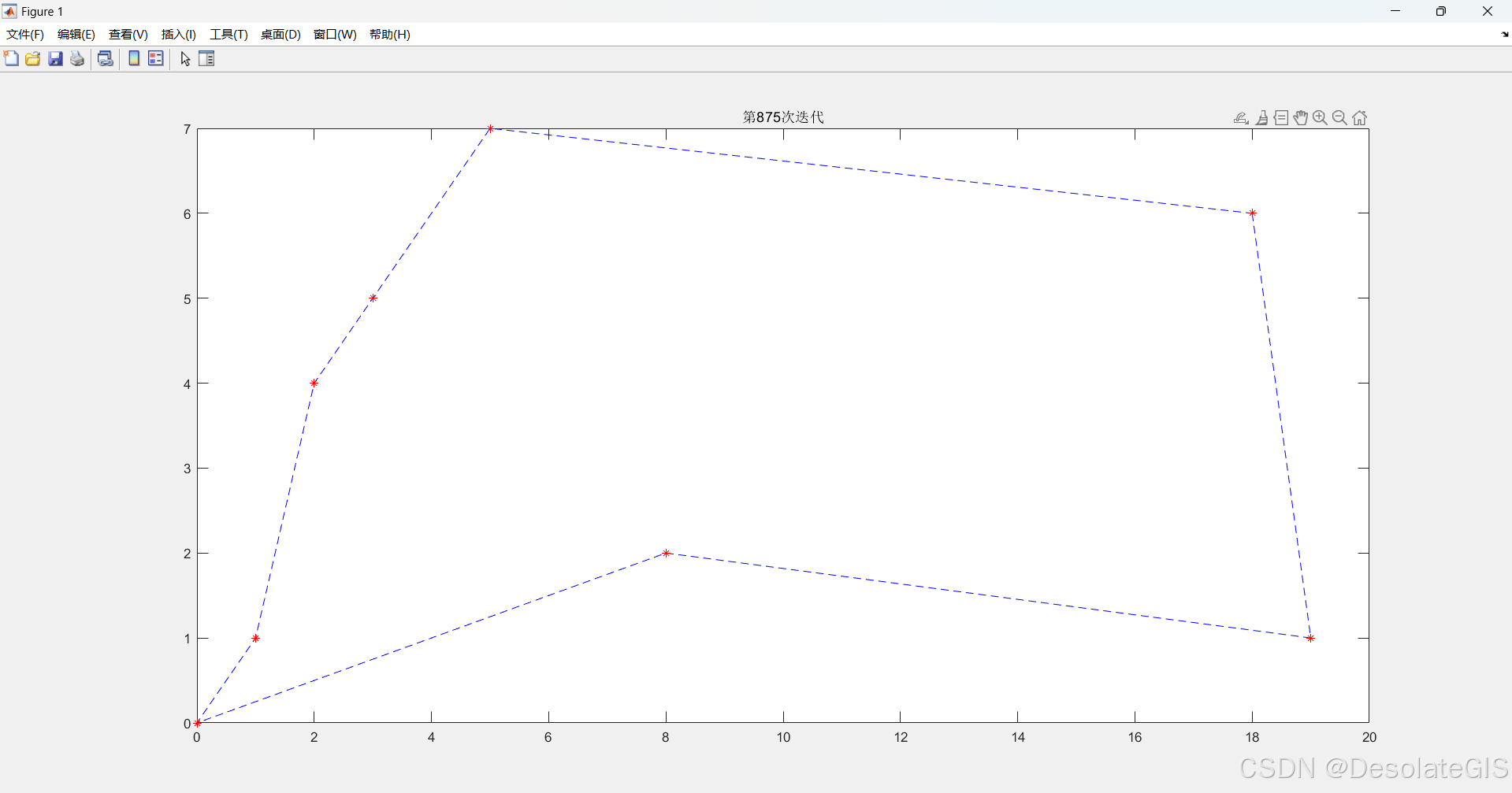
















 565
565

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








