数学建模：MATLB粒子群算法求函数最值

一、问题简述

给定一个函数表达式（二维或三维），求该函数的最值。

用粒子群算法解决此类问题。

 

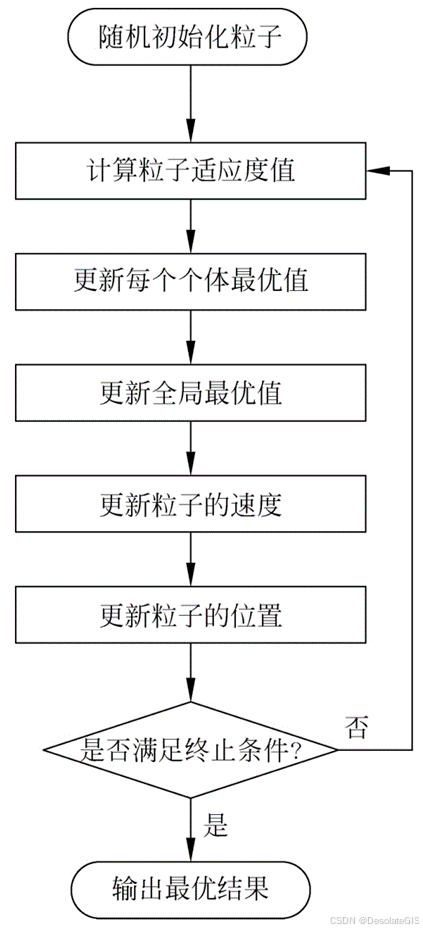
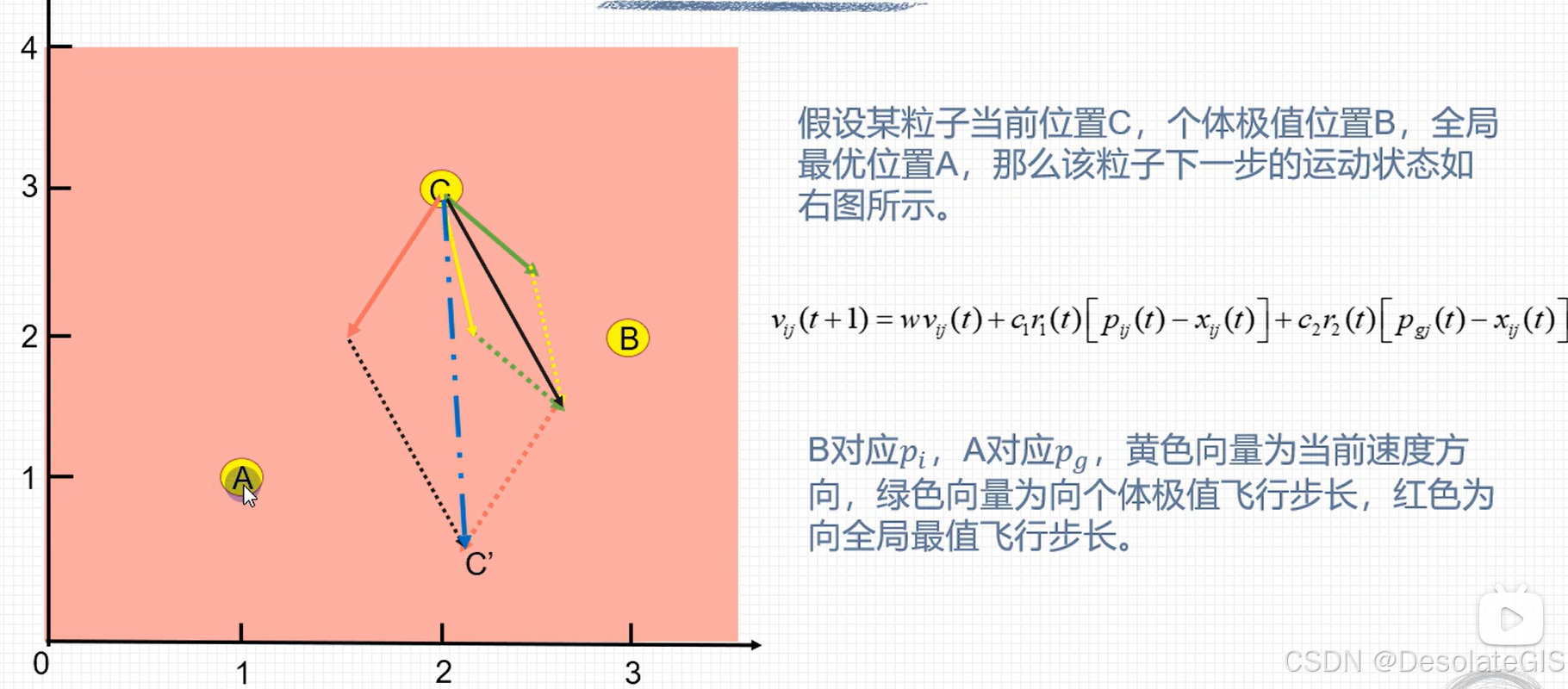
二、代码

clear
clc

f = @(x1, x2) 20 + x1.^2 + x2.^2 - 10*cos(2*pi.* x1) - 10*cos(2*pi.* x2);

%初始种群个数
N = 20;
%可行解维数
d = 2;
%迭代次数
G = 100;
%位置参数限制
limit = [-5.12, 5.12];
%每次移动距离参数限制
vlimit = [-0.5, 0.5];

%给二维的参数x1,x2按一定精度划分下标，用于绘制函数图像
x_plot1 = limit(1) : 0.05 : limit(2);
x_plot2 = limit(1) : 0.05 : limit(2);
%用meshgrid函数使得x_plot1, x_plot2不再是原本的一一对应组合，而是一个数组中的每个都与另一个数组中的所有项组合
[X1, X2] = meshgrid(x_plot1, x_plot2);
Y = f(X1, X2);

%惯性权重
w = 0.8;
%自我学习粒子
c1 = 0.5;
%群体学习粒子
c2 = 0.5;
%初始化第一代种群的位置和速度
per = limit(1) + rand(N, d) * (limit(2) - limit(1));
v = vlimit(1) + rand(N, 1) * (vlimit(2) - vlimit(1));

%历代个体函数值最小的位置
perMinX = zeros(N, d);
%历代种群函数值最小的位置
popMinX = zeros(1, d);

%当前种群的函数值最小的位置