[CQOI2015]选数，洛谷P3172，神奇的Dp或莫比乌斯反演+杜教筛

最新推荐文章于 2022-01-22 17:01:13 发布

Deep_Kevin

最新推荐文章于 2022-01-22 17:01:13 发布

阅读量297

点赞数

CC 4.0 BY-SA版权

分类专栏：莫比乌斯反演

本文链接：https://blog.youkuaiyun.com/Deep_Kevin/article/details/85164026

莫比乌斯反演专栏收录该内容

12 篇文章

订阅专栏

本文解析了一道数论与算法竞赛题，通过杜教筛、整除分块等技巧求解特定数学问题，同时介绍了另一种DP算法解法，详细展示了从公式推导到代码实现的过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

正题

题目链接给一下

题目已经很明显了，要我们求 $\sum_{i_1=L}^H...\sum_{i_n=L}^H[gcd(i_1,...,i_n)=K]$

还是变形一下， $\sum_{i_1=ceil(L/K)}^{floor(H/K)}...\sum_{i_n=ceil(L/K)}^{floor(H/K)}[gcd(i_1,...,i_n)=1]$

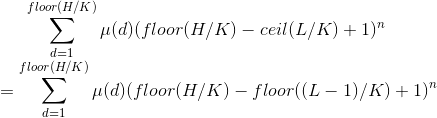
然后套路反演 $\sum_{d=1}^{floor(H/K)}\mu(d)(floor(H/K)-ceil(L/K)+1)^n \\=\sum_{d=1}^{floor(H/K)}\mu(d)(floor(H/K)-floor((L-1)/K)+1)^n$

因为H很大，所以前缀和用杜教筛求就好了，然后整除分块，大概时间复杂度就是非线性的吧。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<map>
#include<cmath>
using namespace std;

int n,k,l,r;
int mu[1000010],P[200010];
long long mus[1000010];
bool vis[1000010];
int maxn=1e6;
long long mod=1e9+7;
map<int , long long> sum;

long long get_mu(int x){
	if(x<=maxn) return mus[x];
	if(sum[x]) return sum[x];
	int L=2,R;
	long long ans=1;
	while(L<=x){
		R=x/(x/L);
		(ans-=(R-L+1)*get_mu(x/L))%=mod;
		(ans+=mod)%=mod;
		L=R+1;
	}
	return sum[x]=ans;
}

long long ksm(long long x,long long t){
	long long tot=1;
	while(t){
		if(t%2) (tot*=x)%=mod;
		(x*=x)%=mod;
		t/=2;
	}
	return tot;
}

long long get_ans(){
	int L=1,R;
	long long ans=0;
	while(L<=r){
		R=min(L<=l?l/(l/L):(int)1e9,r/(r/L));
		ans+=(get_mu(R)-get_mu(L-1))*ksm(r/L-l/L,n)%mod;
		(ans=ans%mod+mod)%=mod;
		L=R+1;
	}
	return ans;
}

int main(){
	scanf("%d %d %d %d",&n,&k,&l,&r);
	l=floor((double)(l-1)/k),r=floor((double)r/k);
	int temp=0;
	mu[1]=1;vis[1]=true;mus[0]=0;
	for(int i=1;i<=maxn;i++){
		if(!vis[i]) {P[++P[0]]=i;mu[i]=-1;}
		for(int j=1;j<=P[0] && (temp=i*P[j])<=maxn;j++){
			vis[temp]=true;
			if(i%P[j]==0) break;
			mu[temp]=-mu[i];
		}
		mus[i]=mus[i-1]+mu[i];
	}
	printf("%lld\n",get_ans());
}

点开题解，发现有一种很神的Dp做法。

首先，还是得到这条公式 $\sum_{i_1=ceil(L/K)}^{floor(H/K)}...\sum_{i_n=ceil(L/K)}^{floor(H/K)}[gcd(i_1,...,i_n)=1]$

我们怎么让他的gcd为1呢，或者说，我们怎么知道gcd为1的有多少对呢？

用 f(x) 记录x在 [ceil(L/K),floor(H/K)] 中是多少个组合的最大公约数。

暂且让 f(x)=d_x^n-d_x ，dx为x在这个区间内出现的次数，那么现在 f(x) 为不包括相同数字的组合，而且最大公约数为x的倍数的组合个数。

那么因为 x>H-L,f(x)=0 ，所以干脆不记录。

然后倒着做一次就可以了。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<cmath>
using namespace std;

int n,k,l,r;
long long mod=1e9+7;
long long f[1000010];

long long ksm(long long x,long long t){
	long long tot=1;
	while(t){
		if(t%2) (tot*=x)%=mod;
		(x*=x)%=mod;
		t/=2;
	}
	return tot;
}

int main(){
	scanf("%d %d %d %d",&n,&k,&l,&r);
	l=ceil((double)l/k),r=floor((double)r/k);
	int a,b;
	for(int i=1;i<=r-l;i++){
		a=ceil((double)l/i);b=floor((double)r/i);
		f[i]=(ksm(b-a+1,n)-(b-a+1)+mod)%mod;
	}
	if(l==1) f[1]++;
	for(int i=r-l;i>=1;i--){
		for(int j=2*i;j<=r-l;j+=i) f[i]-=f[j];
		(f[i]=f[i]%mod+mod)%=mod;
	}
	printf("%lld",f[1]);
}