正题
题目要求一个这样的东西: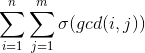 ,
,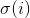 指的是i的约数和。
指的是i的约数和。
暂时不要求这个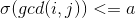
那么我们应该怎么变形。
首先,我们用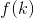 表示gcd(i,j)=k的有多少对,那么
表示gcd(i,j)=k的有多少对,那么
![f(k)=\sum_{i=1}^{floor(n/k)}\sum_{j=1}^{floor(m/k)}[gcd(i,j)=1]\\=\sum_{d=1}^{floor(n/k)}\mu(d)\frac{n}{kd}\frac{m}{kd}](https://i-blog.csdnimg.cn/blog_migrate/c351869c5f476626642c291bc9a0d285.png)
答案就变成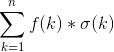
换进去,就变成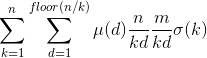
令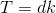 ,枚举T,得到:
,枚举T,得到:
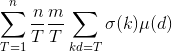
问题的关键,就变成了怎么快速求出后面这个sigma的前缀和,也就是说,我们令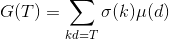
怎么求G的前缀和?
可以发现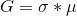 ,而这个
,而这个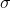 还受a的限制,
还受a的限制,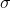 这个函数的某一位如果大于a,那么就为0,否则为原来的值。
这个函数的某一位如果大于a,那么就为0,否则为原来的值。
这样我们要对于每一组数据的每一组a,去构造一个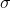 函数做一遍狄利克雷卷积???
函数做一遍狄利克雷卷积???
那就太慢了
考虑离线,将a排一遍序,然后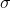 肯定只增不减,也就是说只会从没有变成有,对于这样的一次操作,我们先处理好每一个数的
肯定只增不减,也就是说只会从没有变成有,对于这样的一次操作,我们先处理好每一个数的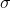 ,然后排一遍序,从小到大加入,然后做一次狄利克雷卷积总时间复杂度就是
,然后排一遍序,从小到大加入,然后做一次狄利克雷卷积总时间复杂度就是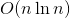 的。
的。
最后,G要求前缀和,改点求段直接套个树状数组就可以了!
总共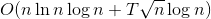
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lowbit(x) (x&(-x))
using namespace std;
int T;
const int maxn=1e5;
int sum[maxn+10];
int mu[maxn+10],p[maxn+10];
bool vis[maxn+10];
int ans[20010];
struct ques{
int n,m,a,id;
bool operator<(const ques q)const{
return a<q.a;
}
}s[20010];
struct node{
int x,d;
bool operator<(const node p)const{
return d<p.d;
}
}d[maxn+10];
void add(int x,int t){
while(x<=maxn){
sum[x]+=t;
x+=lowbit(x);
}
}
int get_sum(int x){
int tot=0;
while(x>=1){
tot+=sum[x];
x-=lowbit(x);
}
return tot;
}
int main(){
scanf("%d",&T);
for(int i=1;i<=T;i++) scanf("%d %d %d",&s[i].n,&s[i].m,&s[i].a),s[i].id=i;
sort(s+1,s+1+T);
for(int i=1;i<=maxn;i++) {
d[i].x=i;
for(int j=i;j<=maxn;j+=i) d[j].d+=i;
}
sort(d+1,d+1+maxn);
mu[1]=1;vis[1]=true;
int temp;
for(int i=1;i<=maxn;i++){
if(!vis[i]) {p[++p[0]]=i;mu[i]=-1;}
for(int j=1;j<=p[0] && (temp=i*p[j])<=maxn;j++){
vis[temp]=true;
if(i%p[j]==0) break;
mu[temp]=-mu[i];
}
}
int k=1,l,r,an;
for(int i=1;i<=T;i++){
while(k<=maxn && d[k].d<=s[i].a){
for(int j=1;j*d[k].x<=maxn;j++) if(mu[j]!=0) add(j*d[k].x,mu[j]*d[k].d);
k++;
}
l=1,r,an=0;
if(s[i].n>s[i].m) swap(s[i].n,s[i].m);
while(l<=s[i].n){
r=min(s[i].n/(s[i].n/l),s[i].m/(s[i].m/l));
an+=(s[i].n/l)*(s[i].m/l)*(get_sum(r)-get_sum(l-1));
l=r+1;
}
ans[s[i].id]=(an&2147483647);
}
for(int i=1;i<=T;i++) printf("%d\n",ans[i]);
}







 本文探讨了一种使用狄利克雷卷积优化算法的问题解决策略,通过离线处理和树状数组实现高效求解,关键在于快速计算特定数学函数的前缀和。
本文探讨了一种使用狄利克雷卷积优化算法的问题解决策略,通过离线处理和树状数组实现高效求解,关键在于快速计算特定数学函数的前缀和。
















 1396
1396

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








