[HAOI2006]数字序列，洛谷P2501，Dp+较大的思维深度+神定理

最新推荐文章于 2023-10-15 00:32:56 发布

原创最新推荐文章于 2023-10-15 00:32:56 发布 · 528 阅读

0 ·

CC 4.0 BY-SA版权

本文详细解析了一道算法竞赛题目，重点在于如何求解最长不下降子序列，并通过巧妙的优化策略解决后续复杂问题。采用O(nlog2n)高效算法，对序列进行预处理，再结合动态规划思想，最终得出最优解。

正题

题目链接在这里

好像很难，第一问都不知道怎么做。。。

假设我们已经知道第一问的答案序列 $Ans_i$ ，一个结论就是 $a_{Ans_i}-a_{Ans_j}>=Ans_i-Ans_j$ ，（因为如果连中间塞数都满足不了，那么就一定不是答案

变形： $a_{Ans_i}-Ans_i>=a_{Ans_j}-Ans_i$

我们令 $b_i=a_i-i$ ，那么对于答案序列，满足 $b_{Ans_i}>=b_{Ans_j}$

这就很明显是求b的最长不下降子序列，O(n log2 n)做法很明了。

第一问解决！

考虑一下第二问。

对于 $b_{Ans_i}$ 和 $b_{Ans_{i+1}}$ ，都满足 $b_k<b_{Ans_i} || b_k>b_{Ans_{i+1}}(k>\in (Ans_i,Ans_{i+1}))$ ，（因为如果在他们两个b值之间，那么就会被算进答案

我们先把这两个东西分成两部分，一部分是 $b_k<b_{Ans_i}$ 的，一部分是 $b_k>b_{Ans_{i+1}}$ 的。

先用最小的代价使它靠近 $b_{Ans_i}$ 或者 $b_{Ans_{i+1}}$ 。就像下图这样。

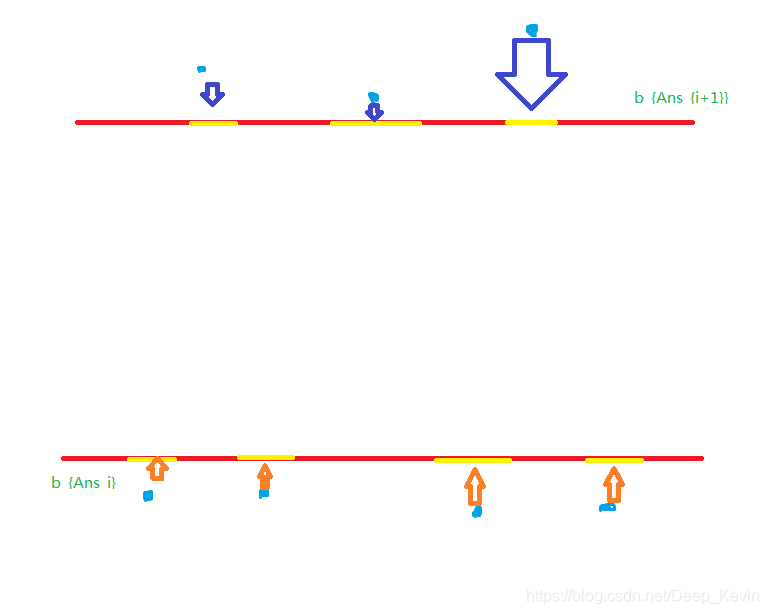
先把它们靠近两条线。

但是又发现现在b还是没有规律的，我们来试着让他变得有规律。

如果一条点不在左右相邻两点之间，我们就要比较靠左还是靠右更优一些。

经过不断的尝试和试验，可以得出一个点要么靠下面，要么靠上面，而且具有划分性。

也就是说，对于一个k，有 $\\b_k=b_{Ans_i}(k\in [Ans_i,k]) \\b_k=b_{Ans_{i+1}}(k\in [k+1,Ans_{i+1}])$ 。

神结论。

处理一个前缀和就好了。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int n;
int a[35010],b[35010];
int mmin[35010];
int f[35010];
long long g[35010];
struct edge{
	int y,next;
}s[35010];
int first[35010];
long long sum[35010];
long long last[35010];
int len=0;

void ins(int x,int y){
	len++;s[len].y=y;s[len].next=first[x];first[x]=len;
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]),b[i]=a[i]-i;
	memset(mmin,63,sizeof(mmin));
	mmin[0]=0;
	int l=0,r=0;b[n+1]=1e9;
	for(int i=1;i<=n+1;i++){
		int ll=l,rr=r;
		int ans=0;
		while(ll<=rr){
			int mid=(ll+rr)/2;
			if(mmin[mid]<=b[i]){
				ans=mid;
				ll=mid+1;
			}
			else rr=mid-1;
		}
		f[i]=++ans;
		if(ans>r) ++r;
		mmin[ans]=b[i];
		ins(f[i],i);
	}
	printf("%d\n",n+1-r);
	memset(g,20,sizeof(g));
	g[0]=0;
	b[0]=-1e9;
	ins(0,0);
	for(int x=1;x<=n+1;x++)
		for(int i=first[f[x]-1];i!=0;i=s[i].next){
			int y=s[i].y;
			if(y>x) continue;
			if(b[y]>b[x]) continue;
			sum[0]=0;
			for(int k=y+1;k<=x;k++)
				sum[k-y]=sum[k-y-1]+abs(b[k]-b[y]);
			last[x-y]=0;
			for(int k=x-1;k>=y;k--)
				last[k-y]=last[k-y+1]+abs(b[k]-b[x]);
			for(int k=y;k<x;k++)
				g[x]=min(g[x],g[y]+sum[k-y]+last[k+1-y]);
		}
	printf("%lld",g[n+1]);
}