官网的定义:

解释:在指定的维度下,对给定的数组进行从小到大排序,最后一个数组为主排序数组,其与数组为辅助排序数组,返回的是主排序数组的索引.
例子:
加上索引后的a:
加上索引后的b:
numpy.lexsort((b, a)) 函数的含义:
先对数组a按照从小到大的顺序进行排序, 对于数组a中相同的数字,无法进行排序比较.则去数组b中找相同索引所对应的值,并依据他们的大小来对a中相同索引对应的值进行排序,最后返回排好序之后的数组a的索引值.
对a进行初次排序后的值如下,其中3和5的索引能确定,但是1和4现在没法确定,因为当出现相同的数字时, lexsort的排序不是按照它原来的顺序来排序的.
此时,对于数组a中的1, 我们根据其索引值到数组b中去找相同索引值所对应的数字,然后根据他们的大小来确定a中相同数字的排序顺序. 如a中1的索引值为0和2, 我们在b中找索引值为0和2的数字是9和2. 因为2小于9,所以a中索引为2对应的数字排在索引为0对应的数字之前. 如此得到如下二次排序的结果:
依次,对于a中无法确定顺序的3个4. 注意他们在a中的索引值为:3,5,6. 我们在b中找相同索引所对应的数字.因为索引3对应的数字是4, 索引5对应的数字是2, 索引6对应的数字是1. 所以可以看到在b中, 索引6对应的数字<索引5对应的数字<索引3对应的数字. 相应的a中出现的顺序为:索引6对应的数字,索引5对应的数字,索引3对应的数字.于是,最终的排序如下:
代码验证:
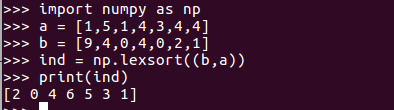
另一个比较复杂的例子:
numpy.lexsort((f, e, g))
对上面语句的分析: 先对e进行从小到大排序, f作为e的辅助排序.注意e的排序结果索引保持不变.然后对g进行从小到大的排序,e的排序结果作为g的辅助排序.
对e,f,g分别加上索引后的值如下:
按照上面的分析,先对e进行第一次从小到大的排序后成如下的结果. 其中3和3, 5和5排序索引暂时无法确定.
e中,数字 3 对应的索引为 0 和 5, 索引 0 和 5 在f中对应的数字为 8 和 8, 此时8和8无法进行比较排序,所以 e 中的 3 按出现的顺序排序. 即为:索引 0 对应的 3 在索引 5 对应的 3 之前.
同理,对于e中的两个5, 其对应的索引为 1 和 6.则在 f 中,相同的索引对应的数值为 9 和 1.所以,e中索引为 6 对应的 5 排在索引为 1 对应的 5 之前.
综上,e最终的排序如下:
接下来继续对 g 进行从小到大的排序, g的初次排序如下:
其中 4 和 4, 7和 7 的排序索引无法确定. 对于g中的 4 和 4, 其索引为 0 和 4, 在e中,相同的索引对应的数值为 3 和 8. 因为3<8, 所以在g中,索引 0 对应的 4 排在索引 4 对应的 4 之前.同理可得g中索引 5 对应的 7 排在索引 1 对应的 7 之前.
综上,g最终的排序如下:
numpy.lexsort((f, e, g)) 输出的内容为:[6 2 0 4 5 1 3]
代码验证:






 numpy.lexsort()函数用于在指定维度上对数组进行多重排序。它首先按最后一个数组进行排序,对于相同元素,使用前一个数组进行辅助排序,以此类推。文章通过实例详细解释了lexsort的工作机制,并提供了代码验证。
numpy.lexsort()函数用于在指定维度上对数组进行多重排序。它首先按最后一个数组进行排序,对于相同元素,使用前一个数组进行辅助排序,以此类推。文章通过实例详细解释了lexsort的工作机制,并提供了代码验证。

















 1526
1526

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








