摘要
在时间荧光显微镜图像序列中对颗粒的跟踪对量化细胞内结构以及病毒结构的动态过程至关重要。我们介绍了一种基于递归神经网络的概率深度学习方法,用于荧光颗粒(fluorescent particle)跟踪,该方法模拟了经典的贝叶斯滤波。与之前的颗粒跟踪深度学习方法相比,我们的方法考虑了不确定性,包括偶然性和认知不确定性。因此,可以确定计算轨迹的可靠性信息。无需手动调整跟踪参数,也不需要先验知识关于噪声统计。利用个体物体动态的短期和长期时间依赖性进行状态预测,并使用分配的检测结果更新预测状态。为了寻找对应关系,我们介绍了一个神经网络,该网络共同计算多个检测结果的分配概率,并确定漏检概率。训练仅需模拟数据,因此不需要繁琐的手动标注真实数据。我们基于合成和真实的二维以及三维荧光显微镜图像进行了定量性能评估。我们使用了颗粒跟踪挑战的图像数据以及显示病毒结构和染色质结构的实时荧光显微镜图像。结果表明,我们的方法提供了最先进的结果或改进了相对于先前方法的跟踪结果.
介绍
卷积神经网络(CNN)用于提取外观特征,生成辨别性外观模型,进行目标检测,计算分配分数,以及运动预测。递归神经网络(RNN)通常用于计算跟踪片段和检测(或跟踪片段和其他跟踪片段)之间的分配分数,这通常利用外观特征,而这些特征几乎无法用于跟踪不可区分的粒子。CNN和RNN被结合用于在模拟高能物理数据中找到检测器命中之间的对应,而不使用像贝叶斯滤波中的预测和更新步骤。
由于神经网络通常由大量参数和非线性激活组成,计算网络输出的(多模态(multi-modal))后验分布是不可处理的。因此,引入了近似方法(approximation methods),这些方法主要基于贝叶斯推断(Bayesian inference)或蒙特卡罗采样(Monte-Carlo sampling)。贝叶斯神经网络通过概率分布表示参数(权重),而不是使用单一值。因此,网络输出也可以通过概率分布表示,并通过图形模型(graphical models)或非线性信念网络(non-linear belief networks)进行解析计算。或者,也可以使用蒙特卡罗采样。通常,蒙特卡罗样本是通过神经网络的集成获得的。这些集成可以通过经过不同训练的神经网络生成或在训练和测试期间采用丢弃法(蒙特卡罗丢弃(Monte-Carlo dropout))来实现。然而,蒙特卡罗采样方法包括知识不确定性(模型不确定性),但不包括随机不确定性(数据不确定性)。
蒙特卡罗采样
基本原理:蒙特卡罗采样是一种基于随机抽样的数值计算方法。它通过从概率分布中抽取大量样本,利用这些样本来近似计算复杂的积分或概率分布等。在神经网络的上下文中,蒙特卡罗采样用于近似计算网络输出的后验分布。
在神经网络中的应用:
模型不确定性:通过在神经网络中引入随机性(例如,使用丢弃法),可以对模型的不确定性进行建模。例如,在蒙特卡罗丢弃中,每次前向传播时随机丢弃一部分神经元,从而生成多个不同的网络输出。这些输出的分布可以用来估计模型的不确定性。
集成方法:另一种常见的蒙特卡罗采样方法是训练多个不同的神经网络(集成),然后通过这些网络的输出来估计后验分布。每个网络可以有不同的初始化、训练数据子集或正则化方式,从而生成多样化的输出。
图形模型
基本概念:图形模型是一种用图来表示变量之间依赖关系的概率模型。它通过节点表示随机变量,边表示变量之间的条件依赖关系。图形模型可以分为有向图模型(如贝叶斯网络)和无向图模型(如马尔可夫随机场)。
在神经网络中的应用:
建模变量关系:在贝叶斯神经网络中,可以使用图形模型来表示神经网络参数(权重)之间的概率关系。例如,一个简单的贝叶斯网络可以将输入变量、隐藏层变量和输出变量之间的依赖关系以有向图的形式表示出来,通过这种方式可以更直观地理解网络的结构和变量之间的信息传递。
推断和计算:利用图形模型的结构,可以进行高效的概率推断。例如,通过变量消除算法或信念传播算法,可以在复杂的图形模型中计算出感兴趣的概率分布,如网络输出的后验分布。
非线性信念网络
基本定义:非线性信念网络是一种结合了非线性变换和信念传播的模型。它在传统的信念网络(如贝叶斯网络)的基础上,引入了非线性激活函数,使得网络能够处理复杂的非线性关系。这种网络可以看作是一种特殊的神经网络,其中每个节点的输出不仅取决于其输入变量,还受到非线性激活函数的影响。
在神经网络中的应用:
增强模型表达能力:通过引入非线性激活函数,非线性信念网络能够更好地捕捉数据中的复杂模式和非线性关系。例如,在图像识别任务中,非线性信念网络可以学习到图像特征之间的复杂非线性映射关系,从而提高模型的性能。
概率推断:类似于图形模型,非线性信念网络也可以进行概率推断。通过在非线性变换后的变量之间应用信念传播算法,可以计算出网络输出的概率分布。这种方法结合了神经网络的非线性拟合能力和图形模型的概率推断能力,适用于一些需要同时考虑非线性和概率不确定性的任务。
在本次贡献中,我们提出了一种新的深度神经网络架构,用于跟踪荧光显微镜图像中的粒子,该架构利用了随机不确定性和认知不确定性(aleatoric and epistemic uncertainty),我们验证了网络能够捕捉到这两种类型的不确定性。受到经典贝叶斯滤波的启发,网络学习预测下一个状态,并根据分配的检测来修正预测状态。使用门控递归单元(gated recurrent units(GRUs))来利用单个物体动态的短期和长期时间依赖性。通过变分贝叶斯学习引入认知不确定性,使用低限界的近似以实现高效学习,这不需要计算代价昂贵的迭代推理方案,如马尔可夫链蒙特卡洛(Markov chain Monte Carlo)。使用重参数化(reparameterization)的贝叶斯层,其中参数由高斯分布表示。在通过变分推理(variational inference)进行网络训练时,这些概率分布的参数会被学习,而不是直接学习网络权重。为了捕捉由于粒子探测器和物体运动噪声引起的随机不确定性,网络学习估计高斯分布的均值和标准差,从中可以确定预测和更新状态。我们还引入了一种神经网络,该网络根据预测状态与通过点增强滤波器(spot-enhancing filter(SEF))和高斯拟合(Gaussian fitting)获得的粒子检测之间的欧几里得距离(Euclidean distance),确定对应查找的分配概率(assignment probabilities)。分配概率是在多个检测中共同计算的,同时也确定了漏检的概率(missing detections)。网络训练仅使用合成数据,不需要手动标注的数据。
除了考虑和利用不确定性信息外,我们还提出了一种新颖的神经网络架构,该工作未使用贝叶斯滤波中的预测和更新步骤,也未使用贝叶斯层和GRU层。此外,我们这里使用了不同的损失函数,即平衡聚焦损失(balanced focal loss)以及不同的激活函数(PReLU)。我们基于合成和真实的二维以及三维荧光显微镜图像进行了定量性能评估。我们使用了粒子跟踪挑战赛的数据以及显示丙型肝炎病毒(HCV)蛋白NS5A、HCV相关蛋白ApoE和在DNA复制过程中标记的染色质结构的真实活细胞显微镜图像序列。结果表明,我们的方法相较于先前的方法达到了最先进或更好的结果。
方法
在本节中,我们介绍了一种新颖的概率深度学习方法,用于在活细胞荧光显微镜图像中跟踪多个粒子,称为深度概率粒子跟踪器(Deep Probabilistic Particle Tracker(DPPT))。
方法概述
对于粒子检测,我们采用点增强滤波器(SEF)和高斯拟合,产生一组由图像位置表示的检测。对于状态预测和状态更新,引入了一个具有门控循环单元(GRUs)的递归神经网络(RNN),模拟经典的贝叶斯滤波。这一网络考虑了随机性和认知不确定性。认知不确定性(epistemic uncertainty)通过学习网络参数的高斯分布来捕获。为了考虑随机性的不确定性(aleatoric uncertainty),网络估计高斯分布的均值和标准差,从中计算预测和更新的状态。为了寻找对应关系,我们引入了一个神经网络,该网络确定预测状态与粒子检测之间的分配概率以及缺失检测的概率。采用Jonker-Volgenant最短增广路径算法(Jonker-Volgenant shortest augmenting path algorithm)建立基于所有对象的计算分配概率(assignment probabilities)和缺失检测概率(probabilities of missing detections)的一一对应关系。
经典贝叶斯滤波(Bayesian filtering)框架
我们在时间点 t 的时间显微镜图像序列(temporal microscopy image sequence)中用状态向量(state vector) 表示生物粒子 i ,这通过噪声测量(noisy measurement)
来反映。在我们的设置中,粒子状态
和检测
都通过时间点 t 的图像位置来描述,因此 D 为实验设置中图像维度的数量。
状态向量(state vector):
如果生物粒子在二维平面上运动,状态向量可能包含 (x,y) 坐标;如果在三维空间中运动,则可能包含 (x,y,z) 坐标。
贝叶斯滤波的目标是根据一系列噪声检测 递归地估计
。对于每一个时间点 t,这个估计过程包含两个连续步骤:预测(prediction)和更新(update)。
- 预测:基于时间点 t - 1 的后验分布(1)
,预测步骤使用动态模型
来评估粒子动态,从而确定时间点 t 的先验分布
。
- 更新:通过应用贝叶斯定理,从先验分布
计算时刻 t 的后验分布
,并通过测量模型
结合检测
:(2)
状态 可以从后验分布
中确定。解决 (1) 和 (2) 的两种最常见的方法是卡尔曼滤波和粒子滤波。相反,我们提出了一种深度学习方法,以模仿经典的贝叶斯滤波。
用于预测和更新的贝叶斯神经网络
模仿经典贝叶斯滤波的深度学习架构
提议的概率神经网络模拟经典的贝叶斯滤波。网络架构可以细分为状态预测和更新模块。
- 预测模块使用基于GRU的RNN,利用个体粒子动态中的短期和长期时间依赖性来估计其下一个状态。
- 更新模块根据分配的检测来修正预测状态。
网络中使用贝叶斯层来考虑认知不确定性。此外,计算预测和更新状态的标准差,以提供关于随机不确定性的信息。对于每个时间点 t−1,网络为粒子 i 计算出两个输出向量以用于下一个时间点 t:预测状态 和更新状态
。
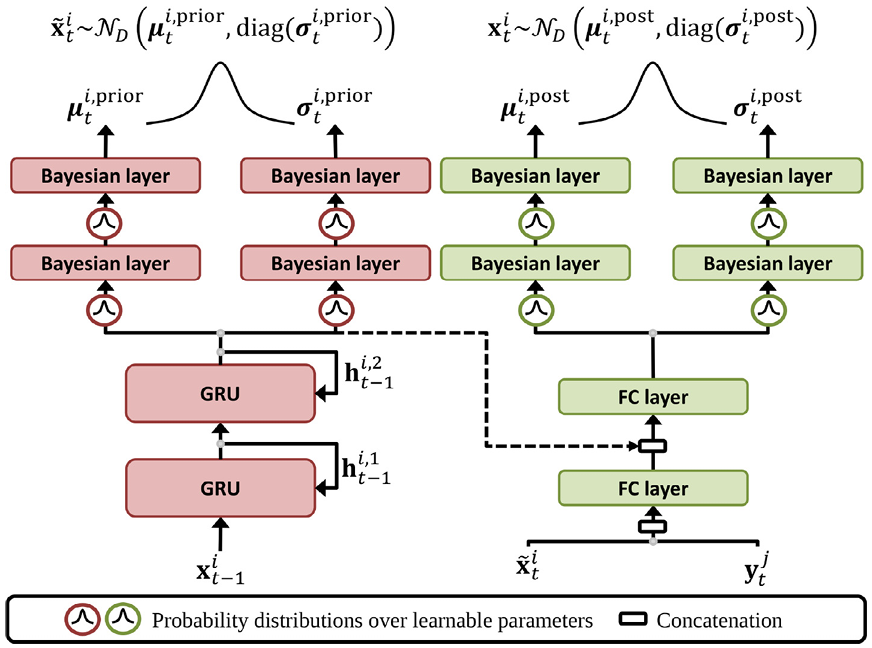
我们网络的预测模块由 L 个 GRU 层组成(我们使用 L = 2),每个层由 K 个单元组成。GRU 的结构能够捕捉短期和长期的时间依赖关系。为了解决标准 RNN 中出现的梯度消失和梯度爆炸问题,GRU 使用一个隐藏状态和两个门控来调节在每个时间点需要保留或丢弃的信息。这种门控设计类似于长短期记忆(LSTM)网络,然而,GRU 比 LSTM 更简单(例如,它只有两个门,而 LSTM 有三个门),计算速度更快。GRU 的重置门(reset gate)决定了前一个隐藏状态的哪个部分与当前输入结合以计算候选状态(candidate state)。GRU 的更新门(update gate)决定了保留前一个隐藏状态的哪个部分,以及从重置门得出的候选状态的哪个部分被添加到最终的隐藏状态中。更详细地说,时间点 t 上 l 层的隐藏状态表示为 ,而
表示网络输入向量。最后一个 GRU 层的输出表示为
。为了预测对象 i 在下一个时间点 t 的状态,使用时间点 t - 1 的对象状态向量
作为输入向量,即
。对于特定的 GRU 层 l 和时间点 t,更新门(3)
和重置门(4)
是根据时间点 t - 1 的前一个隐藏状态
和前一个 GRU 层的隐藏状态
计算的。其中
、
、
、
、
和
代表两个门的可学习参数。σ 是逻辑 sigmoid 激活函数。
那么,新候选状态(5)![]() 就可以计算。其中
就可以计算。其中 、
和
是可学习的参数。
表示逐元素(哈达玛乘法(Hadamard))乘法,而 tanh 是双曲正切激活函数。前一隐藏状态
和候选状态
由更新门
加权,以确定新的隐藏状态(6)
![]()
哈达玛乘法(Hadamard product),也称为元素乘法(element-wise product)或逐点乘法(pointwise product),是两个矩阵或向量的对应元素相乘得到的新矩阵或向量。
最后,最后一层GRU的隐藏状态被输入到两个独立的头部,每个头部由两个连续的贝叶斯层组成,分别使用K和D参数化的修正线性单元(Parametric Rectified Linear Units(PReLU))。我们使用PReLU,因为该激活函数包含一个可学习的参数(负输入值的斜率参数),以克服死亡ReLU问题(对任何输入值输出零的非活动ReLU)以及LeakyReLU对负输入值不一致预测的问题。两个头部的输出向量表示先验概率分布的均值
和标准差
,该分布被建模为高斯分布
。从这个先验分布中获得预测状态(7)
![]() 。因此,预测状态仅依赖于对象的当前状态
。因此,预测状态仅依赖于对象的当前状态 和 GRU 层的隐藏状态
。
“独立的头部”(independent heads):
通常指的是网络结构中并行的、相互独立的子网络部分,它们共享相同的输入,但各自进行不同的处理,并且通常用于不同的任务或目标。
“最后一层GRU的隐藏状态被输入到两个独立的头部。”意味着GRU的输出被分成两部分,每部分分别进入一个独立的子网络(头部)。每个头部由两个连续的贝叶斯层组成,这些贝叶斯层使用PReLU作为激活函数,并且分别用参数 K 和 D 进行参数化。
GRU的隐藏状态 ───┐ │ ├───> 头部1: 贝叶斯层1 (PReLU, 参数K) ──> 贝叶斯层2 (PReLU, 参数K) │ ├───> 头部2: 贝叶斯层1 (PReLU, 参数D) ──> 贝叶斯层2 (PReLU, 参数D)PReLU(Parametric ReLU):
一种改进的ReLU(Rectified Linear Unit)激活函数。ReLU是深度学习中广泛使用的激活函数,其定义为 f(x)=max(0,x)。虽然ReLU在许多任务中表现出色,但它有一个缺点:对于负输入,ReLU的输出始终为0,这可能导致部分神经元在训练过程中“死亡”,即这些神经元的梯度始终为0,无法更新参数。
为了解决这个问题,PReLU通过引入一个可学习的参数来处理负输入,从而避免了ReLU的“死亡神经元”问题。具体来说,PReLU的定义:
其中,α 是一个可学习的参数,通常是一个很小的正数。在训练过程中,α 会通过反向传播进行更新,从而使得网络能够更好地处理负输入。
随机和认知不确定性
考虑到为下一个时间点 t 分配的检测 ,状态被更新。首先,将向量
和
进行连接,并传递到一个具有 PReLU 的全连接层(FC layer),将其映射到维度为 K 的向量。然后,这个向量与最后一个 GRU 层的隐藏状态
进行连接, 致使一个维度为 2K 的向量传递到另一个具有 K 个 PReLU 的全连接层。最后,这个 K 维向量被输入到两个独立的头部中,每个头部由两个连续的贝叶斯层组成,分别为 K 和 D个PReLU。两个头的输出向量分别表示后验概率分布的均值
和标准差
,该分布建模为高斯分布
。从这个后验分布中获得更新的状态:(8)
![]() 。计算出的标准差
。计算出的标准差和
反映了数据中的噪声(例如,探测器噪声和运动噪声),并被称为随机不确定性。
为了考虑到不仅是随机不确定性,还有模型不确定性(即知识不确定性),我们在预测和更新模块的两个头部(总共四个网络头)中采用了贝叶斯层,其中可学习参数由概率分布(probability distributions)而不是单一值表示。由于精确的贝叶斯推断是不可处理的,我们采用变分近似(variational approximation)。通过对变分下界的重参数化,我们获得了一个可以使用标准随机梯度法直接优化的下界的可微估计器,这被称为证据下界(evidence lower bound(ELBO))。这种重参数化策略使得神经网络参数的高效学习成为可能,而不需要计算上昂贵的迭代推断方案。更具体地说,参数化为θ的变分后验分布Q(W;θ)用于可学习的参数W。变分后验分布Q(W;θ)的参数θ表示W的相关不确定性,通过变分推断学习得到。这是通过最大化证据下界目标来完成的:(9)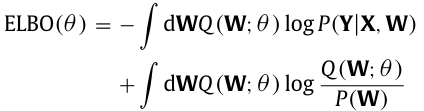
其中 P (W ) 是权重的先验分布,表示网络训练前权重的不确定性。贝叶斯层执行正则化(regularization),并施加约束,使后验分布 Q(W ;θ) 接近先验分布 P (W)。对于 Q(W ;θ) 和 P (W ),我们使用多元正态分布。P (Y | X , W ) 是似然函数,指定在网络输入 X 和可学习参数 W 下标签 Y 的变化。第二项(关于 P (W ) 的 Q(W ;θ) 的 Kullback-Leibler 散度)用于正则化并以解析方式确定,而第一项用于根据输入计算标签,并通过从 Q(W ;θ) 中抽取一组随机权重进行近似。计算第一项的采样产生了一组不同的网络输出。由于始终根据 Q(W ;θ) 采样新的权重集,因此每次应用四个网络头时,我们获得不同的先验分布 和后验分布
。
变分近似(Variational Approximation):
为了解决积分在高维空间中往往难以求解的问题,我们采用变分近似方法。变分近似通过引入一个简单的分布 Q(W;θ) 来近似真实的后验分布 P(W∣D)。这个分布 Q(W;θ) 被称为变分后验分布,其中 θ 是变分参数。
证据下界(ELBO):
变分下界:用于衡量 Q(W;θ) 与 P(W∣D) 的接近程度。它可以通过优化变分参数 θ 来最大化,从而使得 Q(W;θ) 尽可能接近 P(W∣D)。
重参数化技巧:为了使ELBO可微分,我们使用重参数化技巧。重参数化技巧允许我们将 Q(W;θ) 的采样过程表示为一个可微分的函数。这使得我们可以使用标准的随机梯度下降方法来优化ELBO,而不需要计算上昂贵的迭代推断方案。
正则化(regularization):
用于防止模型过拟合,提高模型的泛化能力。常见的正则化方法包括L1正则化、L2正则化、弹性网络正则化、Dropout和Early Stopping。通过在损失函数中添加正则化项,可以限制模型的复杂度,从而提高模型在新数据上的表现。
Kullback-Leibler 散度(Kullback-Leibler Divergence,简称 KL 散度):
一种衡量两个概率分布之间差异的非对称性度量。用于量化一个概率分布相对于另一个概率分布的“距离”。KL 散度越小,表示两个分布越相似。
因此,估计的先验和后验分布中的多样性反映了权重的不确定性(知识不确定性)。在我们的采样策略中,对于每个时间点t和粒子i,四个网络头被应用N次,产生N个先验和N个后验分布。我们选择N = 20,这是计算时间和跟踪性能之间的良好折中。从每一个先验和后验分布中分别获得一个预测状态和更新状态。最终的预测状态 和更新状态
分别通过对所有预测和更新状态进行平均来确定。
我们的概率网络的参数是通过最小化损失函数来学习的:(10)
其中是粒子i在时间点t的真实状态。损失函数由两个部分组成:用于状态预测(state prediction)和状态更新(state update)的负对数似然损失(negative log-likelihood loss)。损失函数表示与个体粒子i在时间点t对应的一个训练样本的损失。我们在所有实验中使用了λ= 1。对于训练,预测和更新模块被作为一个统一的网络使用。对于执行跟踪,这两个模块是顺序使用的。
计算对应查找的分配概率的神经网络架构
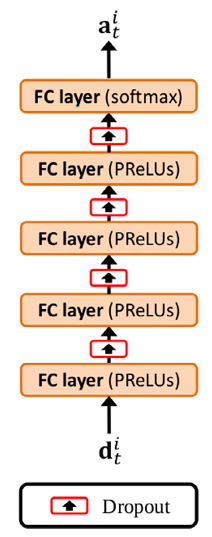
为了进行对应查找,我们提出了一种深度神经网络,该网络计算分配概率和缺失检测的概率。网络由四个连续的全连接层组成,每个层有 R 个 PReLU(我们使用 R = 512),最后是一个带有 softmax 归一化的全连接线性输出层。在每个全连接层(输出层除外)中,我们在训练过程中采用了 0.4 的 dropout 率以避免过拟合。
对于每个粒子 i 和时间点 t−1,网络以向量 为输入,其组件定义为
,表示粒子 i 在时间点 t 的预测状态与检测 j 之间的欧几里得距离。M 是在预测粒子 i 在时间点 t 的位置周围的半径为
的门内的检测数量(我们使用
= 20 像素)。由于门内的检测数量有所变化,并且我们的网络需要固定的输入大小,因此我们最多考虑门内的 M 个最近的检测(我们使用 M = 4)。如果门内的检测少于 M 个,我们用占位符(我们使用'−1')填充向量
。网络的最终输出向量
包含时间点 t 的归一化分配概率,即
,其中
表示丢失检测的概率,
表示粒子 i 与检测 j 之间的分配概率(对于 j = 1, ..., M)。计算的概率适应于局部邻域,例如,在物体密度较高的区域,缺失检测的概率较低。我们使用Jonker-Volgenant最短增广路径算法(Jonker-Volgenant shortest augmenting path algorithm),利用计算得出的分配概率和缺失检测的概率作为输入,以建立所有跟踪粒子与时间点t获得的检测集之间的一对一对应关系。由于网络计算概率,因此不需要阈值来判断缺失检测。
为了测量计算的分配概率 和真实值
之间的偏差,我们使用多类别变体的 α 平衡聚焦损失(multi-class variant of the α-balanced focal loss)。对于一个训练样本(个体粒子 i 的一个时间点 t),损失(11)
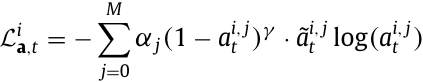 。其中 γ 是一个聚焦参数(focusing parameter),用于降低容易样本的权重并强调困难样本。在我们所有的实验中我们使用了 γ = 2。α∈ R M 1 代表权重因子,以应对训练数据中的类别不平衡,并根据训练数据中的类别分布进行计算。
。其中 γ 是一个聚焦参数(focusing parameter),用于降低容易样本的权重并强调困难样本。在我们所有的实验中我们使用了 γ = 2。α∈ R M 1 代表权重因子,以应对训练数据中的类别不平衡,并根据训练数据中的类别分布进行计算。
容易样本(Easy Samples):
容易样本是指模型能够轻松正确分类或预测的样本。这些样本通常具有以下特点:
特征明显:样本的特征与目标类别之间有很强的相关性,模型能够很容易地识别出这些特征。
分布集中:这些样本在特征空间中通常聚集在一起,与目标类别形成明显的簇。
预测置信度高:模型对这些样本的预测置信度很高,即模型输出的预测概率接近1(对于分类任务)或预测值与真实值非常接近(对于回归任务)。
困难样本(Hard Samples):
困难样本是指模型难以正确分类或预测的样本。这些样本通常具有以下特点:
特征模糊:样本的特征与目标类别之间的关系不明显,模型难以识别出这些特征。
分布分散:这些样本在特征空间中分布较为分散,与目标类别之间没有明显的边界。
预测置信度低:模型对这些样本的预测置信度较低,即模型输出的预测概率接近0.5(对于分类任务)或预测值与真实值差异较大(对于回归任务)。
噪声或异常值:这些样本可能包含噪声或异常值,使得模型难以正确处理。
网络训练
训练神经网络通常需要大量数据以实现收敛而不发生过拟合。由于真实荧光显微镜图像中粒子的真实数据几乎不可获得,且准确的手动标注非常繁琐,因此我们的DPPT网络仅使用模拟数据进行训练。在我们的数据模拟器中,粒子轨迹是基于不同运动模型进行模拟的,图像数据采用泊松噪声模型(Poisson noise model)生成,并从真实图像中自动提取信息。对于粒子动态,我们使用了四种不同的运动类型,即定向运动、布朗运动、定向运动与布朗运动之间的随机切换,以及加速运动。个别粒子的运动模型参数(例如扩散系数、速度、加速度)是从均匀分布中抽取的。对于扩散系数,我们在[1, 6]的区间内使用均匀分布,适用于粒子追踪挑战数据和活细胞荧光显微镜图像。对于速度,我们使用了[1, 6](定向运动)和[1, 4](加速运动和切换运动)的区间,对于加速度我们采用了[0.2, 0.8]。我们使用相对较大的间隔来增加网络的泛化能力。初始粒子位置和粒子的出现与消失都是由随机过程控制的。我们还模拟了移动出视野和失焦的情况。图像噪声由信噪比 反映,其中
是粒子的最大强度,
表示背景强度。与我们之前的工作不同,我们使用从真实图像中自动提取的信息来生成能够很好代表真实数据的训练图像。在我们的方案中,我们通过点增强滤波器检测真实图像中的粒子,并根据检测到的位置和局部邻域信息自动确定信噪比、粒子大小和粒子密度。我们在检测到的位置使用高斯拟合来确定
和
,以计算信噪比并确定粒子大小 σ。对于
、
和 σ,我们计算了所有检测到的粒子的均值和标准差。训练数据的信噪比根据真实数据中确定的信噪比进行设置。训练数据中个别粒子的外观参数(appearance parameters)
是从高斯分布中抽样的,其均值和标准差是在真实数据中确定的。训练数据中的粒子密度是根据真实图像中每帧确定的平均粒子检测数量设置的。相比之下,在我们之前的工作中,这些参数是从固定的手动定义区间的均匀分布中抽取的。图像大小、堆栈大小和位深度是根据真实数据的元信息设置的。与粒子追踪挑战模拟器(Particle Tracking Challenge simulator)相比,我们的模拟器的主要区别在于它包括了失焦运动和加速运动,并利用从真实图像中自动提取的信息生成能够很好代表真实数据的训练图像。
此外,我们利用网络计算的不确定性来选择生成的训练数据集,以便选择最适合的运动模型,从而使训练数据很好地代表真实图像。这是通过使用不同的运动模型训练我们的网络,并使用具有最低知识不确定性的跟踪结果来实现的。因此,我们利用了一个事实,即当训练数据中的粒子运动与真实数据中的运动很好地一致时,网络的知识不确定性较低。这种自动运动模型选择策略是新颖的,之前的工作中没有使用过。
此外,为生成训练数据,我们使用合成生成图像中的自动检测,以使网络能够学习检测器的错误。粒子检测采用了点增强滤波器(SEF)和高斯拟合。然后,生成的检测结果通过使用最近邻搜索(nearest neighbor search)和5像素的验证门映射到真实轨迹上。用于网络训练的轨迹和映射在其上的检测结果。因此,我们的方法不需要关于检测错误的先验知识,而是通过图像数据学习这些信息。这种训练策略允许生成能够很好代表真实数据的合成训练数据。
为了进行网络训练,我们使用了 AMSGrad 优化器,其中 β1 = 0.9 和 β2 = 0.999。我们使用的迷你批量(mini-batch size)大小为 64,贝叶斯神经网络的初始学习率为 = 0.02,而计算分配概率的网络的初始学习率为
= 0.001。为了避免过拟合,在收敛后进行早期停止。我们使用约 102,400 个来自合成图像序列的训练样本进行训练和验证。一个训练样本包括一个个体粒子的一个时间点。我们将数据集分为 80% 用于训练和 20% 用于验证。图像尺寸被标准化到范围 [0, 1]。我们的模型在使用 Tensorflow 2.1.0和 TensorFlow Probability 0.9.0的 Python 3.7 中实现。我们使用的计算机为配备 Intel(R) Core(TM) i7-7700HQ CPU、NVIDIA GeForce GTX 1050 Ti GPU 和 Linux 操作系统的笔记本电脑。
结论
我们提出了一种新颖的概率深度学习方法,用于跟踪荧光显微镜图像序列中的多个粒子。所提出的深度概率粒子跟踪器(DPPT)基于递归神经网络,模拟经典的贝叶斯滤波。与先前的粒子跟踪方法相比,我们的方法考虑了不确定性,包括内在的不确定性(数据中的固有噪声)和知识性不确定性(网络权重的不确定性)。该网络利用对象动态中的短期和长期时间依赖关系,预测下一个时刻的状态,并使用分配的检测来更新预测状态。为了寻找对应关系,我们引入了一种神经网络,能够在多个检测之间共同计算分配概率,并确定缺失检测的概率。网络训练只需模拟数据,因此不需要繁琐的手动标注真实值。我们提出了一种新颖的方案,利用从真实图像自动提取的信息生成合成训练数据。这使得能够模拟大量能够很好代表应用中图像的训练数据。
我们验证了提出的贝叶斯神经网络能够捕获两种类型的不确定性(随机性不确定性和认知不确定性),并进行了不确定性估计的评估。我们网络的一个优势在于可以确定提取轨迹的可靠性信息。我们证明计算出的不确定性可以被利用,以通过排除不可靠的跟踪点来提高后续运动分析的准确性。此外,我们还展示了不确定性可以被用来评估训练数据的适用性,并选择具有最佳运动模型的训练数据集,从而使训练数据更好地代表应用中的真实数据。不确定性还可以用于通过调整采集参数来校准显微镜实验。我们使用粒子跟踪挑战的二维和三维图像数据以及二维和三维实时活细胞荧光显微镜图像序列,对跟踪性能进行了定量评估。与之前的方法比较显示,DPPT取得了最先进或更好的结果。在未来的工作中,我们将把DPPT应用于其他应用的荧光显微镜图像。
参考文献:
Deep probabilistic tracking of particles in fluorescence microscopy images (2021)





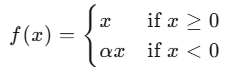
















 2599
2599

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








