【AI x FPGA自学笔记】基于参数化FPGA的通用在线神经网络的开发与实现

通过利用FPGA的可重构性，将基于参数化软件的人工神经网络（ANN）和ANN模拟器的灵活性转移到硬件平台上。这样做，我们将使用户能够在硬件上高效地探索设计空间和原型，正如现在在软件中所能做到的那样。

先前研究：羊群抗虫线虫检测的人工神经网络FPGA实现

MLP的构建

由于多层感知器神经网络（multi layer perceptron neural network（MLP））在数据分类和数据估计方面具有很高的效率，我们使用MLP来构建网络。

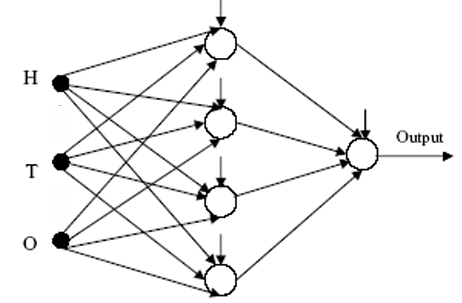
为了制作表1中的人工神经网络数据，使用一些羊群的兽医数据作为神经网络的输入和输出。这些统计数据的目的是建立一个多层感知网络（图1），用于模式识别和数据分类。MLP将用于苯并咪唑（BZD）耐药线虫的鉴定。

表1：显示了在药物注射前后受测畜群中
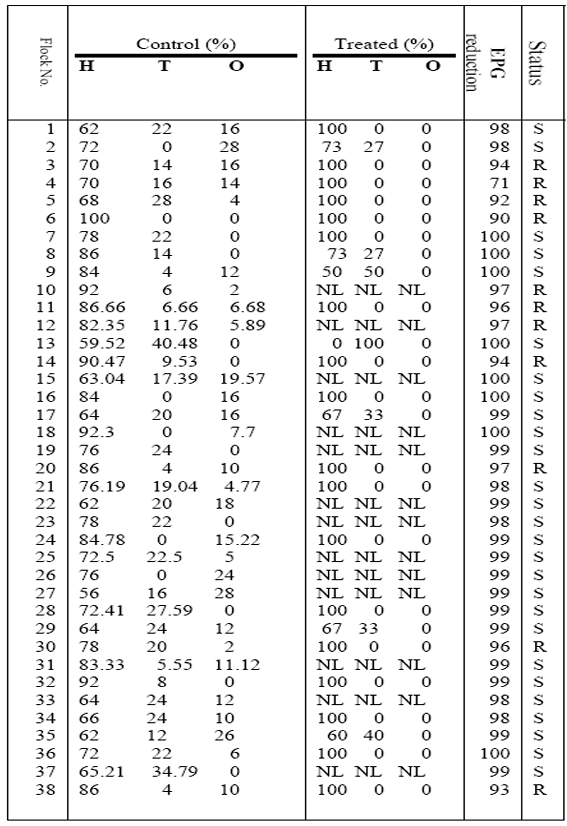
H、T、O寄生虫存在的百分比

图1：绵羊BZD耐药线虫多层感知器的构建

对于神经网络的训练，采用一种简单的反向传播方法来达到期望的最小误差。然后将训练得到的权重和偏置因子（bias factors）用于FPGA上的硬件安装。

所有在表1中给出的38行有三个输入和一个用于训练网络的输出。这38行中，前34行数据作为训练数据，后4行作为验证数据。

采用了一个具有一个隐藏层的网络来构建一个用于识别抗苯并噻二唑类杀虫剂的线虫的结构。该网络在输入层有 3 个节点（图 1），这些节点代表在对照组中临床发现的感染性幼虫（H、T 和 O）所占的百分比——这些幼虫无需对动物进行任何治疗。在网络的输出层有一个节点，其目标值被设定为 0 以对应对苯二氮䓬类药物有抗药性的线虫，而为对应易感线虫则设定为 1。网络的隐藏层有 4 个神经元，并使用了 Sigmoid 激活函数。为了训练该网络，从表 1 中选取了 1 到 34号群的数据作为训练数据，并采用反向传播学习规则来调整网络的权重。大约 300 个周期后，学习误差已经大大下降。

通过MATLAB训练得到的权重和偏倚系数如下：

W= [ 20.8274, -25.3639 , -4.8864;

        30.6564, -118.1918, -65.5309;

        43.8998, -60.2949, 145.4259;

        106.9770, -15.0551, -20.7781];

U= [117.1778;

      142.0364;

      106.8569;

      82.6105];

这些权重和偏倚系数将在后续步骤中用于训练和设计的网络的硬件安装。在获得权重和偏差系数后，将表 1 的最后 4 行应用于网络，以验证网络的正常运行情况。

ANN的FPGA实现

我们以上一节中所介绍的网络为例，在FPGA上进行实现。

图3：在FPGA上实现网络，XLINK系列XC400

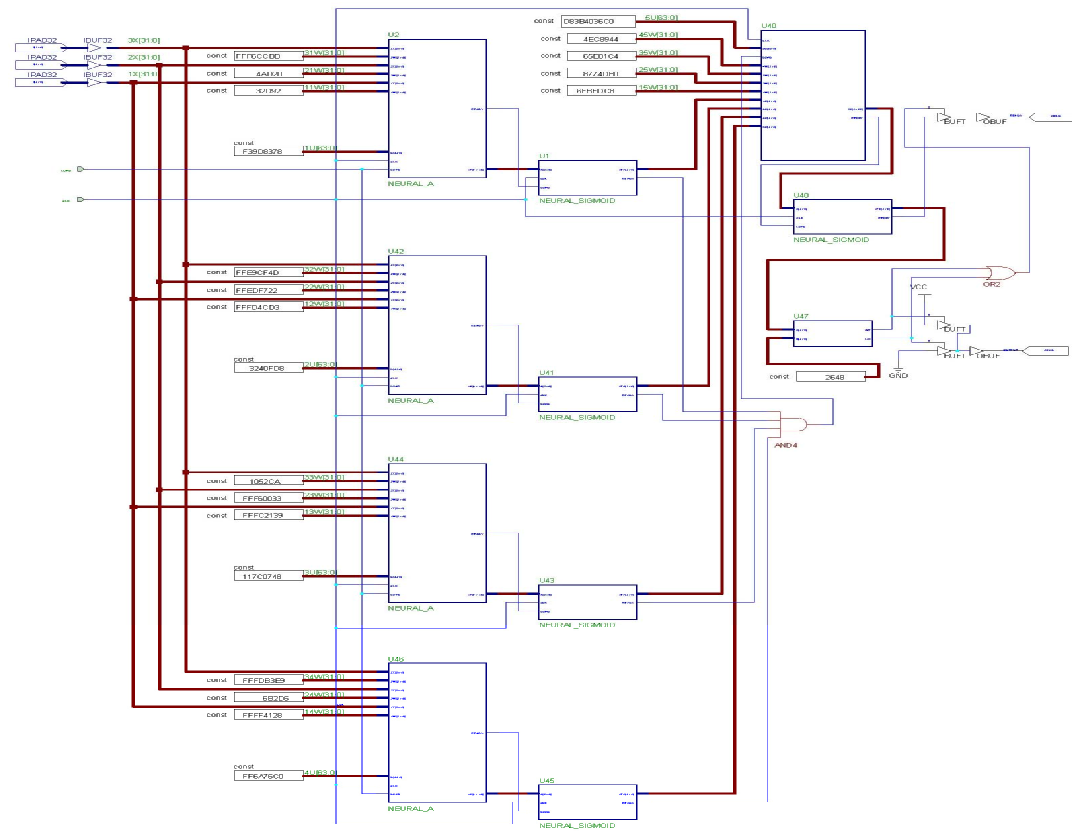
该网络在隐藏层有4个神经元，在输出层有1个神经元，每个隐藏层神经元有3个输入、3个权重因子和1个偏置因子。这些因子经过MATLAB仿真得到，现在可以认为是神经元的恒定输入。每一个