【OpenCV】 3D-2D:PnP算法原理(PnP的几种方法总结)
【OpenCV】 n 点透视问题数学建模及其求解(P3P方法)
1. 算法小结
enum SolvePnPMethod {
SOLVEPNP_ITERATIVE = 0,
SOLVEPNP_EPNP = 1, //!< EPnP: Efficient Perspective-n-Point Camera Pose Estimation @cite lepetit2009epnp
SOLVEPNP_P3P = 2, //!< Complete Solution Classification for the Perspective-Three-Point Problem @cite gao2003complete
SOLVEPNP_DLS = 3, //!< A Direct Least-Squares (DLS) Method for PnP @cite hesch2011direct
SOLVEPNP_UPNP = 4, //!< Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation @cite penate2013exhaustive
SOLVEPNP_AP3P = 5, //!< An Efficient Algebraic Solution to the Perspective-Three-Point Problem @cite Ke17
SOLVEPNP_IPPE = 6, //!< Infinitesimal Plane-Based Pose Estimation @cite Collins14 \n
//!< Object points must be coplanar.
SOLVEPNP_IPPE_SQUARE = 7, //!< Infinitesimal Plane-Based Pose Estimation @cite Collins14 \n
//!< This is a special case suitable for marker pose estimation.\n
//!< 4 coplanar object points must be defined in the following order:
//!< - point 0: [-squareLength / 2, squareLength / 2, 0]
//!< - point 1: [ squareLength / 2, squareLength / 2, 0]
//!< - point 2: [ squareLength / 2, -squareLength / 2, 0]
//!< - point 3: [-squareLength / 2, -squareLength / 2, 0]
};

2. 算法测试
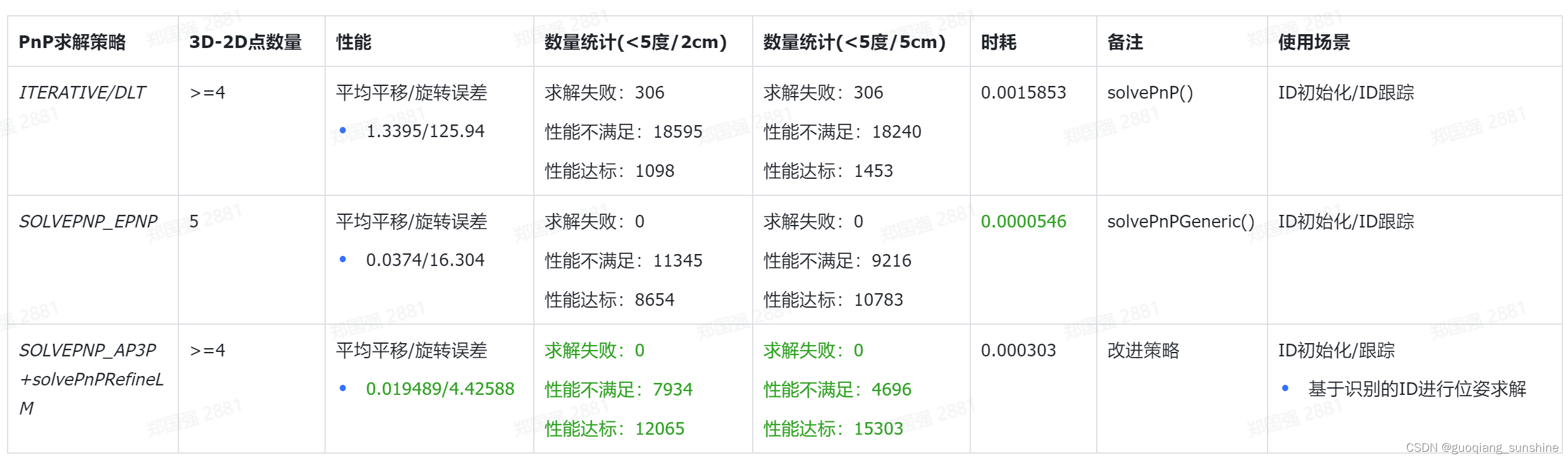
3. 算法解析
/** @brief Finds an object pose from 3D-2D point correspondences.
This function returns a list of all the possible solutions (a solution is a <rotation vector, translation vector>
couple), depending on the number of input points and the chosen method:
- P3P methods (@ref SOLVEPNP_P3P, @ref SOLVEPNP_AP3P): 3 or 4 input points. Number of returned solutions can be between 0 and 4 with 3 input points.
- @ref SOLVEPNP_IPPE Input points must be >= 4 and object points must be coplanar. Returns 2 solutions.
- @ref SOLVEPNP_IPPE_SQUARE Special case suitable for marker pose estimation.
Number of input points must be 4 and 2 solutions are returned. Object points must be defined in the following order:
- point 0: [-squareLength / 2, squareLength / 2, 0]
- point 1: [ squareLength / 2, squareLength / 2, 0]
- point 2: [ squareLength / 2, -squareLength / 2, 0]
- point 3: [-squareLength / 2, -squareLength / 2, 0]
- for all the other flags, number of input points must be >= 4 and object points can be in any configuration.
Only 1 solution is returned.
@param objectPoints Array of object points in the object coordinate space, Nx3 1-channel or
1xN/Nx1 3-channel, where N is the number of points. vector\<Point3d\> can be also passed here.
@param imagePoints Array of corresponding image points, Nx2 1-channel or 1xN/Nx1 2-channel,
where N is the number of points. vector\<Point2d\> can be also passed here.
@param cameraMatrix Input camera matrix \f$A = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\f$ .
@param distCoeffs Input vector of distortion coefficients
\f$(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6 [, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\f$ of
4, 5, 8, 12 or 14 elements. If the vector is NULL/empty, the zero distortion coefficients are
assumed.
@param rvecs Vector of output rotation vectors (see @ref Rodrigues ) that, together with tvecs, brings points from
the model coordinate system to the camera coordinate system.
@param tvecs Vector of output translation vectors.
@param useExtrinsicGuess Parameter used for #SOLVEPNP_ITERATIVE. If true (1), the function uses
the provided rvec and tvec values as initial approximations of the rotation and translation
vectors, respectively, and further optimizes them.
@param flags Method for solving a PnP problem:
- **SOLVEPNP_ITERATIVE** Iterative method is based on a Levenberg-Marquardt optimization. In
this case the function finds such a pose that minimizes reprojection error, that is the sum
of squared distances between the observed projections imagePoints and the projected (using
projectPoints ) objectPoints .
- **SOLVEPNP_P3P** Method is based on the paper of X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang
"Complete Solution Classification for the Perspective-Three-Point Problem" (@cite gao2003complete).
In this case the function requires exactly four object and image points.
- **SOLVEPNP_AP3P** Method is based on the paper of T. Ke, S. Roumeliotis
"An Efficient Algebraic Solution to the Perspective-Three-Point Problem" (@cite Ke17).
In this case the function requires exactly four object and image points.
- **SOLVEPNP_EPNP** Method has been introduced by F.Moreno-Noguer, V.Lepetit and P.Fua in the
paper "EPnP: Efficient Perspective-n-Point Camera Pose Estimation" (@cite lepetit2009epnp).
- **SOLVEPNP_DLS** Method is based on the paper of Joel A. Hesch and Stergios I. Roumeliotis.
"A Direct Least-Squares (DLS) Method for PnP" (@cite hesch2011direct).
- **SOLVEPNP_UPNP** Method is based on the paper of A.Penate-Sanchez, J.Andrade-Cetto,
F.Moreno-Noguer. "Exhaustive Linearization for Robust Camera Pose and Focal Length
Estimation" (@cite penate2013exhaustive). In this case the function also estimates the parameters \f$f_x\f$ and \f$f_y\f$
assuming that both have the same value. Then the cameraMatrix is updated with the estimated
focal length.
- **SOLVEPNP_IPPE** Method is based on the paper of T. Collins and A. Bartoli.
"Infinitesimal Plane-Based Pose Estimation" (@cite Collins14). This method requires coplanar object points.
- **SOLVEPNP_IPPE_SQUARE** Method is based on the paper of Toby Collins and Adrien Bartoli.
"Infinitesimal Plane-Based Pose Estimation" (@cite Collins14). This method is suitable for marker pose estimation.
It requires 4 coplanar object points defined in the following order:
- point 0: [-squareLength / 2, squareLength / 2, 0]
- point 1: [ squareLength / 2, squareLength / 2, 0]
- point 2: [ squareLength / 2, -squareLength / 2, 0]
- point 3: [-squareLength / 2, -squareLength / 2, 0]
@param rvec Rotation vector used to initialize an iterative PnP refinement algorithm, when flag is SOLVEPNP_ITERATIVE
and useExtrinsicGuess is set to true.
@param tvec Translation vector used to initialize an iterative PnP refinement algorithm, when flag is SOLVEPNP_ITERATIVE
and useExtrinsicGuess is set to true.
@param reprojectionError Optional vector of reprojection error, that is the RMS error
(\f$ \text{RMSE} = \sqrt{\frac{\sum_{i}^{N} \left ( \hat{y_i} - y_i \right )^2}{N}} \f$) between the input image points
and the 3D object points projected with the estimated pose.
The function estimates the object pose given a set of object points, their corresponding image
projections, as well as the camera matrix and the distortion coefficients, see the figure below
(more precisely, the X-axis of the camera frame is pointing to the right, the Y-axis downward
and the Z-axis forward).
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NtgL5SBe-1676463931479)(pnp.jpg)]
Points expressed in the world frame \f$ \bf{X}_w \f$ are projected into the image plane \f$ \left[ u, v \right] \f$
using the perspective projection model \f$ \Pi \f$ and the camera intrinsic parameters matrix \f$ \bf{A} \f$:
\f[
\begin{align*}
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix} &=
\bf{A} \hspace{0.1em} \Pi \hspace{0.2em} ^{c}\bf{T}_w
\begin{bmatrix}
X_{w} \\
Y_{w} \\
Z_{w} \\
1
\end{bmatrix} \\
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix} &=
\begin{bmatrix}
f_x & 0 & c_x \\
0 & f_y & c_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_x \\
r_{21} & r_{22} & r_{23} & t_y \\
r_{31} & r_{32} & r_{33} & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_{w} \\
Y_{w} \\
Z_{w} \\
1
\end{bmatrix}
\end{align*}
\f]
The estimated pose is thus the rotation (`rvec`) and the translation (`tvec`) vectors that allow transforming
a 3D point expressed in the world frame into the camera frame:
\f[
\begin{align*}
\begin{bmatrix}
X_c \\
Y_c \\
Z_c \\
1
\end{bmatrix} &=
\hspace{0.2em} ^{c}\bf{T}_w
\begin{bmatrix}
X_{w} \\
Y_{w} \\
Z_{w} \\
1
\end{bmatrix} \\
\begin{bmatrix}
X_c \\
Y_c \\
Z_c \\
1
\end{bmatrix} &=
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_x \\
r_{21} & r_{22} & r_{23} & t_y \\
r_{31} & r_{32} & r_{33} & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_{w} \\
Y_{w} \\
Z_{w} \\
1
\end{bmatrix}
\end{align*}
\f]
@note
- An example of how to use solvePnP for planar augmented reality can be found at
opencv_source_code/samples/python/plane_ar.py
- If you are using Python:
- Numpy array slices won't work as input because solvePnP requires contiguous
arrays (enforced by the assertion using cv::Mat::checkVector() around line 55 of
modules/calib3d/src/solvepnp.cpp version 2.4.9)
- The P3P algorithm requires image points to be in an array of shape (N,1,2) due
to its calling of cv::undistortPoints (around line 75 of modules/calib3d/src/solvepnp.cpp version 2.4.9)
which requires 2-channel information.
- Thus, given some data D = np.array(...) where D.shape = (N,M), in order to use a subset of
it as, e.g., imagePoints, one must effectively copy it into a new array: imagePoints =
np.ascontiguousarray(D[:,:2]).reshape((N,1,2))
- The methods **SOLVEPNP_DLS** and **SOLVEPNP_UPNP** cannot be used as the current implementations are
unstable and sometimes give completely wrong results. If you pass one of these two
flags, **SOLVEPNP_EPNP** method will be used instead.
- The minimum number of points is 4 in the general case. In the case of **SOLVEPNP_P3P** and **SOLVEPNP_AP3P**
methods, it is required to use exactly 4 points (the first 3 points are used to estimate all the solutions
of the P3P problem, the last one is used to retain the best solution that minimizes the reprojection error).
- With **SOLVEPNP_ITERATIVE** method and `useExtrinsicGuess=true`, the minimum number of points is 3 (3 points
are sufficient to compute a pose but there are up to 4 solutions). The initial solution should be close to the
global solution to converge.
- With **SOLVEPNP_IPPE** input points must be >= 4 and object points must be coplanar.
- With **SOLVEPNP_IPPE_SQUARE** this is a special case suitable for marker pose estimation.
Number of input points must be 4. Object points must be defined in the following order:
- point 0: [-squareLength / 2, squareLength / 2, 0]
- point 1: [ squareLength / 2, squareLength / 2, 0]
- point 2: [ squareLength / 2, -squareLength / 2, 0]
- point 3: [-squareLength / 2, -squareLength / 2, 0]
*/
CV_EXPORTS_W int solvePnPGeneric( InputArray objectPoints, InputArray imagePoints,
InputArray cameraMatrix, InputArray distCoeffs,
OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs,
bool useExtrinsicGuess = false, SolvePnPMethod flags = SOLVEPNP_ITERATIVE,
InputArray rvec = noArray(), InputArray tvec = noArray(),
OutputArray reprojectionError = noArray() );
4. 源码解析
文件位置 modules\calib3d\src\solvepnp.cpp
int solvePnPGeneric( InputArray _opoints, InputArray _ipoints,
InputArray _cameraMatrix, InputArray _distCoeffs,
OutputArrayOfArrays _rvecs, OutputArrayOfArrays _tvecs,
bool useExtrinsicGuess, SolvePnPMethod flags,
InputArray _rvec, InputArray _tvec,
OutputArray reprojectionError) {
CV_INSTRUMENT_REGION();
Mat opoints = _opoints.getMat(), ipoints = _ipoints.getMat();
int npoints = std::max(opoints.checkVector(3, CV_32F), opoints.checkVector(3, CV_64F));
CV_Assert( ( (npoints >= 4) || (npoints == 3 && flags == SOLVEPNP_ITERATIVE && useExtrinsicGuess) )
&& npoints == std::max(ipoints.checkVector(2, CV_32F), ipoints.checkVector(2, CV_64F)) );
opoints = opoints.reshape(3, npoints);
ipoints = ipoints.reshape(2, npoints);
if( flags != SOLVEPNP_ITERATIVE )
useExtrinsicGuess = false;
if (useExtrinsicGuess)
CV_Assert( !_rvec.empty() && !_tvec.empty() );
if( useExtrinsicGuess )
{
int rtype = _rvec.type(), ttype = _tvec.type();
Size rsize = _rvec.size(), tsize = _tvec.size();
CV_Assert( (rtype == CV_32FC1 || rtype == CV_64FC1) &&
(ttype == CV_32FC1 || ttype == CV_64FC1) );
CV_Assert( (rsize == Size(1, 3) || rsize == Size(3, 1)) &&
(tsize == Size(1, 3) || tsize == Size(3, 1)) );
}
Mat cameraMatrix0 = _cameraMatrix.getMat();
Mat distCoeffs0 = _distCoeffs.getMat();
Mat cameraMatrix = Mat_<double>(cameraMatrix0);
Mat distCoeffs = Mat_<double>(distCoeffs0);
vector<Mat> vec_rvecs, vec_tvecs;
if (flags == SOLVEPNP_EPNP || flags == SOLVEPNP_DLS || flags == SOLVEPNP_UPNP)
{
Mat undistortedPoints;
undistortPoints(ipoints, undistortedPoints, cameraMatrix, distCoeffs);
epnp PnP(cameraMatrix, opoints, undistortedPoints);
Mat rvec, tvec, R;
PnP.compute_pose(R, tvec);
Rodrigues(R, rvec);
vec_rvecs.push_back(rvec);
vec_tvecs.push_back(tvec);
}
else if (flags == SOLVEPNP_P3P || flags == SOLVEPNP_AP3P)
{
vector<Mat> rvecs, tvecs;
solveP3P(opoints, ipoints, _cameraMatrix, _distCoeffs, rvecs, tvecs, flags);
vec_rvecs.insert(vec_rvecs.end(), rvecs.begin(), rvecs.end());
vec_tvecs.insert(vec_tvecs.end(), tvecs.begin(), tvecs.end());
}
else if (flags == SOLVEPNP_ITERATIVE)
{
Mat rvec, tvec;
if (useExtrinsicGuess)
{
rvec = _rvec.getMat();
tvec = _tvec.getMat();
}
else
{
rvec.create(3, 1, CV_64FC1);
tvec.create(3, 1, CV_64FC1);
}
CvMat c_objectPoints = cvMat(opoints), c_imagePoints = cvMat(ipoints);
CvMat c_cameraMatrix = cvMat(cameraMatrix), c_distCoeffs = cvMat(distCoeffs);
CvMat c_rvec = cvMat(rvec), c_tvec = cvMat(tvec);
cvFindExtrinsicCameraParams2(&c_objectPoints, &c_imagePoints, &c_cameraMatrix,
(c_distCoeffs.rows && c_distCoeffs.cols) ? &c_distCoeffs : 0,
&c_rvec, &c_tvec, useExtrinsicGuess );
vec_rvecs.push_back(rvec);
vec_tvecs.push_back(tvec);
}
else if (flags == SOLVEPNP_IPPE)
{
CV_DbgAssert(isPlanarObjectPoints(opoints, 1e-3));
Mat undistortedPoints;
undistortPoints(ipoints, undistortedPoints, cameraMatrix, distCoeffs);
IPPE::PoseSolver poseSolver;
Mat rvec1, tvec1, rvec2, tvec2;
float reprojErr1, reprojErr2;
try
{
poseSolver.solveGeneric(opoints, undistortedPoints, rvec1, tvec1, reprojErr1, rvec2, tvec2, reprojErr2);
if (reprojErr1 < reprojErr2)
{
vec_rvecs.push_back(rvec1);
vec_tvecs.push_back(tvec1);
vec_rvecs.push_back(rvec2);
vec_tvecs.push_back(tvec2);
}
else
{
vec_rvecs.push_back(rvec2);
vec_tvecs.push_back(tvec2);
vec_rvecs.push_back(rvec1);
vec_tvecs.push_back(tvec1);
}
}
catch (...) { }
}
else if (flags == SOLVEPNP_IPPE_SQUARE)
{
CV_Assert(npoints == 4);
#if defined _DEBUG || defined CV_STATIC_ANALYSIS
double Xs[4][3];
if (opoints.depth() == CV_32F)
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 3; j++)
{
Xs[i][j] = opoints.ptr<Vec3f>(0)[i](j);
}
}
}
else
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 3; j++)
{
Xs[i][j] = opoints.ptr<Vec3d>(0)[i](j);
}
}
}
const double equalThreshold = 1e-9;
//Z must be zero
for (int i = 0; i < 4; i++)
{
CV_DbgCheck(Xs[i][2], approxEqual(Xs[i][2], 0, equalThreshold), "Z object point coordinate must be zero!");
}
//Y0 == Y1 && Y2 == Y3
CV_DbgCheck(Xs[0][1], approxEqual(Xs[0][1], Xs[1][1], equalThreshold), "Object points must be: Y0 == Y1!");
CV_DbgCheck(Xs[2][1], approxEqual(Xs[2][1], Xs[3][1], equalThreshold), "Object points must be: Y2 == Y3!");
//X0 == X3 && X1 == X2
CV_DbgCheck(Xs[0][0], approxEqual(Xs[0][0], Xs[3][0], equalThreshold), "Object points must be: X0 == X3!");
CV_DbgCheck(Xs[1][0], approxEqual(Xs[1][0], Xs[2][0], equalThreshold), "Object points must be: X1 == X2!");
//X1 == Y1 && X3 == Y3
CV_DbgCheck(Xs[1][0], approxEqual(Xs[1][0], Xs[1][1], equalThreshold), "Object points must be: X1 == Y1!");
CV_DbgCheck(Xs[3][0], approxEqual(Xs[3][0], Xs[3][1], equalThreshold), "Object points must be: X3 == Y3!");
#endif
Mat undistortedPoints;
undistortPoints(ipoints, undistortedPoints, cameraMatrix, distCoeffs);
IPPE::PoseSolver poseSolver;
Mat rvec1, tvec1, rvec2, tvec2;
float reprojErr1, reprojErr2;
try
{
poseSolver.solveSquare(opoints, undistortedPoints, rvec1, tvec1, reprojErr1, rvec2, tvec2, reprojErr2);
if (reprojErr1 < reprojErr2)
{
vec_rvecs.push_back(rvec1);
vec_tvecs.push_back(tvec1);
vec_rvecs.push_back(rvec2);
vec_tvecs.push_back(tvec2);
}
else
{
vec_rvecs.push_back(rvec2);
vec_tvecs.push_back(tvec2);
vec_rvecs.push_back(rvec1);
vec_tvecs.push_back(tvec1);
}
} catch (...) { }
}
/*else if (flags == SOLVEPNP_DLS)
{
Mat undistortedPoints;
undistortPoints(ipoints, undistortedPoints, cameraMatrix, distCoeffs);
dls PnP(opoints, undistortedPoints);
Mat rvec, tvec, R;
bool result = PnP.compute_pose(R, tvec);
if (result)
{
Rodrigues(R, rvec);
vec_rvecs.push_back(rvec);
vec_tvecs.push_back(tvec);
}
}
else if (flags == SOLVEPNP_UPNP)
{
upnp PnP(cameraMatrix, opoints, ipoints);
Mat rvec, tvec, R;
PnP.compute_pose(R, tvec);
Rodrigues(R, rvec);
vec_rvecs.push_back(rvec);
vec_tvecs.push_back(tvec);
}*/
else
CV_Error(CV_StsBadArg, "The flags argument must be one of SOLVEPNP_ITERATIVE, SOLVEPNP_P3P, SOLVEPNP_EPNP or SOLVEPNP_DLS");
CV_Assert(vec_rvecs.size() == vec_tvecs.size());
int solutions = static_cast<int>(vec_rvecs.size());
int depthRot = _rvecs.fixedType() ? _rvecs.depth() : CV_64F;
int depthTrans = _tvecs.fixedType() ? _tvecs.depth() : CV_64F;
_rvecs.create(solutions, 1, CV_MAKETYPE(depthRot, _rvecs.fixedType() && _rvecs.kind() == _InputArray::STD_VECTOR ? 3 : 1));
_tvecs.create(solutions, 1, CV_MAKETYPE(depthTrans, _tvecs.fixedType() && _tvecs.kind() == _InputArray::STD_VECTOR ? 3 : 1));
for (int i = 0; i < solutions; i++)
{
Mat rvec0, tvec0;
if (depthRot == CV_64F)
rvec0 = vec_rvecs[i];
else
vec_rvecs[i].convertTo(rvec0, depthRot);
if (depthTrans == CV_64F)
tvec0 = vec_tvecs[i];
else
vec_tvecs[i].convertTo(tvec0, depthTrans);
if (_rvecs.fixedType() && _rvecs.kind() == _InputArray::STD_VECTOR)
{
Mat rref = _rvecs.getMat_();
if (_rvecs.depth() == CV_32F)
rref.at<Vec3f>(0,i) = Vec3f(rvec0.at<float>(0,0), rvec0.at<float>(1,0), rvec0.at<float>(2,0));
else
rref.at<Vec3d>(0,i) = Vec3d(rvec0.at<double>(0,0), rvec0.at<double>(1,0), rvec0.at<double>(2,0));
}
else
{
_rvecs.getMatRef(i) = rvec0;
}
if (_tvecs.fixedType() && _tvecs.kind() == _InputArray::STD_VECTOR)
{
Mat tref = _tvecs.getMat_();
if (_tvecs.depth() == CV_32F)
tref.at<Vec3f>(0,i) = Vec3f(tvec0.at<float>(0,0), tvec0.at<float>(1,0), tvec0.at<float>(2,0));
else
tref.at<Vec3d>(0,i) = Vec3d(tvec0.at<double>(0,0), tvec0.at<double>(1,0), tvec0.at<double>(2,0));
}
else
{
_tvecs.getMatRef(i) = tvec0;
}
}
if (reprojectionError.needed())
{
int type = (reprojectionError.fixedType() || !reprojectionError.empty())
? reprojectionError.type()
: (max(_ipoints.depth(), _opoints.depth()) == CV_64F ? CV_64F : CV_32F);
reprojectionError.create(solutions, 1, type);
CV_CheckType(reprojectionError.type(), type == CV_32FC1 || type == CV_64FC1,
"Type of reprojectionError must be CV_32FC1 or CV_64FC1!");
Mat objectPoints, imagePoints;
if (opoints.depth() == CV_32F)
{
opoints.convertTo(objectPoints, CV_64F);
}
else
{
objectPoints = opoints;
}
if (ipoints.depth() == CV_32F)
{
ipoints.convertTo(imagePoints, CV_64F);
}
else
{
imagePoints = ipoints;
}
for (size_t i = 0; i < vec_rvecs.size(); i++)
{
vector<Point2d> projectedPoints;
projectPoints(objectPoints, vec_rvecs[i], vec_tvecs[i], cameraMatrix, distCoeffs, projectedPoints);
double rmse = norm(Mat(projectedPoints, false), imagePoints, NORM_L2) / sqrt(2*projectedPoints.size());
Mat err = reprojectionError.getMat();
if (type == CV_32F)
{
err.at<float>(static_cast<int>(i)) = static_cast<float>(rmse);
}
else
{
err.at<double>(static_cast<int>(i)) = rmse;
}
}
}
return solutions;
}






















 5795
5795

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










