【论文阅读】On-Manifold Preintegration

原创已于 2023-06-11 15:28:27 修改 · 1.9k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#自动驾驶 #机器学习 #算法

于 2022-03-13 17:35:14 首次发布

DSO/SVO 专栏收录该内容

18 篇文章

订阅专栏

本文详细介绍了预积分技术在实时视觉惯性里程计（Visual-Inertial Odometry, VIO）中的应用。预积分将一段时间内的惯性测量数据累积处理，避免频繁优化带来的计算开销。通过线性化模型处理零偏估计变化，简化了预积分的计算，并保持了系统的高效性。预积分的噪声模型和雅可比矩阵的计算也得到了阐述，这对于构建优化框架至关重要。

【论文阅读】On-Manifold Preintegration

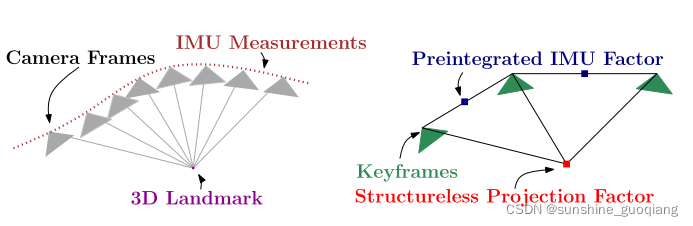
本文介绍了预积分的技术细节。

C. Forster, L. Carlone, F. Dellaert, D. Scaramuzza. On-Manifold Preintegration for Real-Time Visual-Inertial Odometry.IEEE Transactions on Robotics, 33(1), 1-21, 2017.

在这里插入图片描述
以上过程与我们在IMU测量方程和噪声方程中已有描述。当然，我们完全可以用这种约束来构建图优化，对IMU相关的问题进行求解。但是这组方程刻画的时间太短，或者说，IMU的测量频率太高。我们并不希望优化过程随着IMU数据进行调用，那样太浪费计算资源。于是，预积分方法应运而生，它可以把一段时间的IMU数据累计起来统一处理。现在介绍如何在关键帧之间对IMU进行预积分。

我们不妨假设从关键帧 i 和 j 之间的IMU数据被累计起来，这个过程通常可以持续若干秒钟。这种被累计起来的观测被称为预积分[7]。当然，如果我们使用不同形式的运动学，得到的预积分形式也是不同的。本文主要使用 [SO(3)+5] 的方式来推导预积分。那么，在 [k] 至 [j] 过程中，我们可以把上式中的变量累计起来，得到：
在这里插入图片描述
这种改变实际上只是计算了某种从 [i] 到 [j] 的“差值”。这个定义在计算上有一些有趣的性质：

我们不妨考虑从 [i] 时刻出发，此时这三个量都为零。在 [i+1] 时刻，我们计算出 [Delta Ri,i+1] ,[Delta vi,i+1] 和 [Delta pi,i+1] 。而在 [i+2] 时刻时，由于这三个式子都是累乘或累加的形式，只需在 [i+1] 时刻的结果之上，加上第 [i+2] 时刻的测量值即可。这在计算层面带来了很大的便利。进一步，我们还会发现这种性质对后续计算各种雅可比矩阵都非常方便。
上述所有计算都和 [ Ri] 的取值无关。即使 [ Ri] 的估计值发生改变，这些量也无需重新计算。这又是非常方便的一个特性。
不过，如果零偏 [b_a,k] 或 [b_g,k] 发生变化，那么上述式子理论上还是需要重新计算。然而，我们也可以通过“修正”而非“重新计算”的思路，来调整我们的预积分量。
请注意，预积分量并没有直接的物理含义。尽管符号上用了 [Delta v] 之类的样子，但它并不表示某两个速度或位置上的偏差。它只是如此定义而已。当然，从量纲上来说，应该与角度、速度、位移对应。
同样地，由于预积分量不是直接的物理量，这种“测量模型”的噪声也必须从原始的IMU噪声推导而来。
从这几个问题出发，我们来介绍如何构造预积分的测量模型、噪声模型，以及它对各种状态变量的雅可比应该如何方便地计算。

构建预积分测量模型

由前面的讨论可见，预积分内部带有IMU的零偏量，因此不可避免地会依赖此时的零偏量估计。为了处理这种依赖，我们对预积分定义作一些工程上的调整：

我们首先认为 [i] 时刻的零偏是固定的，并且在整个预积分计算过程中也都是固定的。
我们作出预积分对零偏量的一阶线性化模型，即，舍弃对零偏量的高阶项。
当零偏估计发生改变时，用这个线性模型来修正预积分。

在这里插入图片描述

此式是高斯随机变量的线性组合，它的结果依然是高斯的。同时，由于预积分的累加特性，预测分观测量的噪声也会随着时间不断累加。我们可以这样提问：能否用第 [j-1] 时刻的噪声来计算第 [j] 时刻的噪声？如果可以，那么程序实现也会更加简单。

答案显然是肯定的。由于上式是累加形式的，很容易将其写成递推的形式：
在这里插入图片描述
矩阵形式更清晰地显示了几个噪声项之间累计递推关系。由于它们的累加关系，在程序实现中也十分便捷。
零偏的更新

先前的讨论都假设了在 [公式] 时刻的IMU零偏恒定不变，当然这都是为了方便后续的计算。然而在实际的图优化中，我们经常会对状态变量（优化变量）进行更新。那么，理论上来讲，如果IMU零偏发生了变化，预积分应该重新计算，因为预积分的每一步都用到了 [i] 时刻的IMU零偏。但是实际操作过程中，我们也可以选用一种讨巧的做法：假定预积分观测是随零偏线性变化的，虽然实际上并不是线性变化的，但我们总可以对一个复杂函数做线性化并保留一阶项,然后在原先的观测量上进行修正。
在这里插入图片描述

参考文献：

[1]. C.Forster, L.Carlone, F.Dellaert,and D.Scaramuzza “IMU preintegration on manifold for efficient visual inertial maximum a posteriori estimation,” in Robotics: Science and Systems XI, no. EPFLCONF214687, 2015.

[2]. L. Chang, X. Niu, and T. Liu, “GNSS/imu/odo/lidarslam integrated navigation system using imu/odo pre integration,” Sensors, vol. 20, no. 17, p. 4702, 2020.

[3]. Z. Yuan, D. Zhu, C. Chi, J. Tang, C. Liao, and X. Yang, “Visual inertial state estimation with preintegration correction for robust mobile augmented reality,” in Proceedings of the 27th ACM International Conference on Multimedia, pp. 1410–1418, 2019.

[4]. K. Eckenhoff, P. Geneva, and G. Huang, “Closedform preintegration methods for graphbased visual-inertial navigation,” The International Journal of Robotics Research, vol. 38, no. 5, pp. 563–586, 2019.

[5]. R. M. Murray, Z. Li, and S. S. Sastry, A mathematical introduction to robotic manipulation. CRC press, 2017.

[6]. J. L. Crassidis, “Sigmapoint Kalman filtering for integrated GPS and inertial navigation,” IEEE Transactions on Aerospace and Electronic Systems, vol. 42, no. 2, pp. 750–756, 2006.

[7]. T.Luptonand, S.Sukkarieh, “Visual inertial aided navigation for highdynamic motion in built environments without initial conditions,” IEEE Transactions on Robotics, vol. 28, no. 1, pp. 61–76, 2011.

[8]. S.Leutenegger, S.Lynen, M.Bosse, R.Siegwart, and P.Furgale, “Keyframe based visual-inertial odometry using nonlinear optimization,” The International Journal of Robotics Research, vol. 34, no. 3, pp. 314–334, 2015.
[9]. https://zhuanlan.zhihu.com/p/388859808
[10]. https://zhuanlan.zhihu.com/p/108203458
[11]. https://blog.youkuaiyun.com/weixin_41230454/article/details/84343506
[12]. https://lgg2018.com/2019/12/15/imu%e9%a2%84%e7%a7%af%e5%88%86/
[13]. IMU 预积分推导
[14] IMU预积分–详细推导过程