【OpenCV】中的鱼眼相机及其标定

1. 鱼眼镜头特性与镜头分类

普通镜头和针孔相机在数学模型上可以等价对待，都是射影变换（Perspective transform）；
鱼眼镜头受到水下斯涅耳窗口现象的启发，采用不同的投影方式，来得到极大的视场角；
鱼眼镜头常用的投影方式包括等距投影、等积投影、体视投影、正交投影等；

2. 鱼眼镜头与呈像相似性

对日常生活、甚至一些艺术创作、科学研究来说，保持像与物的相似是一件好事。偏离相似性，我们就说镜头有了畸变，大多数时候，我们并不希望镜头有畸变，甚至在设计镜头的时候，专门针对「偏离相似性」——也就是镜头畸变进行校正。不过在一些特殊的场合，我们也需要特意偏离物像的相似性，以求得其他方面的便利。

一个极好的例子是气象科学中，对天空云量的测量。在这个场景中，人们希望能够获得尽可能大的视野范围，最好是直接把整个天空一次性拍摄下来——这就要求镜头能够达到 180° 的视场角。容易想到，我们可以把天空和云看做分布于一个半径无穷大的球面上，也就是说，我们要把一个（半）球面的场景尽可能全地记录、拍摄下来。普通的超广角镜头难以完成这样的任务。

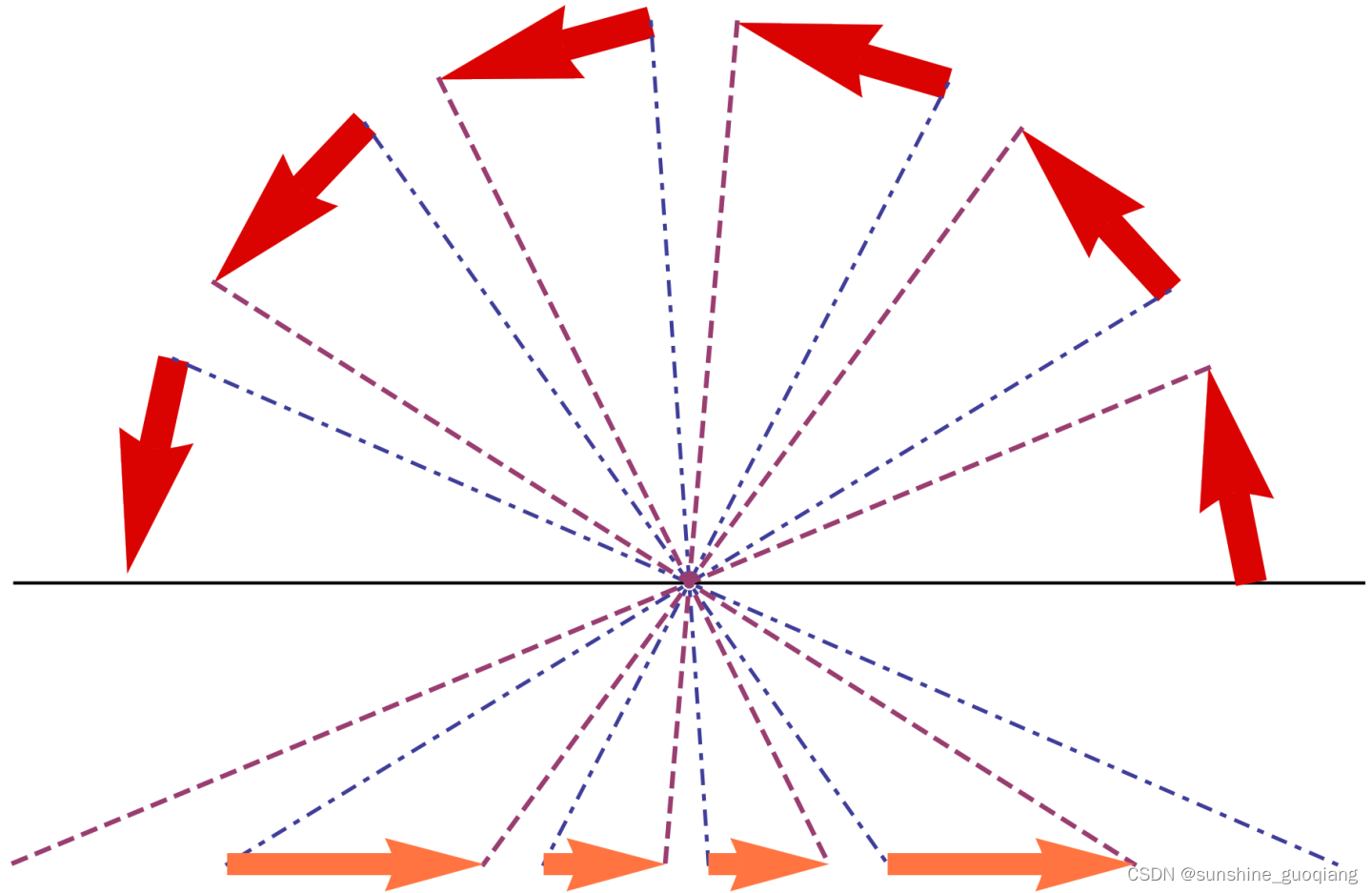
如图所示，面对半球场景，普通的超广角镜头只能记录中间的部分，越靠近边缘，透视变形越大。图中同样长度的红色箭头，靠近边缘的话，经过镜头成像之后就变得更长；对于极端接近边缘的物体，普通的广角镜头是无法成像记录的。这种情况下，追求「相似性」反而成为了障碍。

既然追求「相似性」的普通镜头难以胜任这样的任务场景，那么我们放弃相似性是不是就可以完成任务了呢？比如，对于靠近边缘的光线，我们不再要求他继续保持出射角与入射角相等，而是弯折一些，这样不就可以记录更大的视角范围了吗？而且物体的长度也不至于被拉伸得很厉害。

人们想到了水下的鱼。由于水的折射率比空气大，光线从空气进入水中，折射角比入射角更小，并且入射角越大，这个变小的程度也越大。这正好是我们所需要的特性。由于这个特性，使得水下的鱼在向上看的时候，能一眼看到整个水面上的这个半球形空间；这整个空间的影像，都被「扭曲」、「压缩」到了一个半顶角约为 48° 的锥形内。

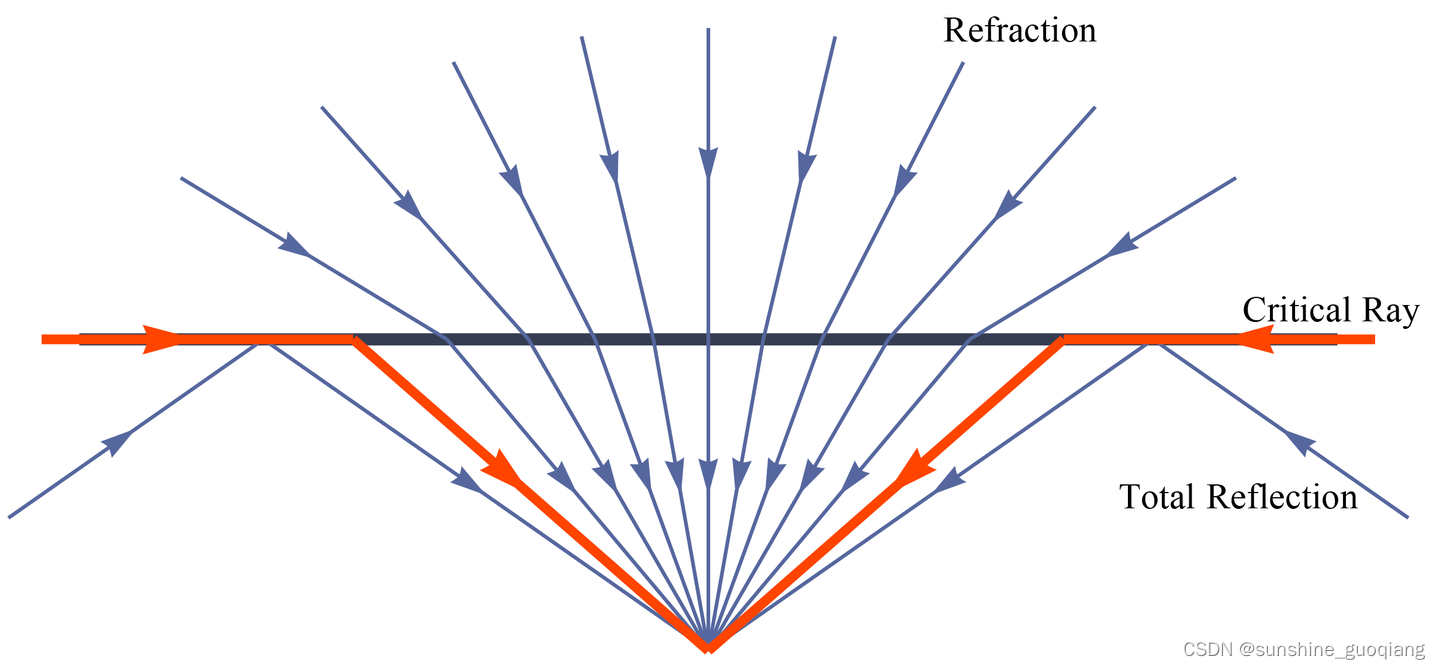
空气-水界面处的光线折射与全反射）

在这个锥形空间内部，是来自水面上的空间的光线，在这个锥形外部，是来自水面下景色的反射。也就是说，在水下向上看，在一个圈之外，只能看到水底的景色；所有水面上的景色，都被压缩在一个圈内。这个圈，也叫「斯涅耳窗口（Snell’s window）」

3. 鱼眼镜头及投影方式

从数学上来说，普通的镜头成像相当于进行了一次射影变换。那么鱼眼镜头是一个什么变换呢？我们来看看，鱼眼镜头的变换，需要有什么样的特性。

3.1

**第一,视角要大。**或者说，对于某一个入射角，经过镜头之后射向成像面的出射角，一定是要小于入射角的。否则没办法在一个相对较小的范围内记录极大的视角。

**第二，最好这个变换有比较良好的性质。**什么叫「良好的性质」？比如说普通镜头对应的射影变换，就有良好的性质，经过射影变换后，很多几何特征能保持不变，直线还是直线、圆锥曲线还是圆锥曲线。我们希望鱼眼镜头对应的这个变换，也能够保持一些几何特征不变。比如，变换前后，圆还是圆；比如，变换前后，一块空间所占的立体角不变。

第三，最好这个变换的形式比较简单。简单的形式方便让人从成像中直接观测、推断，而不用经过复杂的运算才能看出拍的是个什么东西。

我们来看看，满足这三个条件的情况下，鱼眼镜头可以有什么样的变换形式（我们把这种变换叫做投影，Projection）。为了直观地感受不同投影方式带来的差异，我写了一个简单的图形渲染器。受到 WiKi Fisheye lens 中的场景启发，我设置了一个差不多的场景，是一个直筒型的管道，管道壁上有规则的颜色格子。在这个场景中用不同的投影方式去模拟鱼眼镜头拍摄的图像，以便让大家有一个直观的感受。

（模拟场景管道内，普通 14mm 超广角不同视角拍摄的效果）

斯涅耳窗投影，也就是真的去模仿水下鱼类向上看的时候的场景，我把这个投影方式叫做斯涅耳窗投影。用公式表达出射角和入射角之间的关系是 θ′=sin−1⁡(sin⁡θ/n)，其中 θ 是入射角，θ′ 是出射角，n 是水的折射率。很显然，这种投影方式最大的视角不会超过 180°。这种投影方式没什么特别的用处，在这里也只是作为最初的起点。现实中我从来没见哪个鱼眼镜头是用这种投影方式的。

（斯涅耳窗投影效果）

3.2 投影函数

鱼眼相机按照一定的投影函数来设计,尽可能大的场景投影到有限的图像平面内。根据投影函数的不同，鱼眼相机的设计模型大致能被分为四种：等积投影模型、等距投影模型、体视投影模型、正交投影模型。下面的四种鱼眼相机的投影模型反映出了空间中的一点P是如何投影到球面上，然后到图像平面上成像的。

3.2.1 等积投影模型

等积投影（Equisolid angle，equal area），也叫等立体角投影。用公式表达物体成像后与画面中心的距离 r 与入射角 θ 之间的关系就是 r=2fsin⁡(θ/2)。

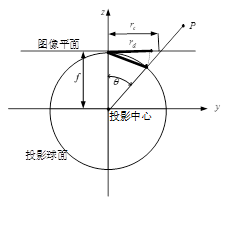
这种投影方式的特征在于，能保持变换前后，物体所占的立体角大小不变。或者说，在半球形空间中，半球面上两个「面积」相同的图案，成像后，在成像平面上的两个图案的面积仍然相同（虽然两者形状不一定相似）。这正是这个投影方式名字的由来。这种特性使得这个投影方式被广泛应用，其中一种场合就是测量全天云量覆盖情况。整个天空中云量覆盖多少，是由云所占的空间立体角的比例决定的。用这种投影方式的镜头，直接对着天空拍一张，在照片中测量一下云所占的像素面积比例，就得到了全天云量覆盖情况。在下图的模拟场景中，圆筒壁上每一列的各个小方格的面积都是相等的。

（等积投影效果）

3.2.2 等距投影模型

等距投影（Equidistance，linear scaled）。这种投影方式的特点是，物体在成像面上离开画面中心的距离，与物体在空间中离开光轴的角度成正比，这个比例系数就是镜头焦距。用公式表达这个距离与角度的关系就是 r=fθ，其中 r 就是物体的像到画面中心的距离，就是入射角，也等于物体在空间中离开光轴的角度。

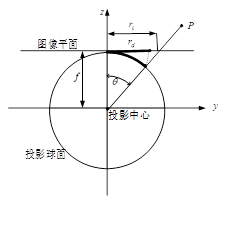
在这种投影变换下，物体离开中心的距离（角度）就是一个重要的几何性质，物体的空间角距离与物体的像在像平面上的平面距离，是成正比的。这也是这个投影方式名称的来源。这种方式的镜头较少，然而更多地用在军事领域。想像一下武器瞄准系统，使用这种投影方式的镜头，不仅监测的视野范围大，而且对于目标的方位角度，只要直接在画面里测量平面距离就可以了，非常方便。在下图的模拟场景中，中间一列的各个小方格的高度都是一样的。

（等距投影效果）

3.2.3 体视投影模型

体视投影（Stereographic，conform）。用公式表达就是 r=2ftan⁡(θ/2)，其中各个符号含义同前。这种投影方式的特点是能保持角度不变，这在数学上是一个非常良好的性质，叫做「保角变换（Conform）」

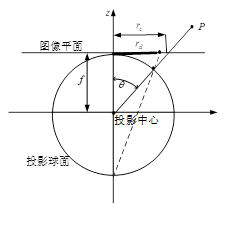
保持角度不变，意思是任何直线相交的角度，在变换之后是保持不变的（虽然直线本身可能变弯曲）。在保角变换下，一个圆仍然还是一个圆（直线可以看做直径无穷大的圆），所以在某种程度上，保角变换也是保持了「形状」不变的。在下面的模拟场景中，圆筒壁上的所有边界线，全部都变成了圆弧；所有线的交角，也都保持了 90° 不变。

（体视投影效果）

3.2.4 正交投影模型

正交投影（Orthographic）。这种投影方式，就像是把整个半球直接拍扁，用公式表达就是 r=sin⁡(θ)。

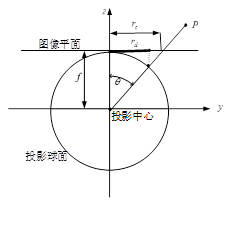
在几种投影方式中，这种投影方式带来的扭曲最大，对边缘物体压缩最厉害，实际很少使用。很显然，这种投影方式的最大视场角也不能大于 180°。

（正交投影效果）
在实际的商品化的民用镜头中，等积投影和等距投影都有不少使用，尤其在科研领域，相对的体视投影的镜头较少，不过也因为这种投影变形较小，还能保持角度不变，使得这种投影方式的镜头拥有相当多的爱好者

4. OpenCV中的鱼眼相机模型标定

OpenCV中使用的模型是由Kannala提出的一种鱼眼相机的一般近似模型。在等距投影模型的基础上提出来的。下面来详细分析其鱼眼相机模型的提出过程。我们可以将鱼眼相机模型的形式统一以等距投影模型的形式来表示，即
$$r_d=f{\theta }_d$$
对实际的鱼眼镜头来说，它们不可能精确地按照投影模型来设计，所以为了方便鱼眼相机的标定，Kannala提出了一种鱼眼相机的一般多项式近似模型。通过前面的四个模型，可以发现 ${\theta }_d$是θ的奇函数，而且将这些式子按泰勒级数展开，发现${\theta }_d$可以用θ 的奇次多项式表示，即
$${\theta }_d=k_0\theta +k_1{\theta }^3+k_2{\theta }^5+k_3{\theta }^7+\cdots$$
为了实际计算的方便，需要确定式中${\theta }_d$取到的次幂数。Kannala提出取式的前五项即取到的九次方，就给出了足够的自由度来很好地近似各种投影模型。 ${\theta }_d$的一次项系数可以为1，于是OpenCV中使用的鱼眼相机模型为：
$${\theta }_d=k_0\theta +k_1{\theta }^3+k_2{\theta }^5+k_3{\theta }^7+k_4{\theta }^9\cdots$$
上式表示的模型是根据四种鱼眼相机投影模型得出的一种通用鱼眼相机多项式模型。这种模型根据θ能够得到 ${\theta }_d$，即通过无畸变图像中的点能够计算出鱼眼图像中的畸变点。这种模型在OpenCV的鱼眼相机标定方法中是适用的，因为OpenCV借助标定板对鱼眼相机进行标定。从空间点到鱼眼图像上的点的变换过程可用式子表示为：
[ Xc &Yc & Zc ] =RX+t
$$\begin{gathered} x_c=X_c/Z_c,y_c=Y_c/Z_c \\ {r}_2={x_c}^2+{y_c}^2 \\ {\theta }_d=k_0\theta +k_1{\theta }^3+k_2{\theta }^5+k_3{\theta }^7+k_4{\theta }^9\cdots \\ {x}_d={\theta }_d/r\ast x_c,y_d={\theta }_d/r\ast y_c \\ \theta =arctan(r) \\ u=f_x\ast x_d+c_x \\ v=f_y\ast y_d+c_y \end{gathered}$$

上面式子中， X表示空间点，$X_c$表示相机坐标系下对应的空间点， R和t分别是两个坐标系之间的旋转矩阵和平移向量，$(u,v{)}^T$ 表示投影到鱼眼图像上的对应点。
OpenCV中对鱼眼相机的标定步骤能够分成四步：
1.求内参矩阵的逆，由于摄像机坐标系的三维点到二维图像平面，需要乘以旋转矩阵R和内参矩阵K。那么反向投影回去则是二维图像坐标乘以 K*R的逆矩阵。

2.将目标图像中的每一个像素点坐标(j,i)，乘以1中求出的逆矩阵iR，转换到摄像机坐标系（_x,_y,_w）,并归一化得到z=1平面下的三维坐标(x,y,1)。

3.求出平面模型下像素点对应鱼眼半球模型下的极坐标(r, theta)。使用LM算法最小化定位的图像点和投影的图像点之间的投影误差；

4.利用鱼眼畸变模型求出拥有畸变时像素点对应的theta_d。

5.利用求出的theta_d值将三维坐标点重投影到二维图像平面得到(u,v)，(u,v)即为目标图像对应的畸变图像中像素点坐标。

6.使用cv::Remap（）函数，根据mapx,mapy取出对应坐标位置的像素值赋值给目标图像，一般采用双线性插值法，得到畸变校正后的目标图像。

标定代码：
链接: https://pan.baidu.com/s/1_-RruxBQ5DqDagB3JHYrMA?pwd=93mt 提取码: 93mt

5. 参考链接

[1] https://ieeexplore.ieee.org/document/1333993
[2] https://ieeexplore.ieee.org/document/1642666/citations#citations
[3] https://docs.opencv.org/4.x/db/d58/group__calib3d__fisheye.html
[4] https://blog.youkuaiyun.com/KYJL888/article/details/81043133
[5] https://blog.youkuaiyun.com/lwx309025167/article/details/103786550
[6] https://blog.youkuaiyun.com/u010128736/article/details/52864024/
[7] https://blog.youkuaiyun.com/qq_16137569/article/details/112398976
[8] https://blog.youkuaiyun.com/waeceo/article/details/51024396
[9] https://docs.opencv.org/3.0-beta/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html#fisheye-initundistortrectifymap