一、数学模型概述
控制系统的数学模型分为
- 控制系统的方框图与信号流图
- 拉普拉斯变换
二、方框图与信号流图
2.1 概述
2.1.1 方框图模型
- 方框图模型的基本概念
- 方框图化简技术
- 方框图化简例子
2.1.2 信号流图模型
- 信号流图模型的基本概念
- 方框图变换为信号流图
- 梅森增益公式
2.2 方框图
2.2.1 概念
方框图是指由单方向的功能框图所组成的一种图解模型,其中的方框表示了系统各元件所对应的传递函数。

- 信号线:信号传递的通道,信号只能沿箭头指向传递。
- 引出点或分支点:对信号进行引出或测量,同一位置引出的信号在数值和性质方面完全相同。
- 相加点或比较点:对两个以上的信号进行加减运算。
- 方框:对信号进行数学变换。
2.2.2 案例
2.2.2.1 直流电机控制系统
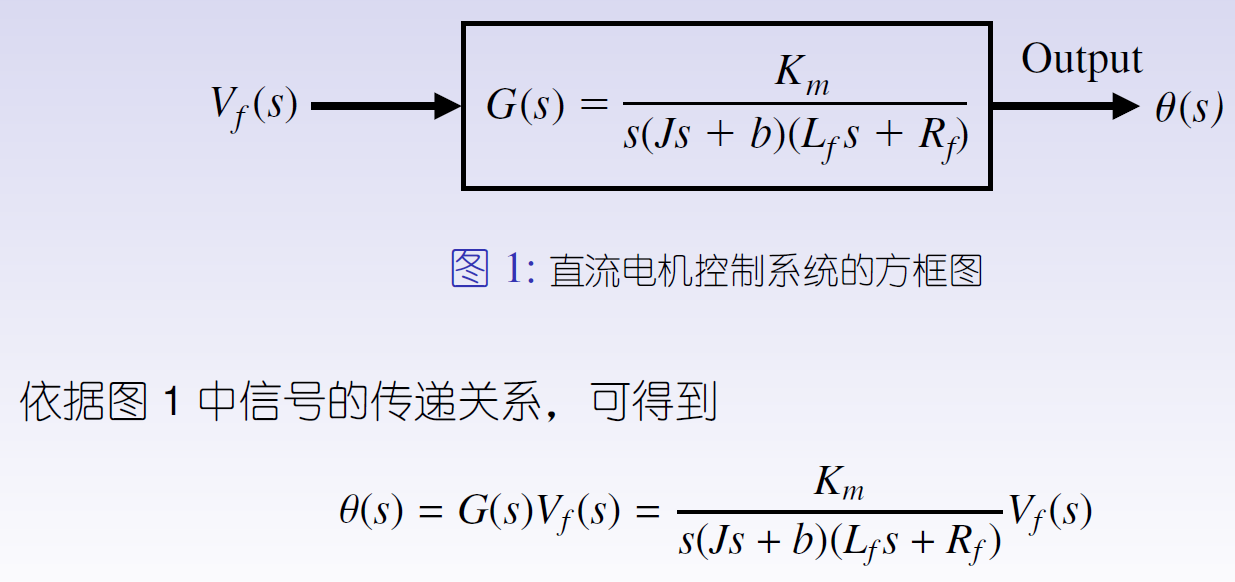
2.2.2.2双输入双输出的控制系统
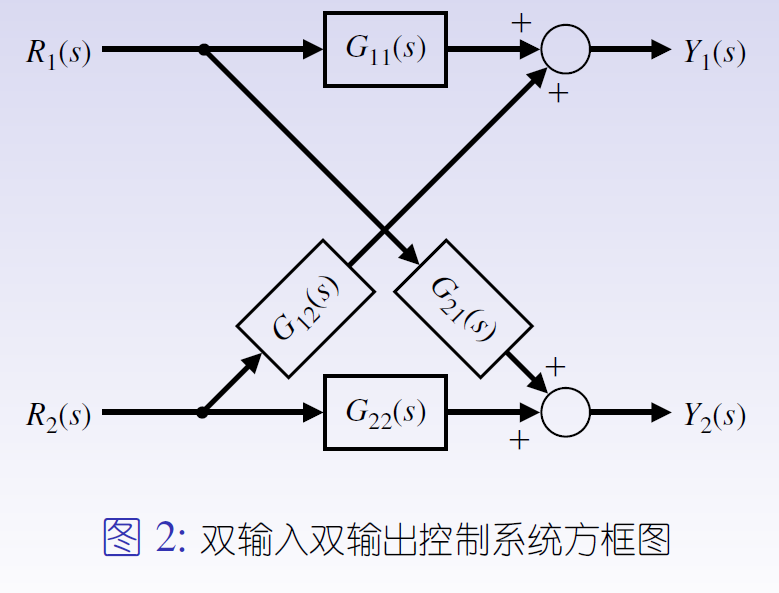
依据信号传递关系,可以得到如下一组线性关系:
Y1(s) = G11(s)R1(s) + G12(s)R2(s)
Y2(s) = G21(s)R1(s) + G22(s)R2(s)
2.2.3 方框图化简技术
2.2.3.1 引子
- Why: 分析一个比较复杂的控制系统,通常需要求解系统的等效传递函数,因此需要用到方框图化简技术。
- what: 方框图基本连接方式只有三种:串联、并联和反馈。
- 原则: 变换前后变量关系保持等效。
2.2.3.2 化简规则

若细分具体的化简实操规则,有如下8条
- ①方框串联
- ②方框并联
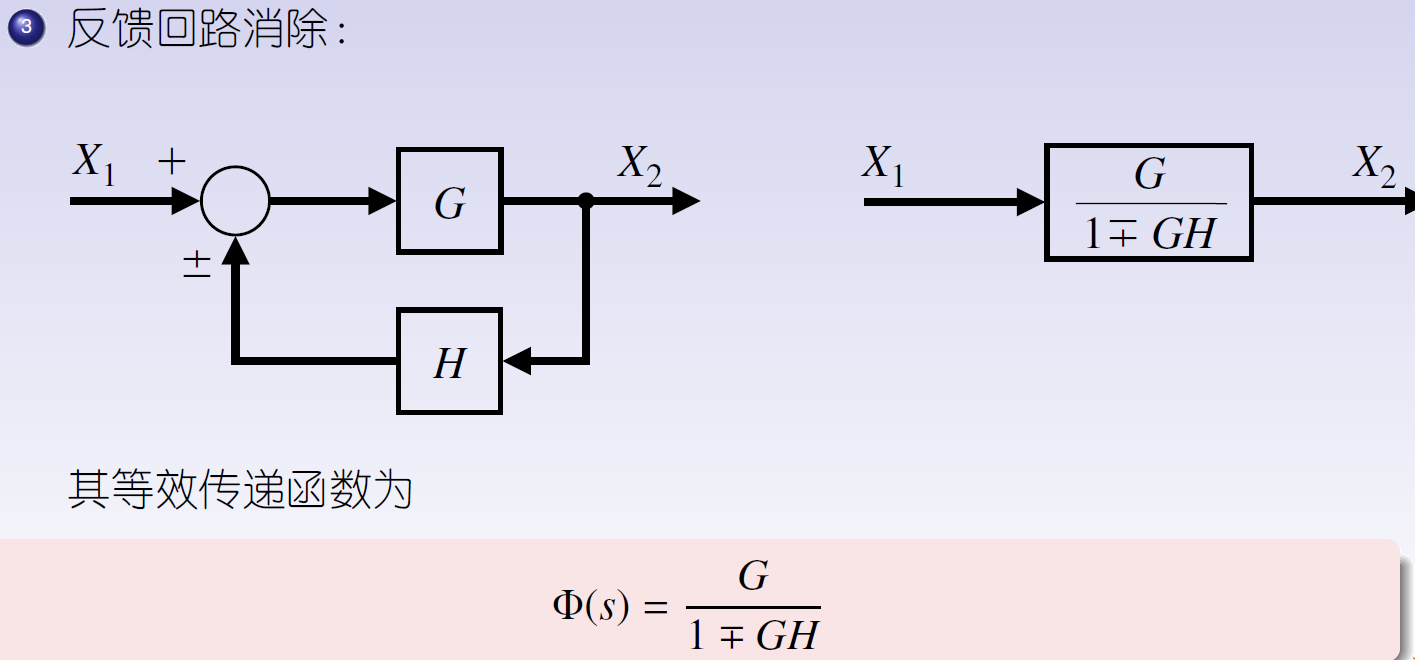
- ③反馈回路消除
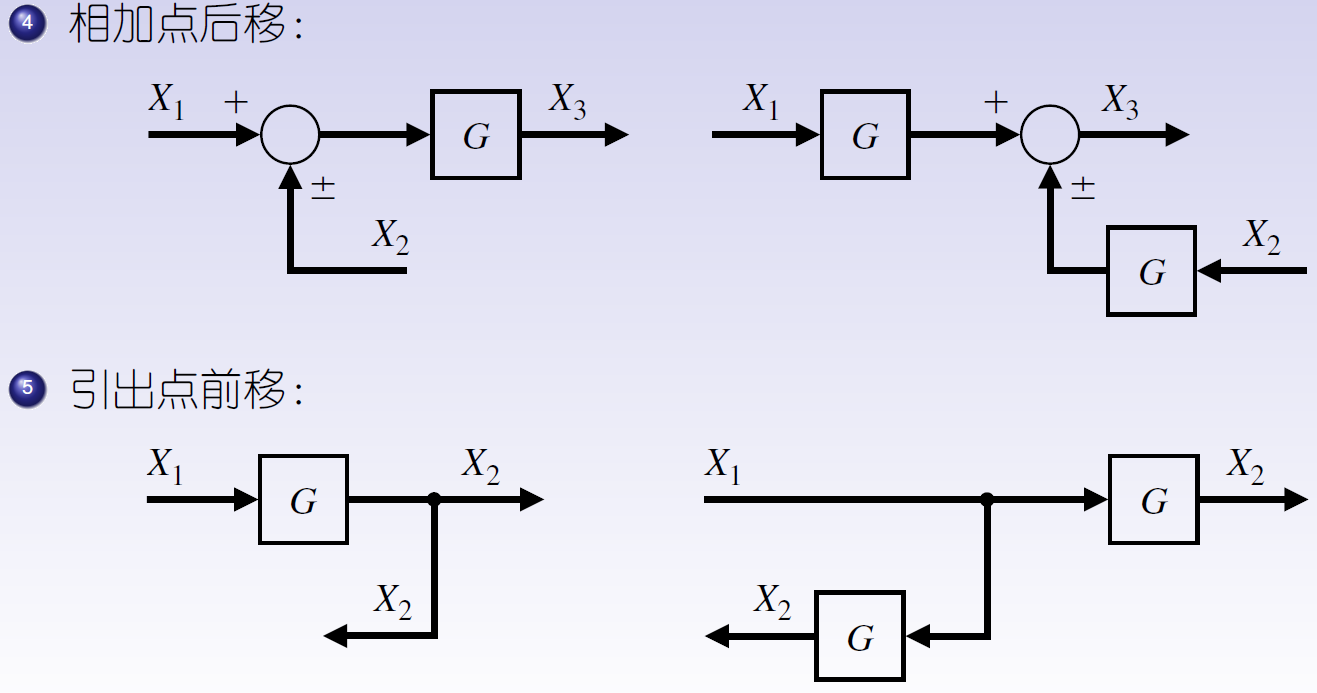
- ④相加点后移
- ⑤引出点前移
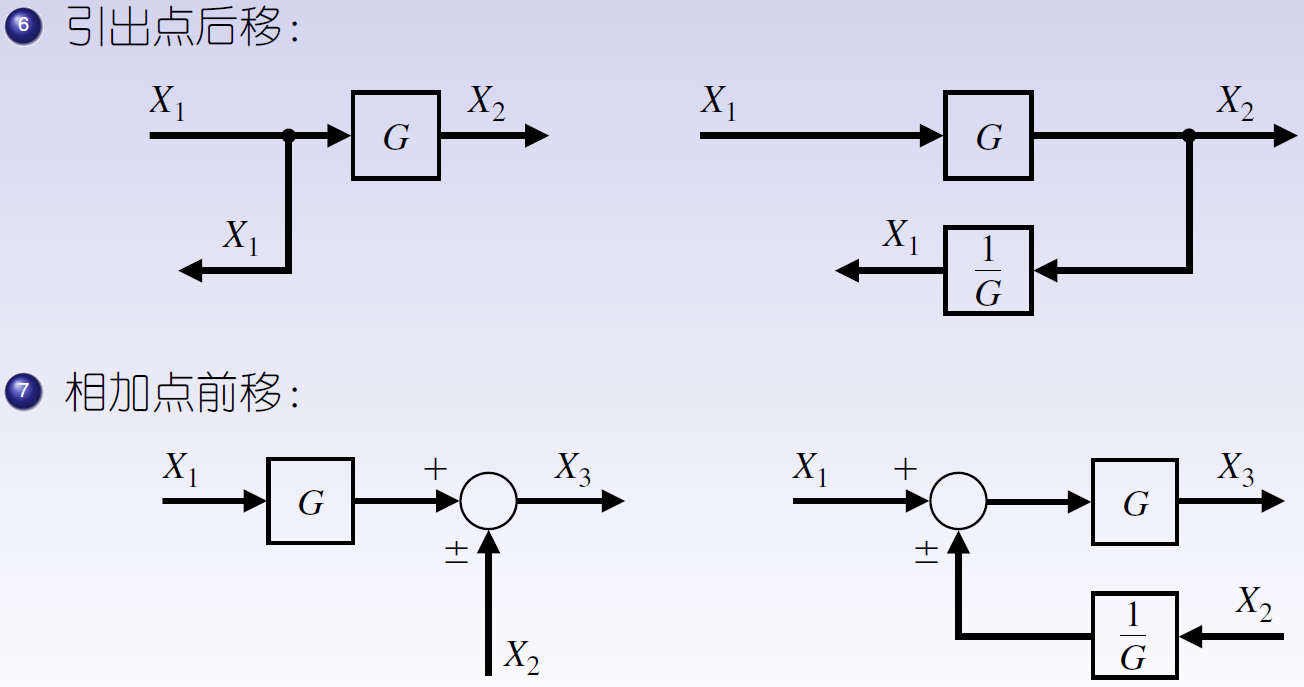
- ⑥引出点后移
- ⑦相加点前移
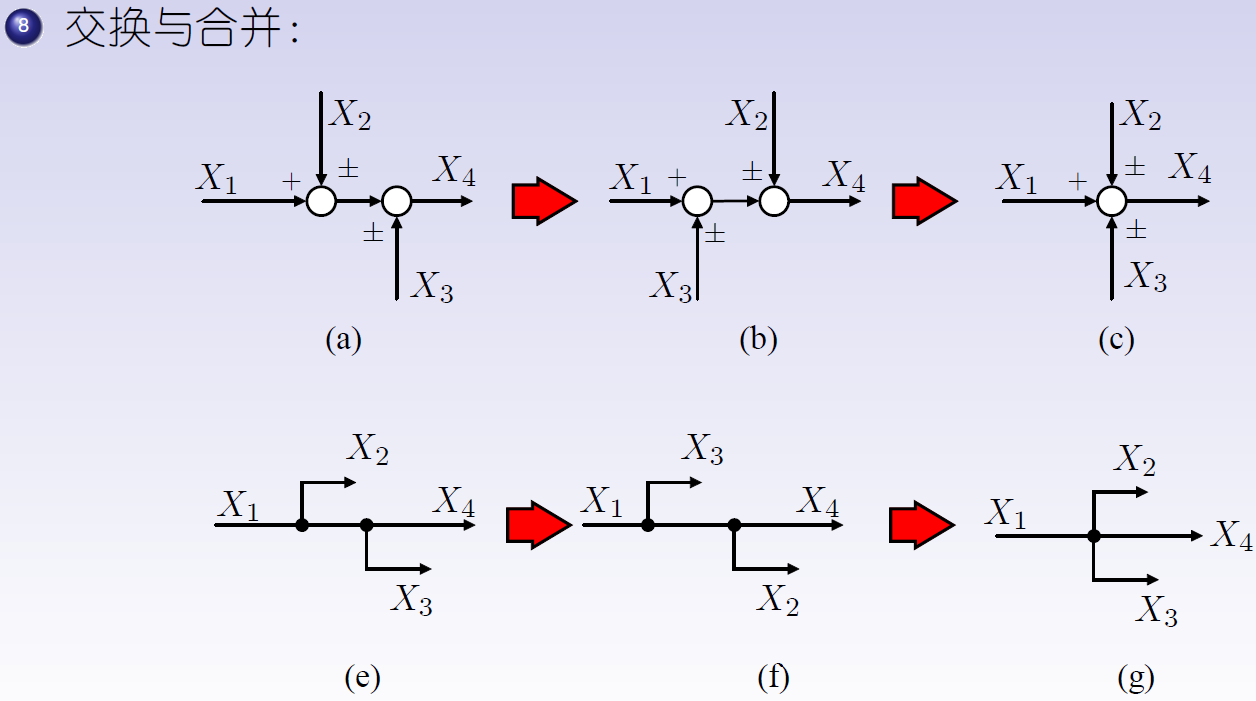
- ⑧交换与合并
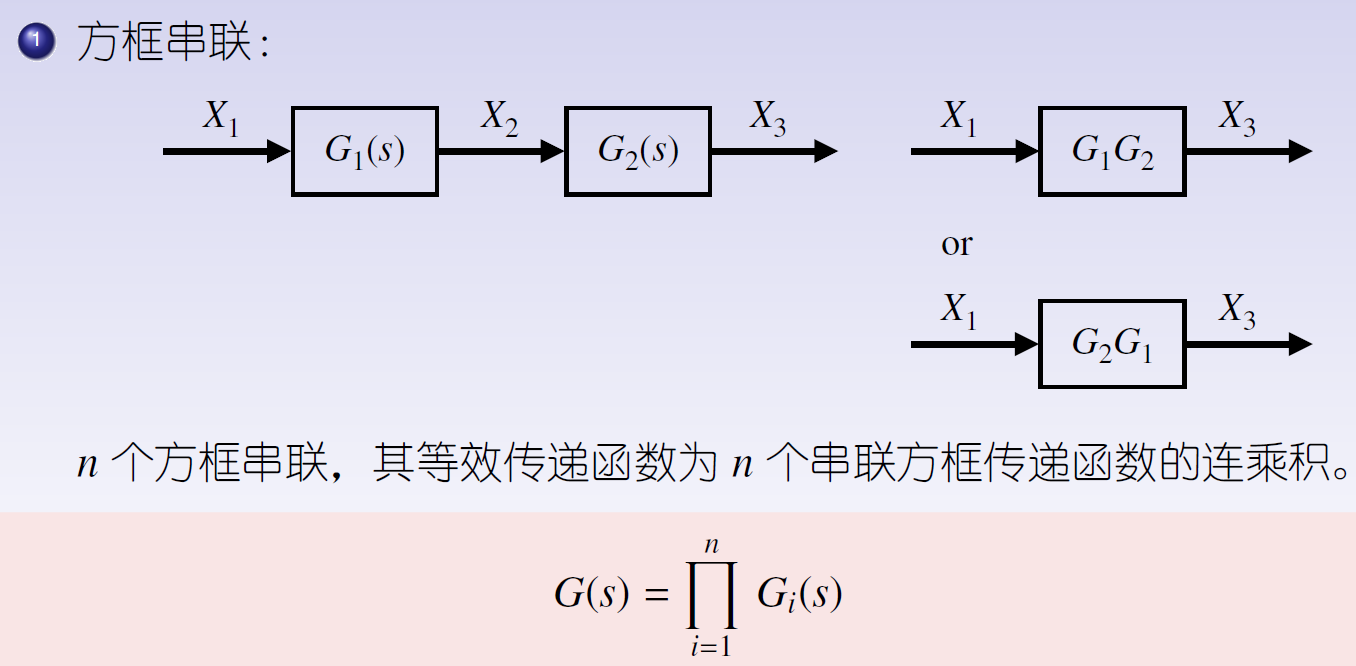
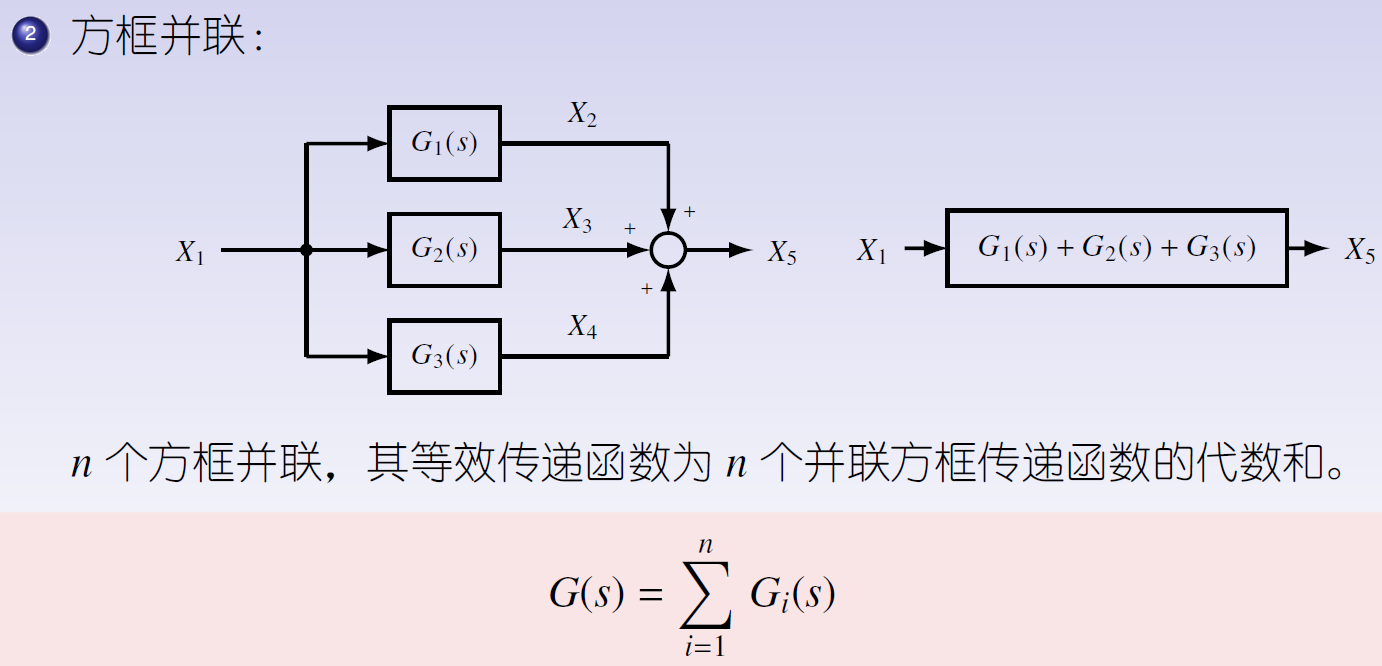
2.2.3.3 化简案例
例1
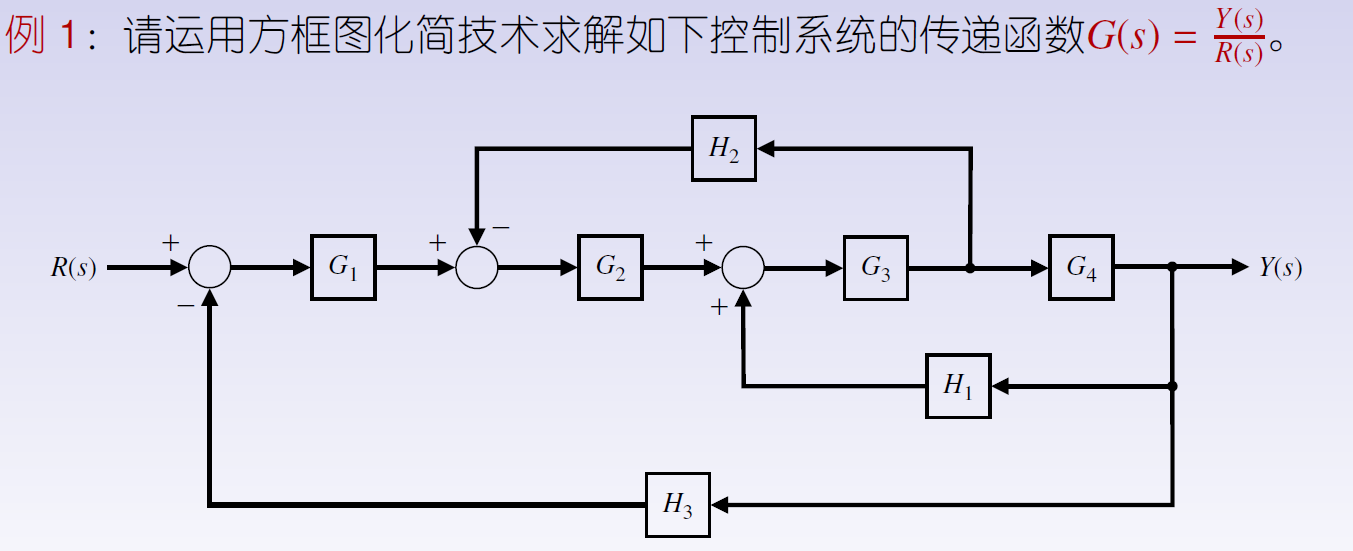
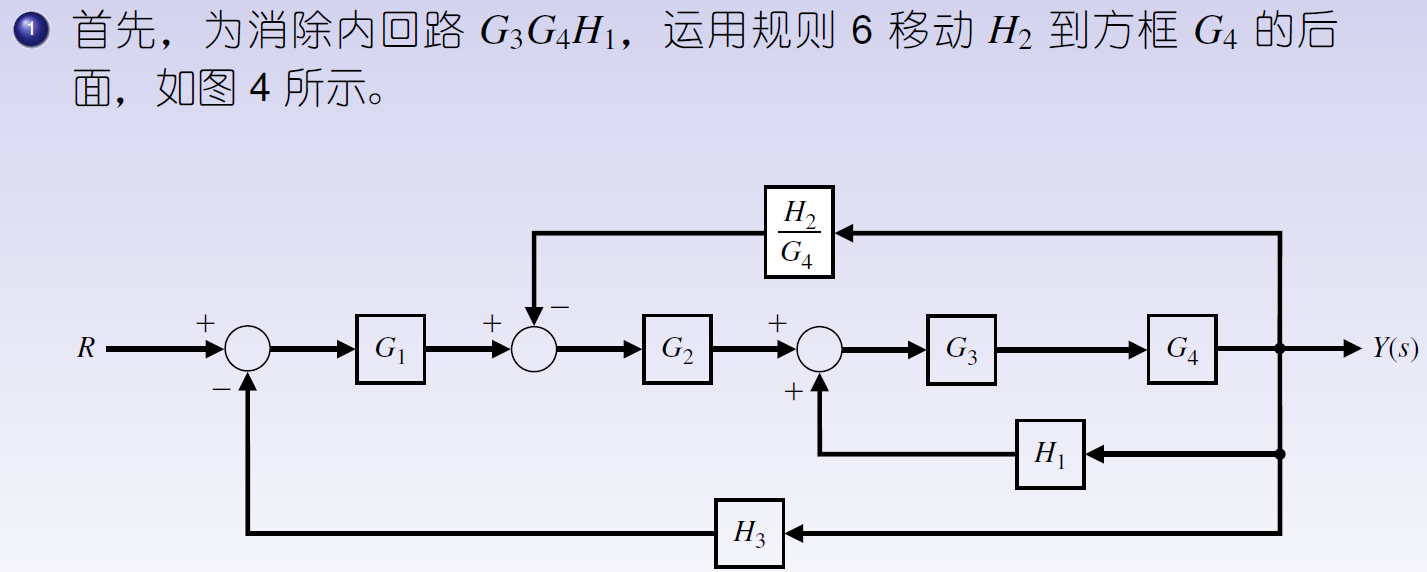
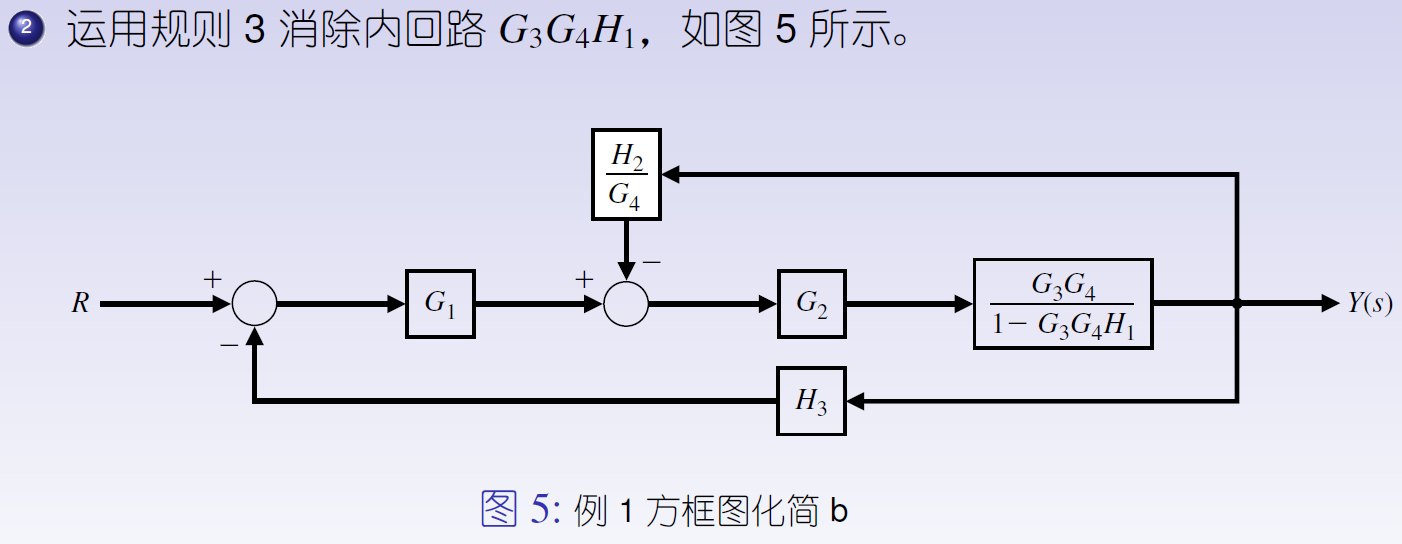
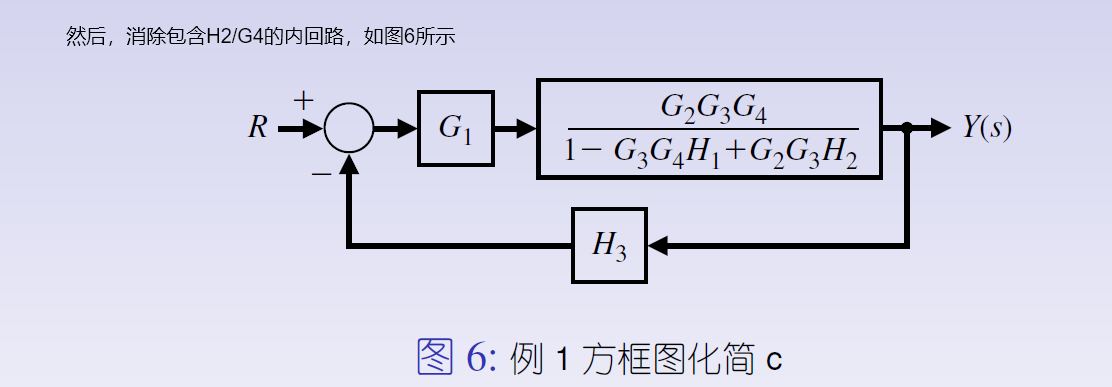
最后,消除含有H3的回路,如图7所示

例2
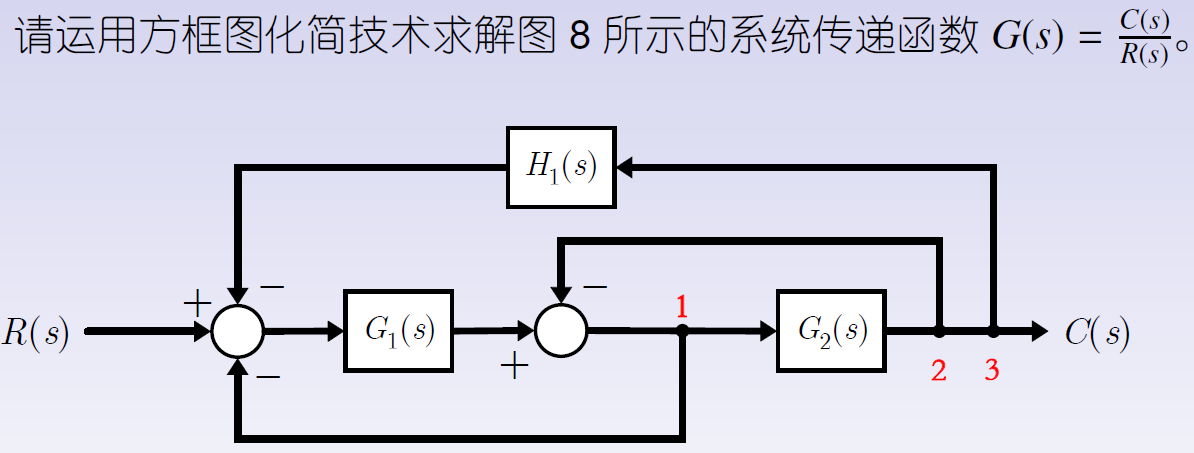
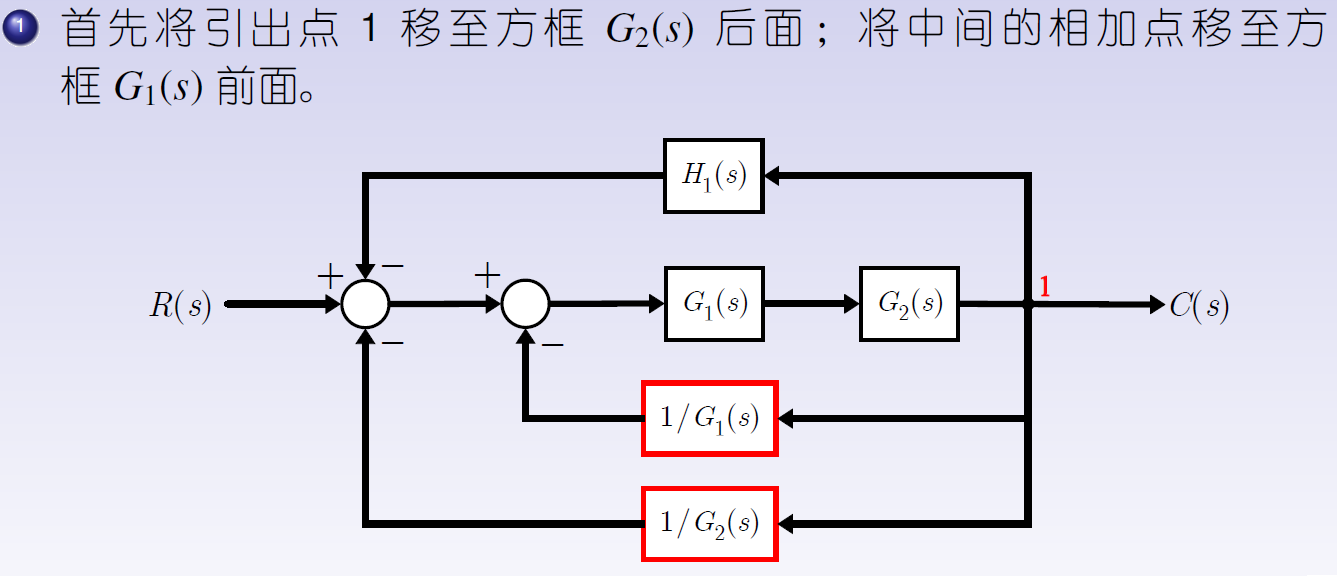
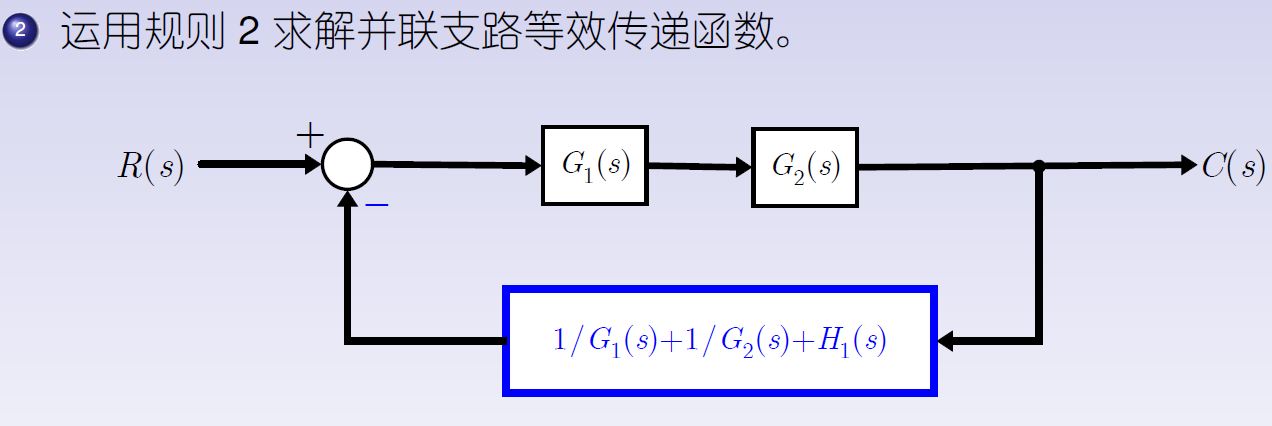
最后,运用规则3消除反馈回路获得传递函数
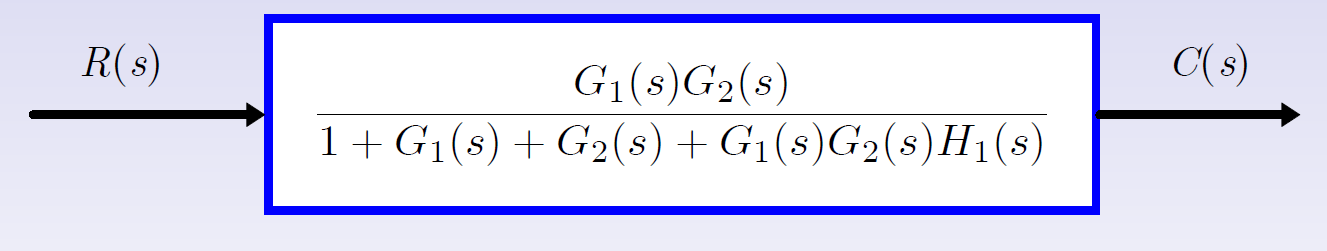
例3
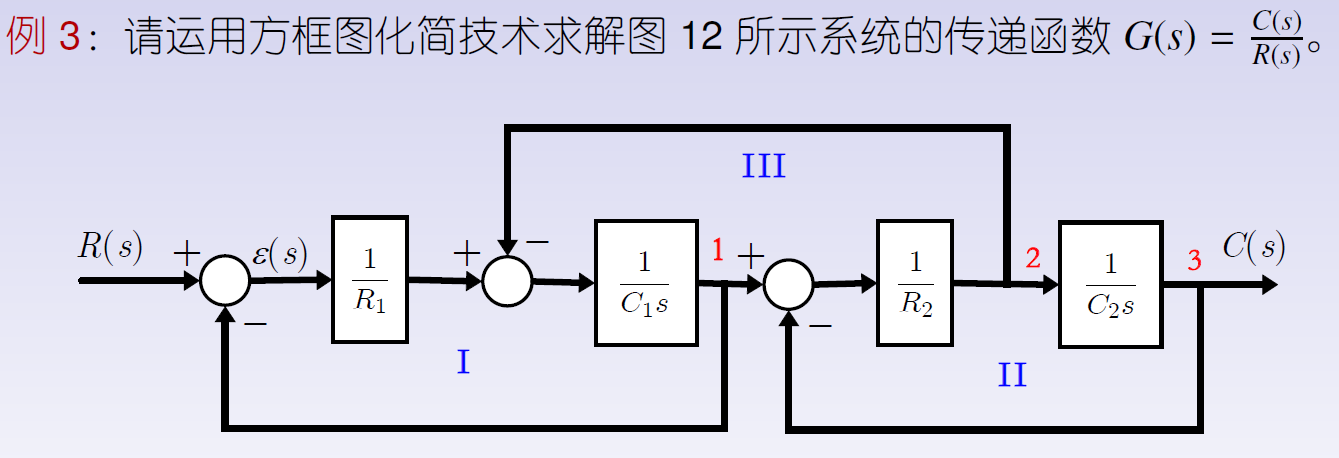
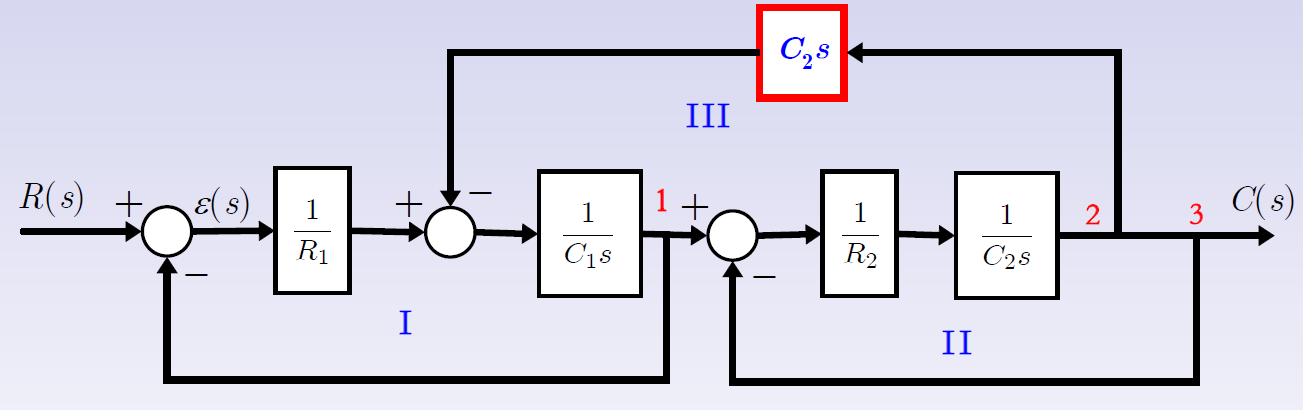
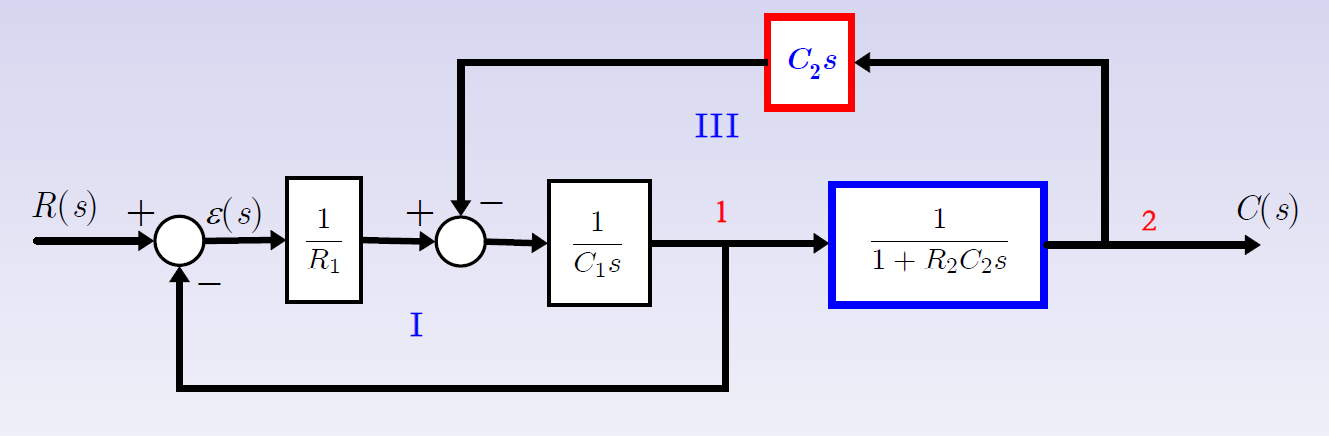
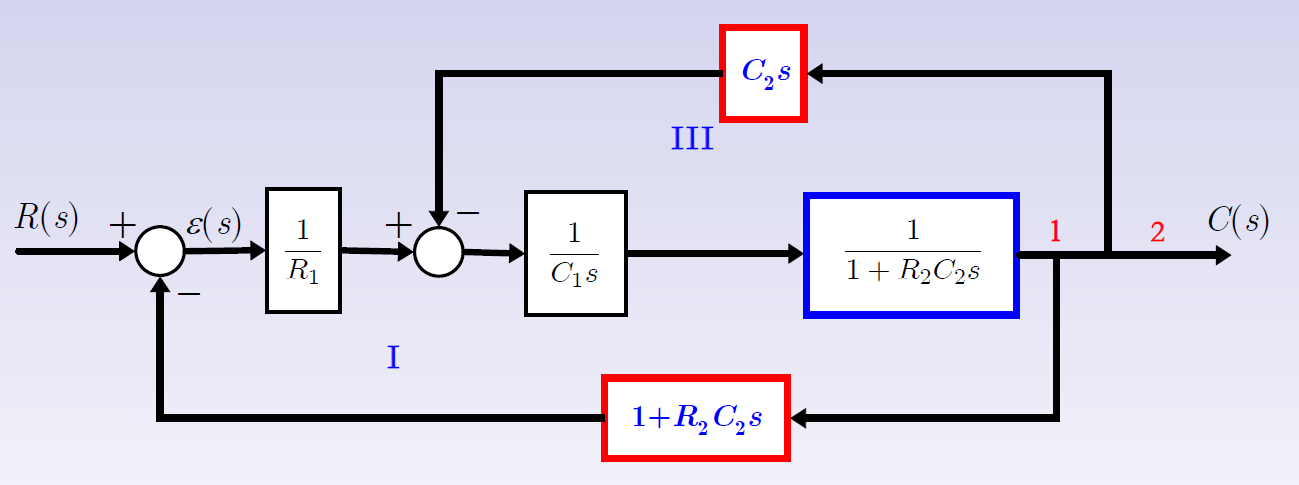
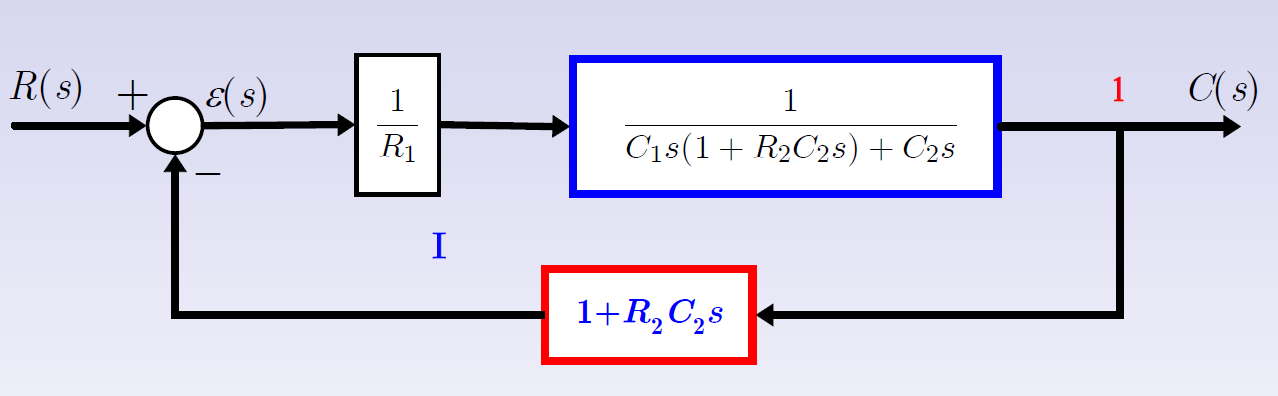
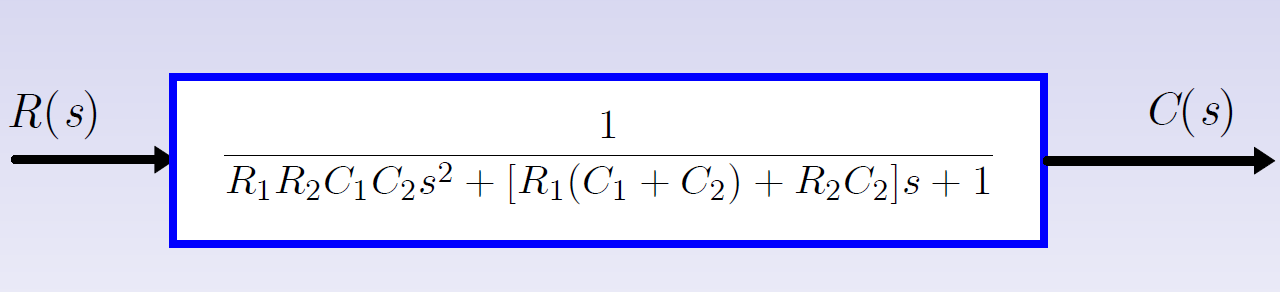
2.3 信号流图
2.3.1 概念
信号流图是由节点以及连接节点的支路构成的,是一组线性关系的图解表示。
- 信号流图由节点和支路构成
- 与方框图相比,信号流图更加简洁,便于绘制和应用
- 信号流图仅仅适用于线性系统,存在局限性;而方框图并无此局限。
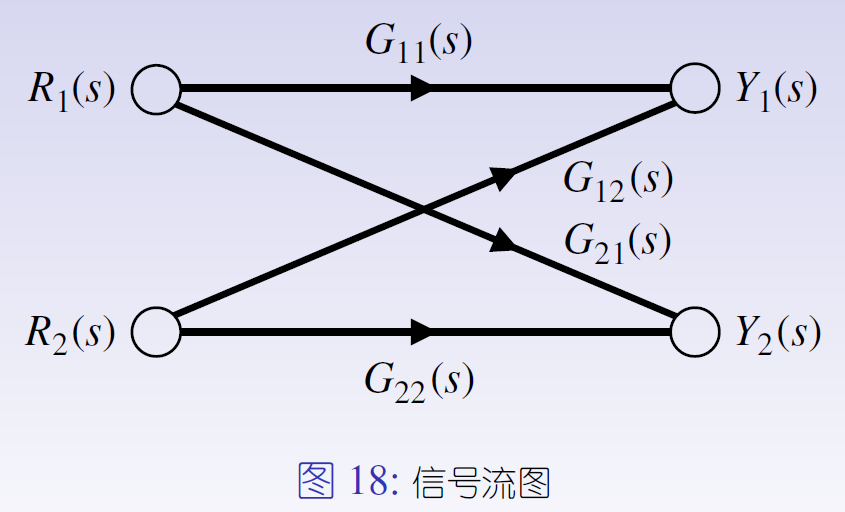
图18所示的信号流图表示的一组线性关系为:
- Y1(s) = G11(s)R1(s) + G12(s)R2(s)
- Y2(s) = G21(s)R1(s) + G22(s)R2(s)
2.3.2 名词解释
- 节点:用以表示变量或信号的点,称为节点。
- 节点可分为:输入节点(源节点)、输出节点(阱节点)和混合节点。
- 支路:联系两个节点,并标有信号流向和增益(传递函数)的定向线段,称为支路。
- 前向通路:开始于输入节点,沿支路箭头方向,每个节点最多只经过一次,最终到达输出节点的通路称之为前向通路。
- 前向通路上各支路增益之乘积,称为前向通路总增益。
- 回路:起点和终点在同一节点,除起点(或终点)外,与其他节点最多只经过一次的闭合通路,称为回路。
- 回路中所有支路的乘积称为回路增益。
- 不接触回路:回路之间没有公共节点时,这些回路叫做不接触回路。
- 自回路:只含有一个节点的回路,叫做自回路。
2.3.3 信号流图说明
- 信号流图仅适用于线性系统。
- 支路表示一个信号对另一个信号的函数关系,相当于乘法因子。信号只能沿支路上的箭头指向传递。
- 在节点上可以把所有输入支路的信号叠加,并把相加后的信号送到所有的输出支路。
- 对于混合节点,通过增加一个具有单位增益的支路把它作为输出节点来处理。
- 对于一个给定的系统,信号流图不是唯一的。
2.3.4 方框图变换为信号流图
2.3.4.1 具体步骤
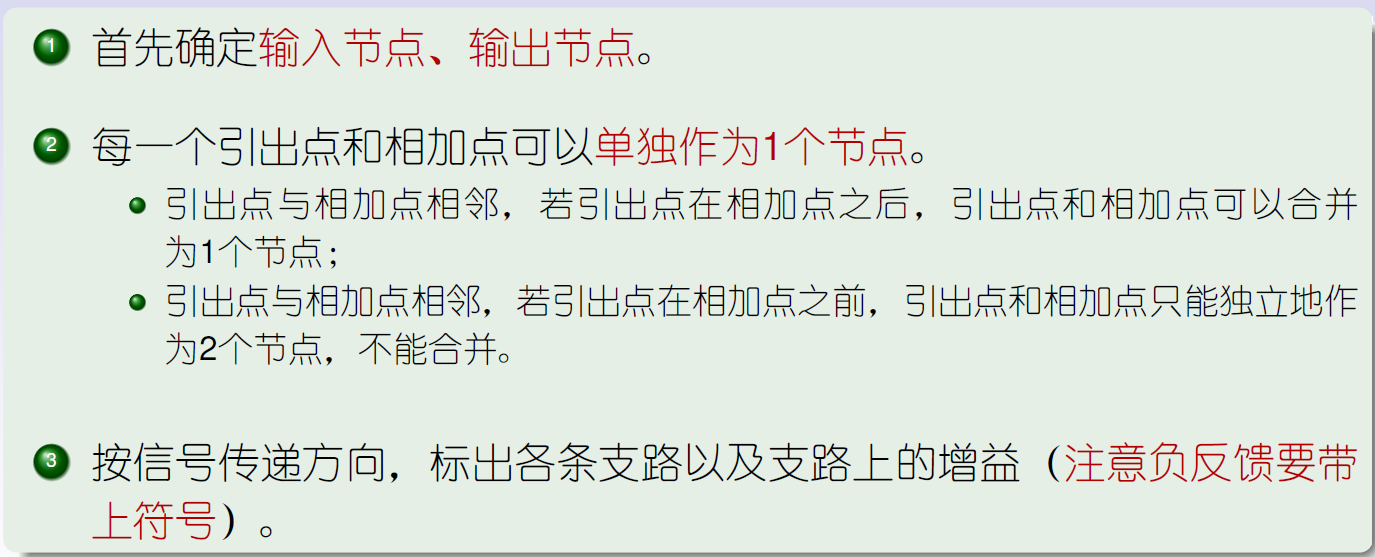
2.3.4.2 例
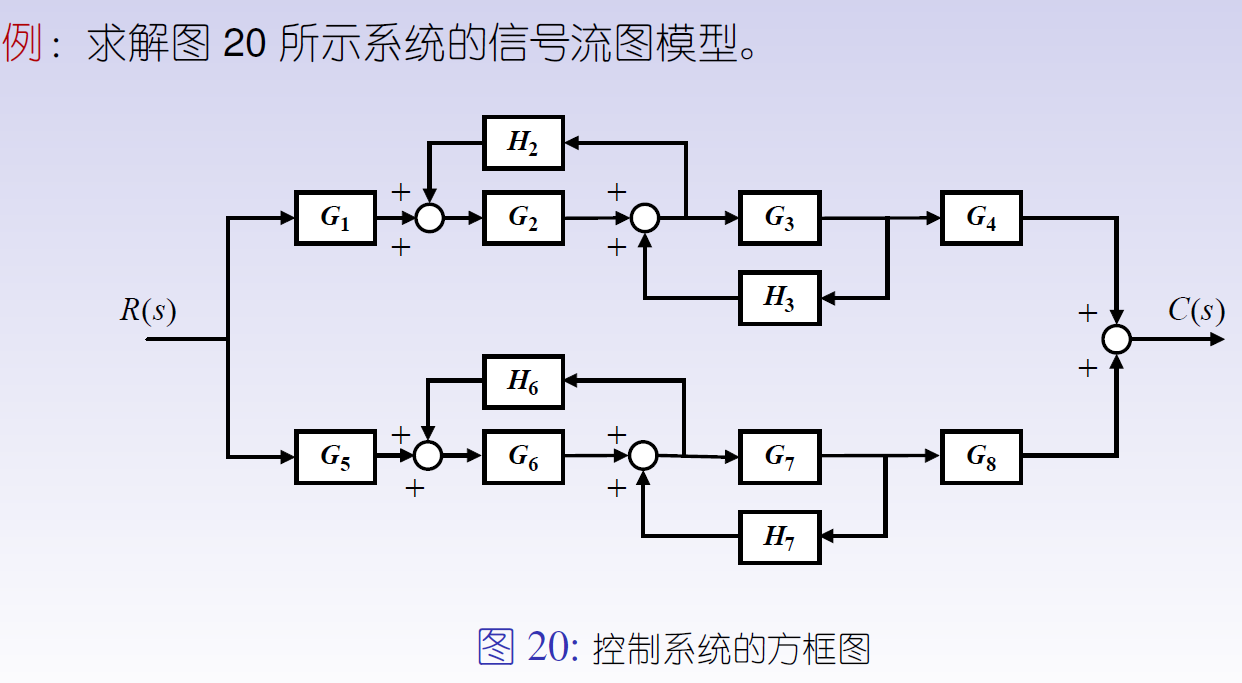
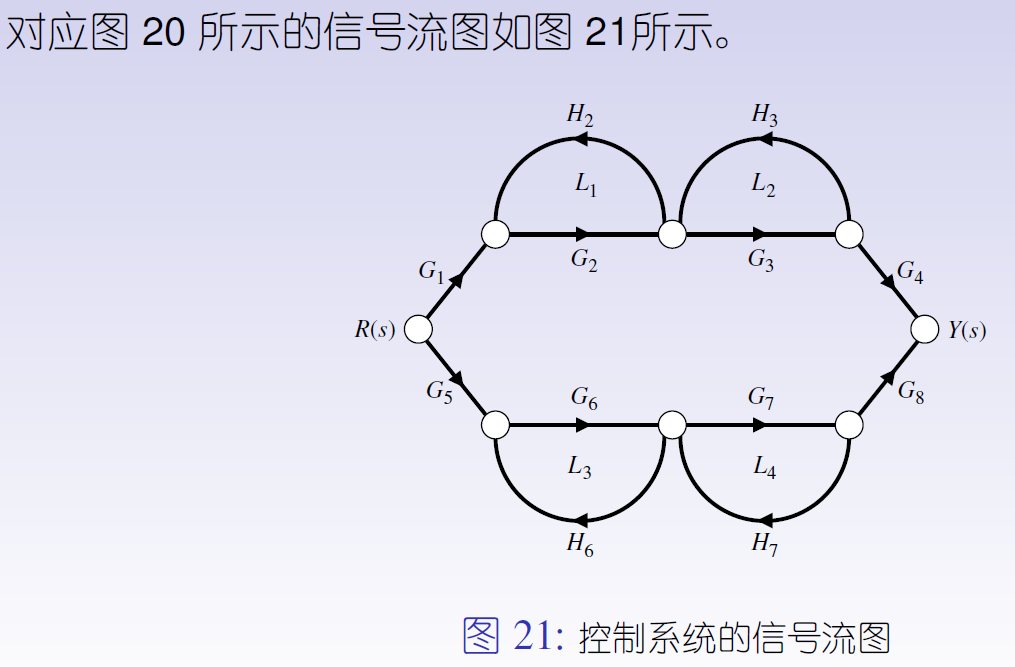
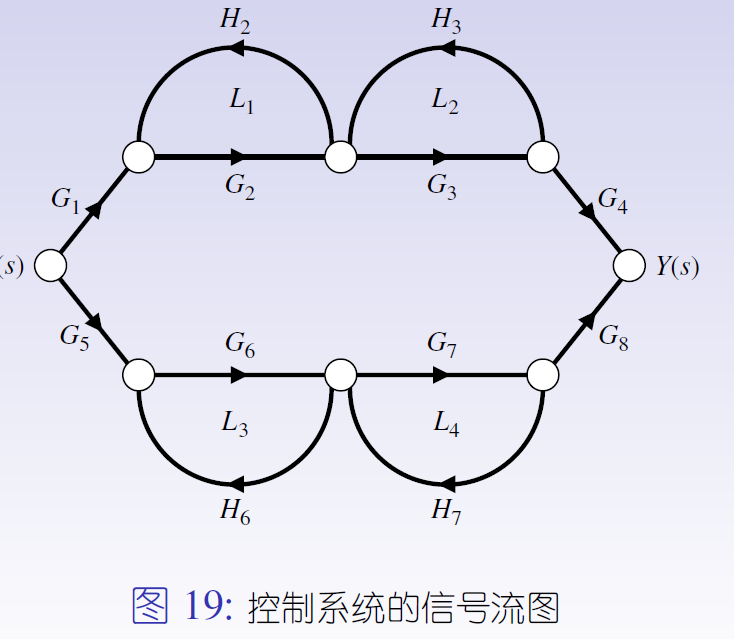
2.3.5 梅森增益公式
2.3.5.1 概念


2.3.5.2 应用

例1
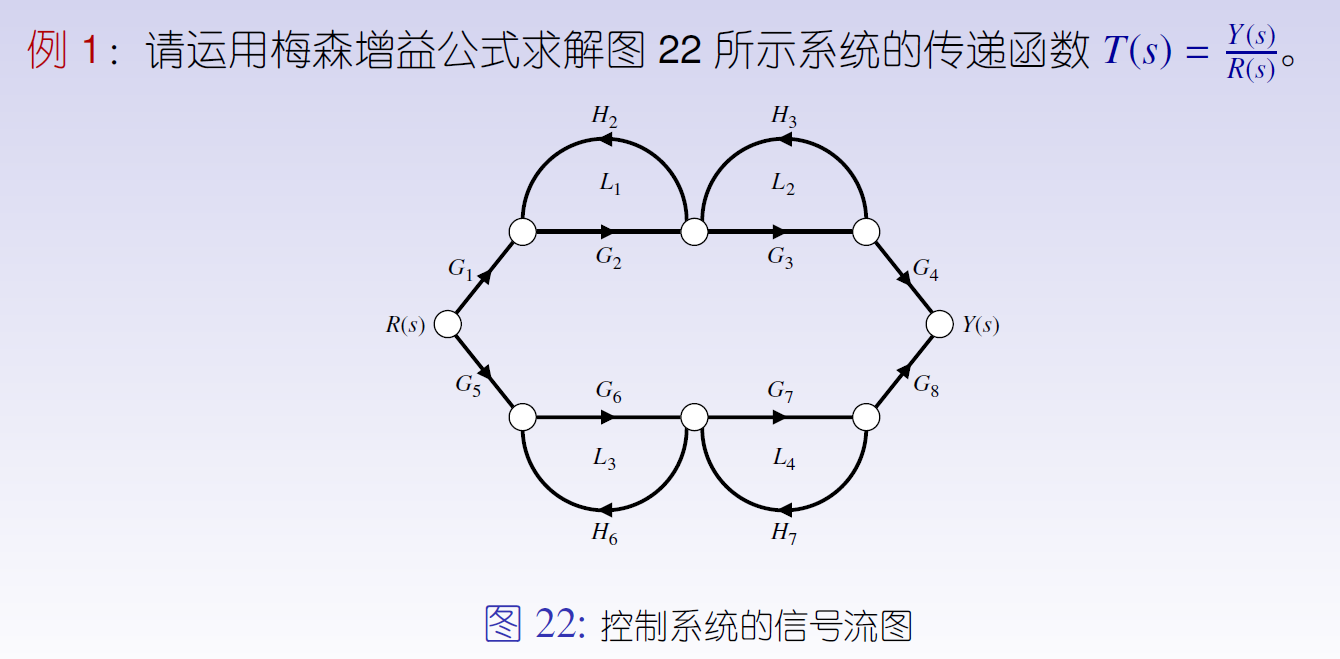
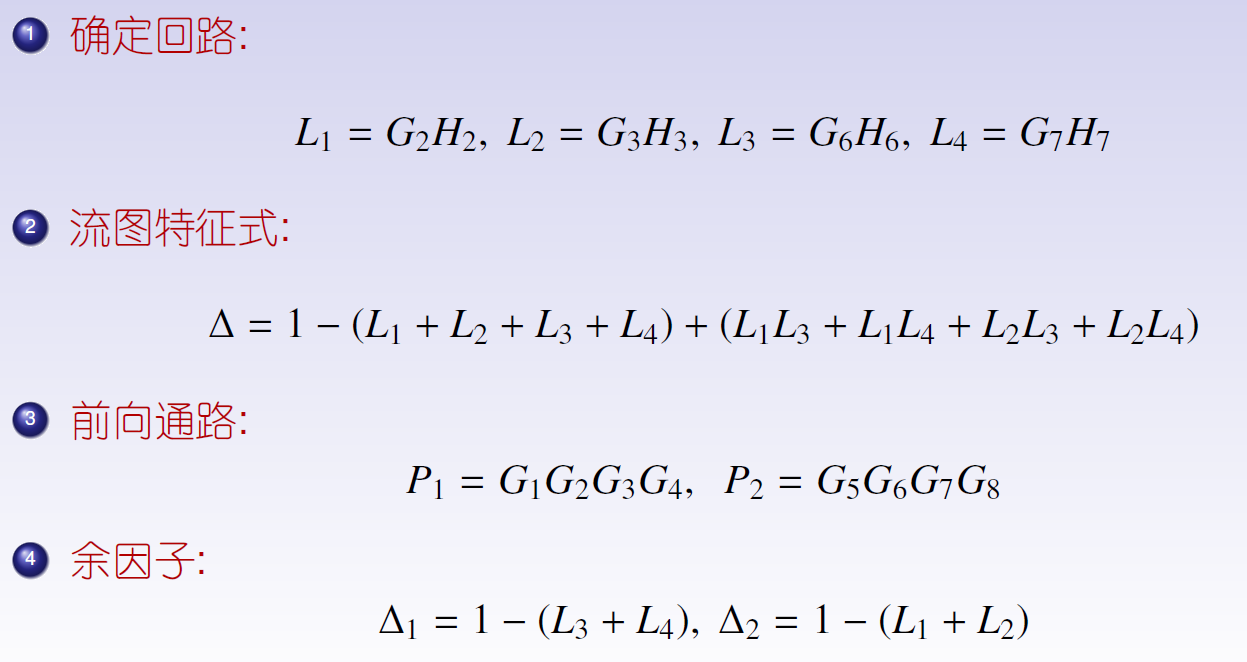
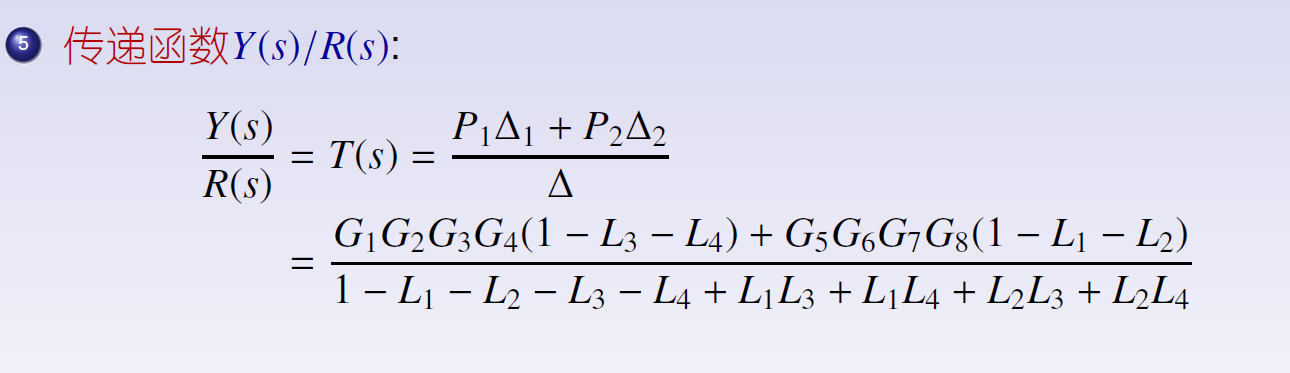
例2
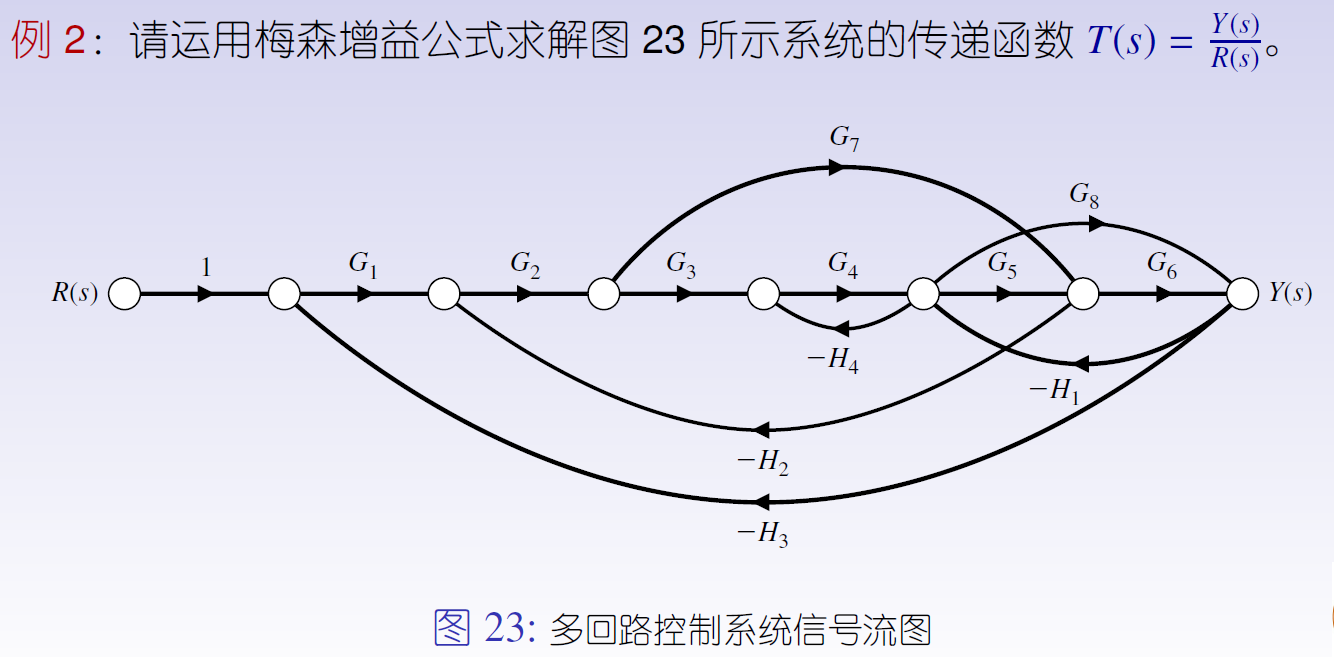
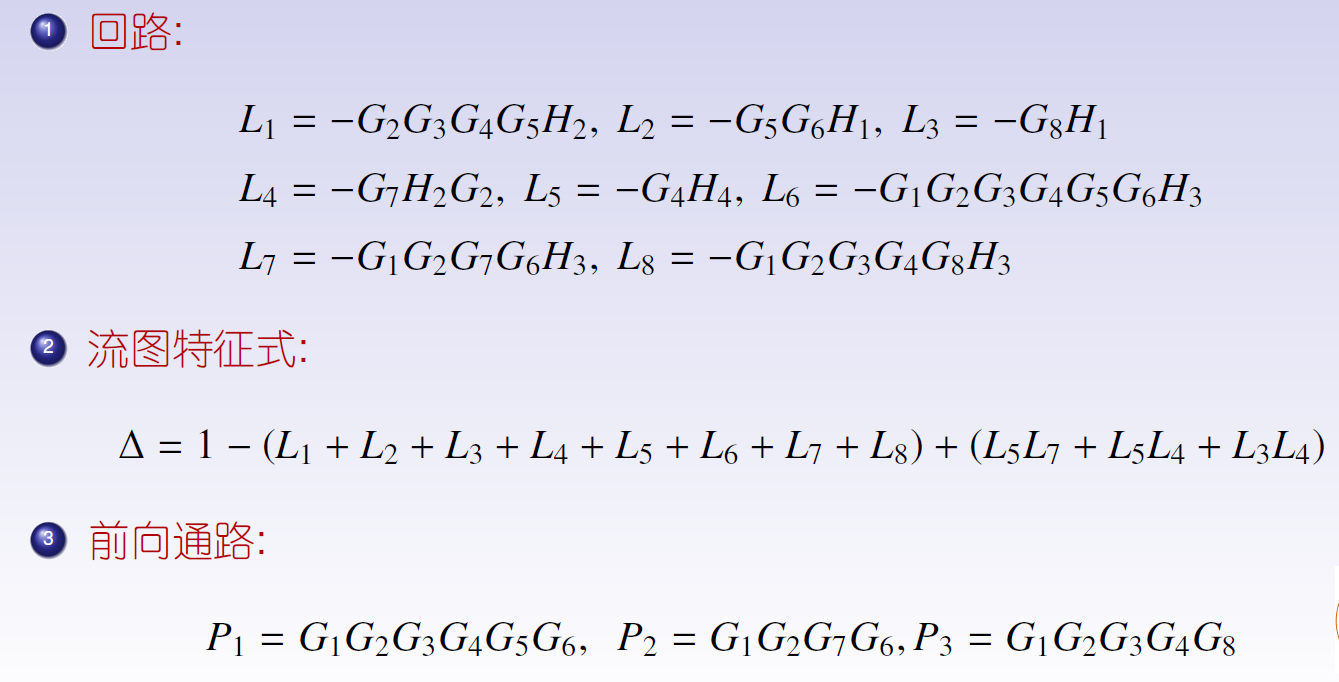
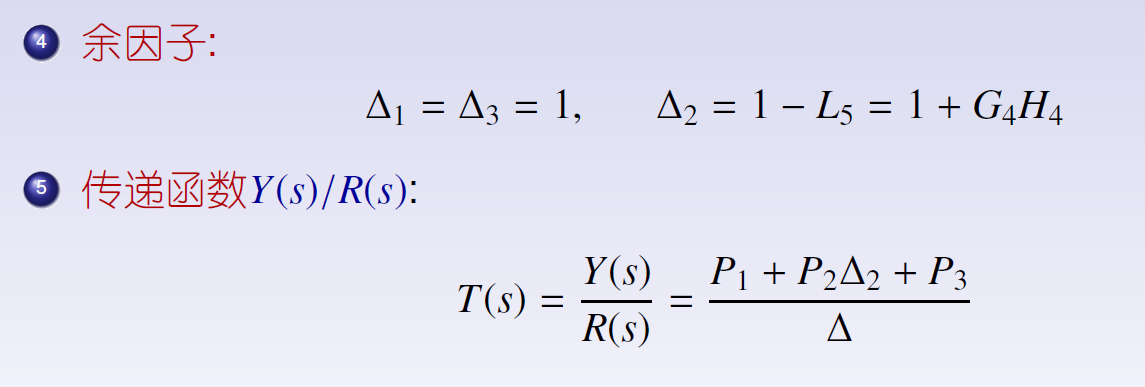
三、拉普拉斯变换
3.1 拉普拉斯变换定义
- 傅氏变换及拉氏变换意义(作用):
- (1)工程实践中求解微分方程的工具;
- (2)建立系统复域频域模型的数学基础。
-
拉普拉斯变换定义
- 时间函数f(t),当t<0时,f(t)=0;当t≥0时,f(t)的拉普拉斯变换记为L[f(t)]或F(s),定义如下
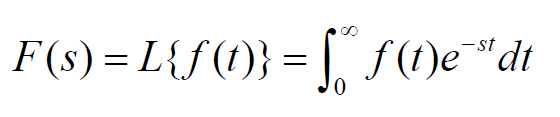
- 时间函数f(t),当t<0时,f(t)=0;当t≥0时,f(t)的拉普拉斯变换记为L[f(t)]或F(s),定义如下
-
拉普拉斯变换解读

3.2 拉普拉斯变换性质
- (1)线性性:
- (2)微分定理:
- (3)积分定理:
- (4)初值定理:若函数f(t)及其一阶导数都是可拉氏变换的,则函数f(t)的初值为
- (5)终值定理:
- (6)位移定理:
- (7)相似定理:
- (8)卷积定理:
3.3 拉普拉斯反变换
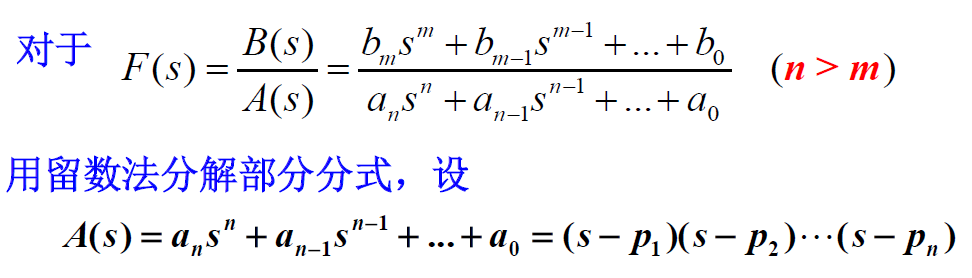
(1)当A(s)=0无重根时:
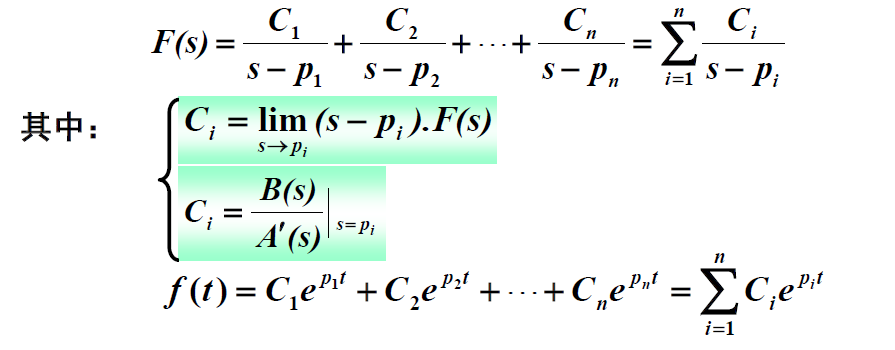

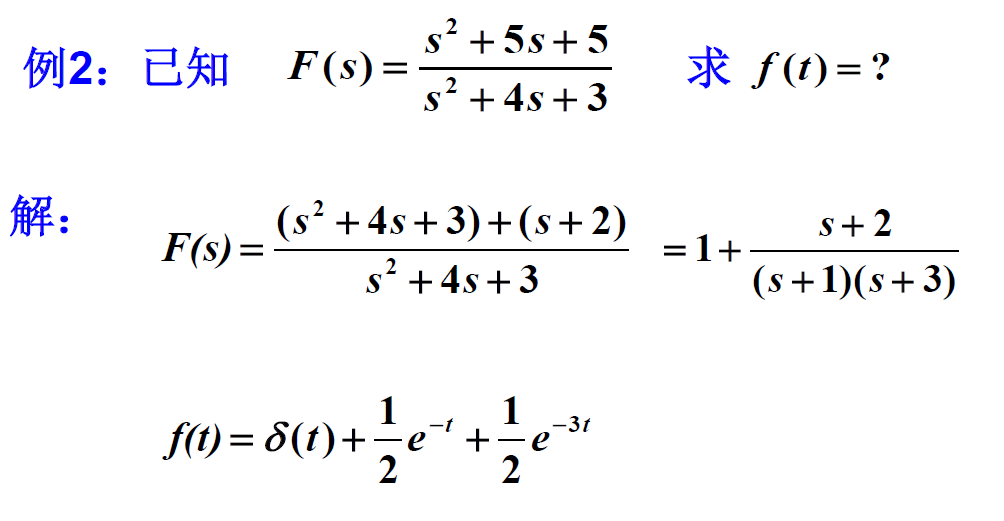

(2)当A(s)=0有重根时:

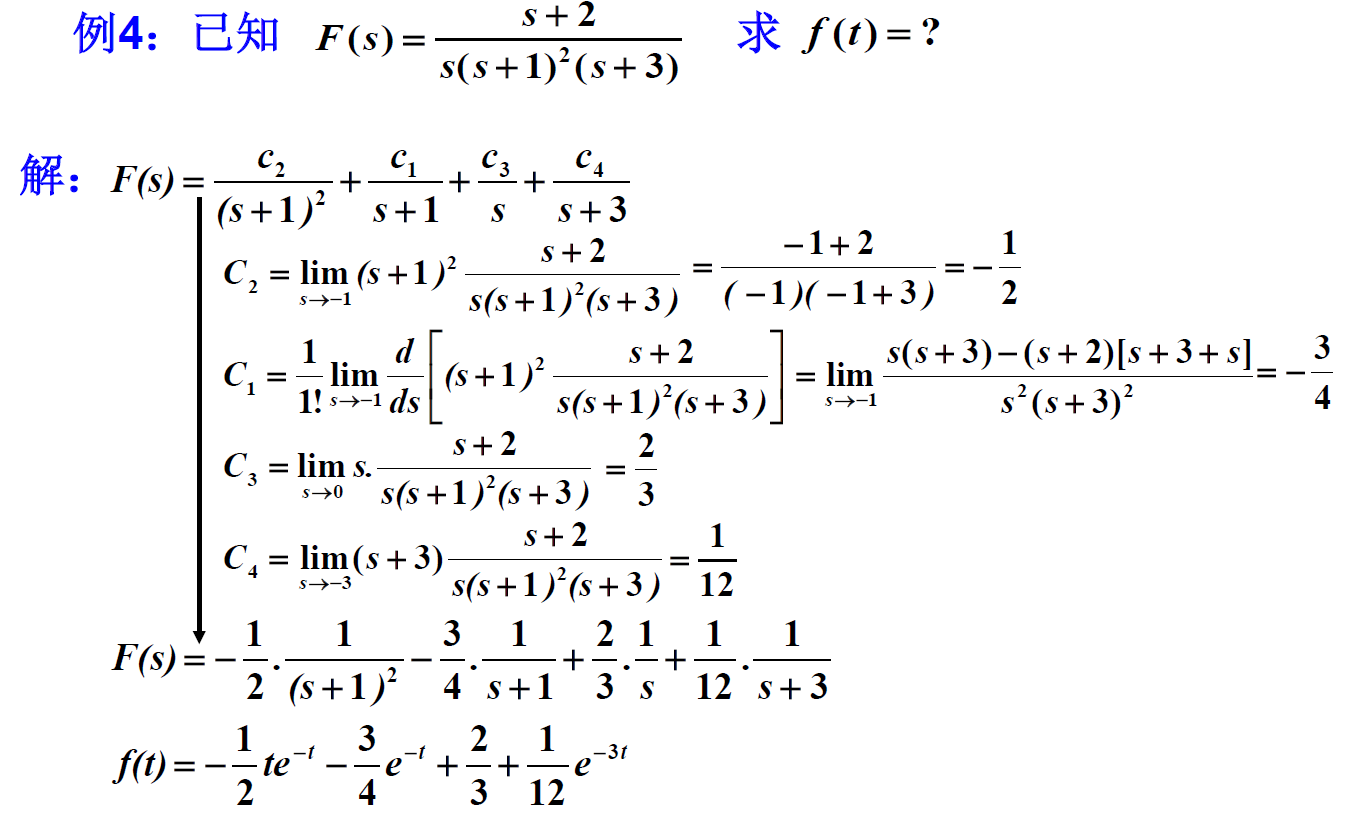






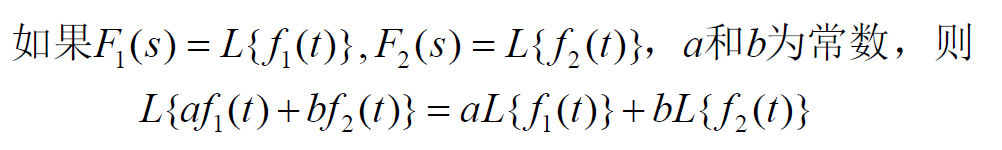
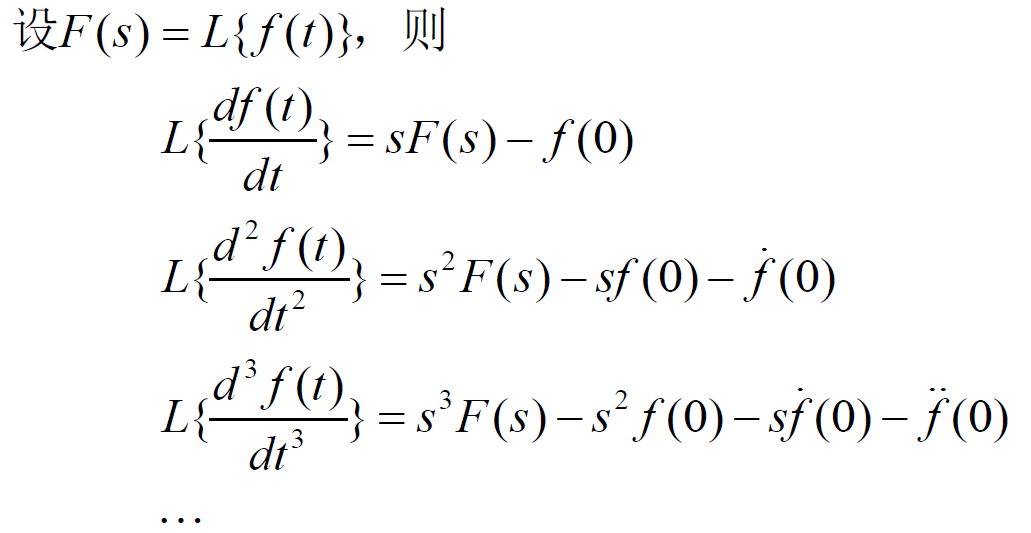
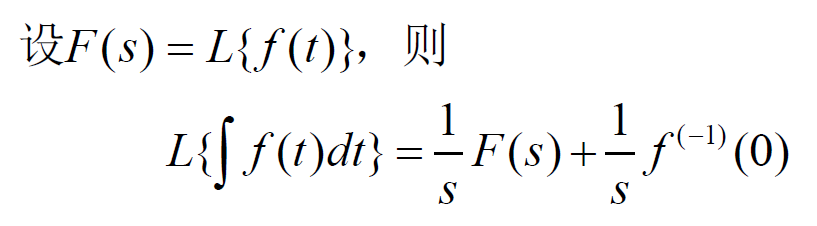
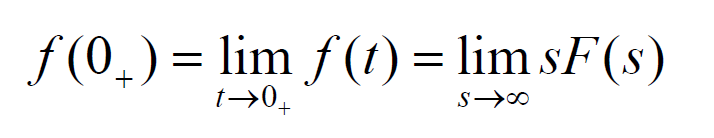

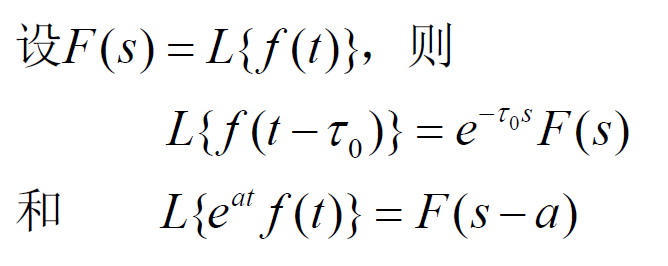
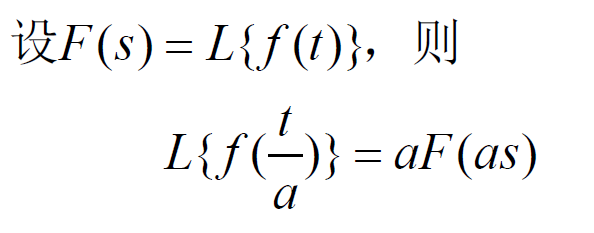
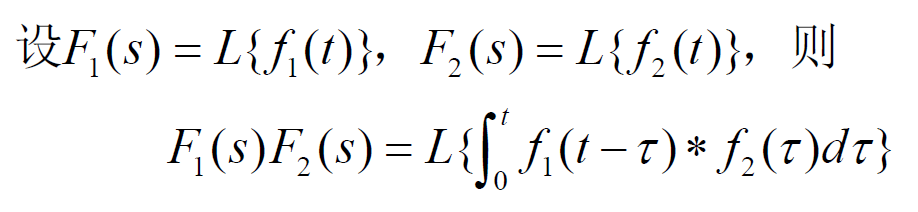
















 905
905

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








