《微波技术基础》第二版 阅读随笔2

第三章 分布电路与传输线理论

3.1 微波传输线

前面已经提到微波的波长单位在毫米到米之间，微波传输线由于线长与工作波长在同一数量级，因而被常称为长线。在这个频段，信号在传输线上所产生得到趋肤效应，导线之间的串扰以及漏电流等寄生参数所造成的影响不可忽略。即微波传输线本身就可以用一个集总参数电路来表示。这里我们所讨论的传输线除了起点和终点，其他位置上的电压和电流相位一致。
电磁能量的传输有两种方式：一是由传输线导体中的电流所携带；二是由传输线导体周围的媒质进行传播。

3.1.1 微波传输线的定义

微波传输线用于传递能量和信息，对传输线的基本要求有：

1. 传输损耗要小，传输效率要高。
2. 工作频带要宽，以增加信道容量，保证信号无畸变传输。
3. 在大功率系统中，要去传输功率容量要大。

3.1.2 分类

在微波频段，由于导线的趋肤效应和辐射效应增大，低频传输线无法直接应用在微波频段。PCB中通常由表层或内层的信号传输线构成微带线或带状线，它们都属于TEM波传输线，TEM波是指电矢量和磁矢量都与传播方向垂直的电磁波。
介质表面的导线是微带线（PCB表层线路）。
被介质包围的导线是带状线（PCB内层信号线）。

3.2 长线理论与分布参数

3.2.1 电路理论与传输线理论的区别

电路理论与传输线理论的关键差别是电尺寸。通常在集总参数电路分析中，因为元器件尺寸比信号波长小得多，因而可以不考虑电路各处电流、电压的幅值和相位的变化。但在传输线理论中，传输线的长度与工作波长在同一数量级，传输线上的电压电流的幅值和相位不再仅是时间的函数，还与位置有关。另外由于传输线介质的物理性质所造成的趋肤效应、导线之间的串扰、辐射、漏电流使得分布参数的影响不可忽略。

3.2.2 分布参数效应

当高频信号通过传输线时，会产生下列分布参数：

1. 导线流过电流时，周围会产生高频磁场，因而沿导线各点会存在串联分布电感。
2. 两导线之间加上电压时，线间会存在高频电场，于是线间会产生分布电容。
3. 导电率优先的导线流过电流时会发热，而且高频时由于趋肤效应，电阻会加大，集表明线本身有分布电阻。
4. 导线间介质非理想时有漏电流，这意味着到仙剑有分布电导（导纳S）
   以上这些因素在低频时影响较小，可以忽略；而在高频时引起的沿线电压、电流幅度变化、相位滞后时不能忽略的，这就是所谓的分布参数效应。
   补充：趋肤效应的应用
   使用空心导线以节约原材料。
   使用多股相互绝缘的细导线编制成束代替具有同样截面积粗导线，这种多股线称为辫线。
   利用趋肤效应可以对金属表面进行淬火。

3.2.3 长线理论

所谓长线是相对于工作频率而言的。这里我们定义一个概念：电长度，$l/\lambda$。其中$l$是线长，$\lambda$是信号波长。通常认为线长满足 $l/\lambda >0.1$，也就是线长大于波长的10倍。在短线上可以认为信号电流或电压是处处相同的，此时，电压和电流仅仅是时间的函数，与位置无关。但在长线上，时间和位置共同作为信号幅值和相位函数自变量。

3.2.4 分布参数

传输线的主要分布参数可以具体为：

1. 由于传输线导体非理想而产生的分布电阻R。
2. 由于两条靠近的传输线之间的介质非理想而产生的分布电导G。
3. 传输线自感产生的分布电感L。
4. 两导线之间存在压降而构成分布电容C。
   以上4个分布参数可以用下面的等效电路来表示：

3.3 传输线的等效电路

对照上图可以明确，传输线的分布参数可以用分布电阻$R_0$、分布电感$L_0$、分布电容$C_0$、分布电导$G_0$来描述。这些参数是由传输线形式、尺寸、导体材料、介质参数共同决定的。根据传输线的分布参数是否均匀不变，传输线可以分为均匀传输线与非均匀传输线。对于均匀传输线如果可以满足波长范围内，传输线性质变化非常小，即$dz<<\lambda$,那么可以认为传输线构成了一个集总参数电路。

3.4 传输线方程及其求解

3.4.1 什么是传输线方程

使用基尔霍夫电压定律和基尔霍夫电流定律对上图中的传输线模型进行描述可以得到：

公式1

$$\{\begin{array}{r}输入端电压-分布电阻R_0分压-分布电感L_0分压-输出端电压=0\\ 输入端电流-分布电导G_0分流-分布电容C_0分流-输出端电流=0\end{array}$$
由微分的定义可知，当截取的一段导线足够小时，导线输入和输出端的电压、电流可以用下面的微分形式表示。
与公式1联立得到

公式2
式中描述了电压$v(z,t)$和电流$i(z,t)$随传输距离$z$的衰减速度分别与分布参数之间的关系。微分方程组公式2就是所谓的传输线方程。
对于$v,i$随时间简谐变化的波（正弦波）：
$$\{\begin{array}{r}v(z,t)=Re[V(z)e^{j\omega t}]\\ i(z,t)=Re[I(z)e^{j\omega t}]\end{array}$$带入到公式2中
$$\{\begin{array}{r}-\frac{\partial Re[V(z)e^{j\omega t}]}{\partial z}=R_{0}Re[I(z)e^{j\omega t}]+L_0\frac{\partial Re[I(z)e^{j\omega t}]}{\partial t}\\ -\frac{\partial Re[I(z)e^{j\omega t}]}{\partial z}=G_{0}Re[V(z)e^{j\omega t}]+C_0\frac{\partial Re[V(z)e^{j\omega t}]}{\partial t}\end{array}$$微分后等式两边约掉$e^{j\omega t}$和求实部运算$Re[]$得到$v，i$的复振幅方程，在第二章中我们说过相量$V,I$中所包含的信息中包含振幅信息和初始的相位信息，是一个复数，也就不难理解为什么叫复振幅方程。

公式3

令沿导线传播的阻抗$Z=(R_0+j\omega L_0)$和导线之间相互作用的导纳$Y=G_0+j\omega C_0$进一步改写公式3可以得到：

公式4

3.4.2 传输线方程的解

1.通解

对公式4两边再对$z$进行微分（原图不规范，遂将平方位置移动到微分符之后）

再将公式4带入上面的微分结果：$$\{\begin{array}{r}\frac{d^{2}V(z)}{d{z}^2}-ZYV(z)=0\\ \frac{d^{2}I(z)}{d{z}^2}-ZYI(z)=0\end{array}$$
令$\gamma =\sqrt{ZY}=\sqrt{(R_0+j\omega L_0)(G_0+j\omega C_0)}=\alpha +j\beta$，$\gamma$定义为传输线的传播常数，其中$\alpha$为衰减常数，$\beta$为相位常数。将传播常数带入方程组中
$$\{\begin{array}{r}\frac{d^{2}V(z)}{d{z}^2}-{\gamma }^{2}V(z)=0\\ \frac{d^{2}I(z)}{d{z}^2}-{\gamma }^{2}I(z)=0\end{array}$$求解微分方程可以得到通解的形式为:

由公式4可进一步将通解的形式统一为电压表示形式：传输线方程的最终简化形式为：

公式5 传输线方程通解的基本含义是：传输线上电流和电压入射波与反射波的叠加。

注意到我们用$1/Z_0$代替$\gamma /Z$，当传输线阻抗匹配时将不会存在反射，此时入射波电压与入射波电流之比（行波电压与行波电流之比）称为传输线的特征阻抗$Z_0$
回顾传播常数的定义：$\gamma =\sqrt{ZY}=\sqrt{(R_0+j\omega L_0)(G_0+j\omega C_0)}$，传播常数是传输线的阻抗和传输线之间的导纳相乘并开平方的结果。不难发现因为阻抗和导纳互为倒数的关系，传播常数的单位是$1$而特征阻抗的单位恰好是$\Omega$。

低损耗传输线

大多数微波传输线的损耗非常小，可以做出一些近似来简化运算。

公式6

如果线是低损耗的，我们认为传输线材质的分布电阻$R_0$很小，因为传输线介质导致的漏电流很小，即分布电导（导纳），$G_0$很小。相对于分布电容和分布电感来说有如下关系：

$$R_0\ll \omega L_0；G_0\ll \omega C_0$$

所以公式6中最末项$\frac{R_0{G}_0}{{\omega }^2{L}_0{C}_0}\to 0$，所以有：

这里我们使用泰勒级数展开$\sqrt{1-x}=1+x/2$，仅保留前两项得到：

公式7

由此我们得到衰减常数$\alpha$和相位常数$\beta$可以分别表示为：

无损耗传输线

无损耗传输线是一种理想模型满足$R_0=0;G_0=0$，由公式7我们可以得到无耗传输线的传播常数$$\gamma =j\omega \sqrt{L_0{C}_0}=j\beta$$
进一步我们可以得到无耗传输线上，传输线方程得到通解为：

由边界条件确定传输线方程特解

由边界条件$z=0时，V(0)=V_L;I(0)=I_L$带入公式5可以得到：
进一步我们可以得到在$z=-l$处电压以及电流的分布表达式为：

利用双曲线表达式$chx=\frac{e^x+e^{-x}}{2},shx=\frac{e^x-e^{-x}}{2}$则上式可简化为：

公式8 补充： 双曲正弦sh

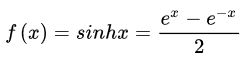
双曲余弦ch

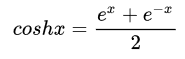
双曲正切th

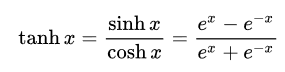
3.5 传输线的特征参数

3.5.1 输入阻抗

输入阻抗用来描述传输线上由反射波和入射波叠加组成的合成波的阻抗特性。传输线上任意一点的输入阻抗$Z_{in}$定义为该点的合成波电压与合成波电流之比。即：括号内的z为传输线上一维空间坐标，传输线上的任意一点都有自己对应的输入阻抗。当传输线距离负载为$l$时输入阻抗可以将公式8的结果带入上式，得到式中$Z_L$为终端负载阻抗，$Z_L=\frac{V_L}{I_L}$。上面已经讨论过，对于无耗传输线，$\gamma =j\omega \sqrt{L_0{C}_0}=j\beta$，衰减常数$\alpha =0$，$\gamma =j\beta$，另外推算得到$th(j\beta l)=th(\beta l)=jtan(\beta l)$。所以均匀无耗传输线上距离负载$l$处的输入阻抗为：

公式9

可以看到，输入阻抗只与传输线的特征阻抗$Z_0$负载阻抗$Z_L$以及观察点与负载之间的距离$l$有关。
补充：低耗传输线与无耗传输线的相位常数$\beta$相同，$\beta =\omega \sqrt{L_0{C}_0}$。
传输线上任意一点的输入阻抗相当于由该点向负载看去所呈现的阻抗。换句话说，它时负载经一段长为$l$的传输线变换后在该点的反应阻抗。因此，在传输线上某一点，其右端的一段传输线及负载的作用，可以用在该点借一个其值等于该处输入阻抗$Z_{in}$的集总参数阻抗来等效。如下图所示:

通过公式9可以看出当$Z_L=Z_0$时$Z_{in}=Z_0$即，当传输线的特征阻抗（$Z_0=\sqrt{\frac{Z}{Y}}$）与负载阻抗阻抗$Z_L$相等时，也就是接收端阻抗匹配时，传输线上的点的输入阻抗都等于特征阻抗，此时传输线上不存在反射。相反，当$Z_L\ne Z_0$时$Z_{in}$是关于$l$的周期函数,周期为$\lambda /2$。因此对于一个固定的负载阻抗，只要改变连接它的传输线长度即可改变其输入端的输入阻抗$Z_{in}$

3.5.2 反射系数

3.5.2.1 传输线方程解的物理意义

上式是我们前面提到的传输线方程通解
在确定坐标轴正方向指向负载，将通解表示某一瞬间$t$在实轴的投影。线上的任意一点电压、电流均由入射波和反射波两部分组成。以电压为例：$$V_0^{+}{e}^{-az}cos(\omega t-\beta z)$$表示沿正方向，信号幅度逐渐衰减，相位逐渐滞后。这是电压入射波的行为模式，同理，$$V_0^{-}{e}^{az}cos(\omega t+\beta z)$$表示沿负方向电压幅值指数衰减，相位逐渐滞后，这是电压反射波的行为模式，称为电压反射波。
因此，线上任意一点的电压和电流都有入射波和反射波的叠加，用数学语言表达为：
不难发现，当传输线的特征阻抗为实数时（容性和感性成分相互抵消），电压入射波与电流入射波的相位相同而电压反射波与电流反射波的相位相反。

3.5.2.2 反射系数

电压反射系数：传输线上任意一点的电压反射系数为该点电压反射波与电压入射波的幅值之比。

公式10

同理，电流反射系数的定义如下：

如前文所述，由于电流反射波与电压反射波的相位相反，所以电流反射系数与电压反射系数等大反向（相位相反）。通常，我们使用电压反射系数来表征反射特性。
在终端为无源负载时，通常$0\le |\tau (z)|\le 1$。

利用前面无耗传输线模型中利用边界条件求解的传输线方程特解：
将负载端特解带入公式10得到负载端反射系数如下图所示。
用$\varphi$来表示相位关系则有：

记得我们前面讨论过，在已知终端电压和终端电流时，传输线上在距离负载$z=-l$处电压及电流分布的表达式为：
同样，我们将上式中电压入射波和反射波分离出来带入公式10，得到更普适的表达，即传输线上$z=-l$的任一点反射系数如下图所示：

我们用$\varphi$来表示$\tau$中所包含的相位关系,进一步得到：
现在，我们根据电压入射波的初始值$V_0^{+}$和反射系数，可以得到在均匀无耗传输线$z=-l$处的电压表达式：
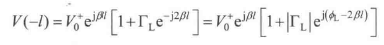在均匀无耗传输线上，各点的反射系数相同，在$z=-l$处，相位滞后于终端$2\beta l$
令$\phi ={\varphi }_L-2\beta l$，l为从负载到观察点的距离，则有：

---

上图中，理想均匀传输线上的总电压和总电流可以表述如下

3.5.3 驻波比

我们很难对入射波电压和反射波电压进行直接测量（电流也是如此），我们在传输线上进行测量直接得到的是入射波和反射波合成的驻波。我们引入驻波比$\rho$来描述传输线上的反射情况。
所谓驻波比就是传输线上电压振幅的最大值与最小值之比。
$$\rho =\frac{|V{|}_{max}}{|V{|}_{min}}$$。因为在传输线上任意任意一点的电压都是由入射波电压与反射波电压叠加而成的，所以当入射波电压与反射波电压同相位时电压出现最大值，反相位时，电压出现最小值：
注意：并不是波峰与波谷之间幅值的比，同相位比较才有意义。
因此，驻波比也可以表述为：
反过来反射系数用驻波比来表示为：
与驻波比概念类似，概念行波系数表示为：

3.5.4 输入阻抗与反射系数的关系

注意到，电流反射系数与电压反射系数等大反相，所以分母上是相减。反射系数与传输线本身的特征阻抗$Z_0$和输入阻抗$Z_{in}$有关。

3.5.5 传输功率

传输功率等于入射功率减去反射功率，对于正弦信号而言，入射和反射功率分别有如下表示形式：

3.6 传输线的工作状态

传输线的工作状态是指传输线上电流和电压的分布状态，传输线根据负载阻抗不同，有三种不同的工作状态，即行波、驻波、行驻波。

3.6.1 行波状态

行波状态下，传输线上无反射波，终端反射系数${\tau }_L=0$，传输线上各点的反射系数$\tau (z)=0$也均为0。
根据反射系数公式可以知道，此时传输线的负载阻抗与传输线的特征阻抗相等$$Z_0=Z_L$$此时的状态也被称为终端匹配。此时驻波比$\rho =1$

结合前面的讨论结果我们知道：

行波状态下传输线上任意一点的输入阻抗等于负载阻抗，与位置无关。
对于行波状态下的信号传输，电压和电流的表达式为:

行波状态下，传输线可以进行最有效的功率传输。

3.6.2 驻波状态

此时反射系数$|{\tau }_L|=1$
根据公式我们可以清楚的知道，全反射有两个状态可以满足：

1. 终端短路，$Z_L=0，{\tau }_L=-1$，此时传输线上的电压电流信号满足：
   在终端短路$z=0$处，电压为0，电流取到最大值$\frac{2V_0^{+}}{Z_0}$
   在终端短路时，传输线上的电压和电流振幅均按正弦变化，根据正弦信号的周期性，在距离负载距离为$\lambda /2$（波长的一半）的整数倍时，电压值为0，而电流值取到最大，这些点被称为电压波节点或电流波腹点。同样，我们根据正弦信号波形的形状也可以知道在$\lambda /4$的奇数倍处电压取到最大值，此时电流为0，这些点被称为电压波腹点或电流波节点。
   进一步，我们根据电流和电压的表达式可以知道短路状态下，传输线上各处的输入阻抗为：
   
   传输线上任意一点均呈电抗特性，在前$1/4$波长内，无耗传输线表现为纯容抗，随后的$1/4$波长内表现为纯感抗，以此为周期循环。
2. 终端开路，$Z_L\to \infty ，{\tau }_L=1$
   同终端短路时的情形类似，此时传输线上的功率为纯虚数，传输线上任意位置的功率为0：
   阻抗与位置坐标$z$的关系为余切(cot=1/tan)，与终端短路的情况类似，传输线上式交替的纯容抗和感抗。

3.6.3 行驻波（混合波）状态

当终端阻抗与传输线特征阻抗不匹配时就一定会出现反射。入射波的能量就无法完全传递到终端负载，反射波与入射波在传输线上叠加，形成行驻波状态。
设负载阻抗为$R_L+j{X}_L$则有：

相位${\varphi }_L$的计算方式为原式整理后虚部和实部的反正切。
传输线沿各点的电流、电压振幅表达式为：

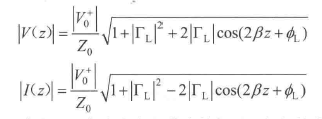
可以看出，驻波的周期为$\frac{\lambda }{2}$（因为$2\beta z$中的2）。同样也存在波节点和波腹点，电压幅度最大时电流幅度取最小，两者恰好相反。

3.6.4 无限长均匀无耗传输线

无限长均匀无耗传输线上电压和电流的表达式为：
考虑一特征阻抗为$Z_0$的传输线连接到特征阻抗为$Z_l$的负载传输线*。若负载传输线与传输线的阻抗匹配或负载传输线无限长则没有来自终端的反射(即不考虑真负载阻抗不匹配所造成的反射，因为反射波在无限长负载传输线上已经衰减殆尽)。那么在连接处的反射系数求解为:
并非所有的入射波都被反射，其中有一些由传输线传递到负载传输线上。

在上图中，左侧是传输线，右侧是负载传输线。在传输线上，电压可以表示为：
在负载传输线上，因为没有来自负载的反射，只有通过连接点继续正向传播的入射波分量，分量占入射波（因为是无耗传输线，连接处信号没有衰减，仍然为入射波）的比重由传输系数$T$给出：
利用边界条件，上面两式在z=0处相等，传输系数和反射系数的关系为：

3.7 广义无耗传输线的求解

3.7.1 两端都出现阻抗失配

通常，我们主要关注负载对传输线上电压和电流的影响，但是位于传输线另一端的波源内阻抗对传输线上波的传播也具有重要作用。事实上最普遍的情况是电路两端都存在阻抗失配的问题。
考虑一段特征阻抗为$Z_0$，长度为$l$的无耗传输线，由$z=0$处内阻为$Z_S$的信号源激励，且在$z=l$处，接阻抗为$Z_L$的负载。
参考上图，根据公式

我们可以知道在输入端和输出端的边界条件有：

1. 输入端($z=0$)
   $$\begin{gathered} V_i=V_0^{+}+V_0^{-}=V_S-I_i{Z}_S \\ {I}_i=\frac{V_0^{+}-V_0^{-}}{Z_0} \end{gathered}$$

2. 输出端($z=l$处)
   $$\begin{gathered} V_L=Z_L{I}_L \\ {I}_L=\frac{V_0^{+}{e}^{-j\beta l}-V_0^{-}{e}^{-j\beta l}}{Z_0} \end{gathered}$$

3. 在传输线的中间位置我们也可以得到
   $$\begin{gathered} 令：V^{+}(z)=V_0^{+}{e}^{-j\beta z};V^{-}(z)=V_0^{-}{e}^{j\beta z} \\ V(z)=V^{+}(z)+V^{-}(z)=V_0^{+}{e}^{-j\beta z}[1+\tau (z)] \\ I(z)=I^{+}(z)-I^{-}(z)=\frac{V_0^{+}}{Z_0}{e}^{-j\beta z}[1-\tau (z)] \end{gathered}$$
   式中，
   
   这里我们类比负载端，利用边界条件也可以得到发送端的反射系数:
   
   忽略中间的纯数学推导过程，直接看结果。
   即，当发送端和接收端都有阻抗失配时，反射波会像在山谷中一样来回反射，每次反射除的衰减由到达两端各自的衰减系数决定，同样也会存在相位变化，为$e^{-j\beta l}$。
   对比再来看电流在输入和接收端阻抗失配时传输线上的反射情况：
   
   
   可以看到电流每次反射除了相位的变化还有反射系数所造成的衰减和电压的反射衰减过程类似。
   
   信号电压和电流在源端和负载端均出现失配的情况下，传输线上信号电压和电流的叠加情况如下图所示：

3.7.2 两端均阻抗匹配

这种情况下，传输线上不存在驻波，因为源端内部阻抗$Z_S$的存在，到达负载端的电压和电流的幅值均减半。

3.7.3 仅源端端匹配

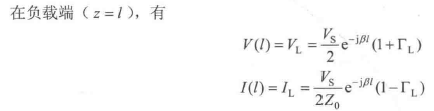
3.7.4 仅负载端匹配

这种情况下，仅表现为源端内阻$Z_S$和传输线特征阻抗之间的分压关系。