【C++二维前缀和】黑格覆盖_在一张由 m * n 个小正方形格子组成的矩形纸张上, 有 k 个格子被涂成了黑色。给-优快云博客

文章讲述了在一个给定的M*N小正方形网格中，有k个黑格子，如何使用一张m*n的矩形卡片找到覆盖最多黑格子的方法。通过计算和比较不同区域的黑格子数量，确定卡片的最大覆盖范围。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

在一张由 M * N 个小正方形格子组成的矩形纸张上，有 k 个格子被涂成了黑色。给你一张由 m * n 个同样小正方形组成的矩形卡片，请问该卡片最多能一次性覆盖多少个黑格子？

输入

输入共 k+1 行：
第 1 行为 5 个整数 M、N、m、n、k，其含义如题目所述。
接下来 k 行，每行 2 个整数，分别表示被涂成黑色的格子的行、列坐标。

输出

输出共 1 行，1 个整数，表示卡片一次性最多能覆盖的黑格子数。

样例输入 Copy

3 5 2 2 3 1 1 2 2 3 5

样例输出 Copy

提示

根据样例数据所得到的涂完黑格的矩形和用于覆盖的矩形如下图所示：

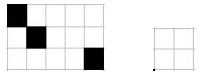
对于 40%的数据：m=n；
对于 100%的数据：M、N、m、n、k 均小于等于 1000，所有黑格不重复出现。

#include <cstdio>
#include <algorithm>
using namespace std;

bool a[1005][1005];
int cnt1[1005][1005], cnt2[1005][1005];

int main()
{
    int M, N, m, n, k, ans = 0;
    scanf("%d%d%d%d%d", &M, &N, &m, &n, &k);
   
    int x, y;
    while (k--)
    {
        scanf("%d%d", &x, &y);
        a[x][y] = 1;
    }
    
    for (int i = 1; i <= M; i++)
        for (int j = 1; j <= N; j++)
            cnt2[i][j] = cnt2[i][j - 1] + a[i][j];
    
    for (int i = 1; i <= M; i++)
        for (int j = 1; j <= N; j++)
            cnt1[i][j] = cnt1[i - 1][j] + cnt2[i][j];
        
    int m1 = min(m,M), n1 = min(n,N);
   
    for (int i = m1; i <= M; i++)
        for (int j = n1; j <= N; j++)
            ans = max(ans, cnt1[i][j] - cnt1[i][j - n1] - cnt1[i - m1][j] + cnt1[i - m1][j - n1]);
    
    for (int i = n1; i <= M; i++)
        for (int j = m1; j <= N; j++)
            ans = max(ans, cnt1[i][j] - cnt1[i][j - m] - cnt1[i - n][j] + cnt1[i - n][j - m]);
    
    printf("%d\n", ans);
    return 0;
}