树状数组入门

1 树状数组

1.1 引例导入

有$n$个数据$a_1,a_2\cdots ,a_n(1\le n\le 10^6)$, 有$m$个操作$(1\le m\le 10^6)$, 每个操作为以下两种之一
1 x 表示查询${\sum }_x^{i=1}a[i]$
2 x y 表示把a[x]修改为y

用普通数组做修改为$O(1)$, 查询为$O(n)$
用前缀和做修改为$O(n)$, 查询为$O(1)$
用暴力或前缀和做都会超时, 我们就要用到树状数组

1.2 简介

树状数组可应用于单点修改, 区间求和
单次修改和查询时间复杂度都为$O(\log n)$, 空间复杂度为$O(n)$

2 使用方法

2.1构建

假如我们把$a$数组看成是完全二叉树的叶子, 构建出树, 在把所有节点向右靠, 就得到以下图形

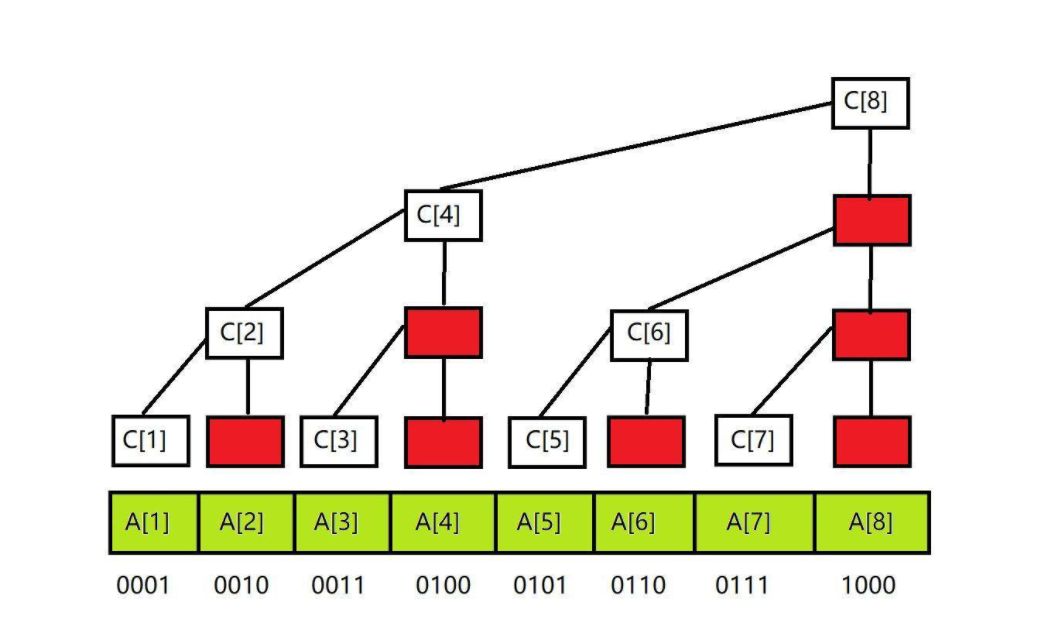
有人可能会奇怪, 为什么这棵树红色的节点不用来存东西
可以通过每一位的二进制看出$c_i$的层数取决于$i$二进制末尾有多少$0$, 而$0$的数量可以用最后的一位$1$算出, 我们就需要找出最后的$1$

int lowbit(int x){
	return x & (-x);
}

正确性证明: 设$x$的末$k-1$位是$0$, 第$k$位是$1$
转成负数的反码后, 第$k$位是$0$, 末$k-1$都是$1$
$+1$变成补码后, 第$k$位是$1$, 其他位正好与$x$取反, 证明完毕
$c_x$要表示的数是${\sum }_{i=x-lowbit(x)+1}^x{a}_i$, 也就是从$c_x$向前数$lowbit(x)$个数

2.2 修改

从图中可以找出以下规律: $i+lowbit(i)$正好是$i$的父节点, 所以我们修改$a_i$, 所有$i$的祖先都要进行修改, 就可以顺着$i$一直往上找到根节点进行修改

void update(int x, int val){  //x是节点编号, val是要修改的值
	for(;x <= n;x += lowbit(x))
		c[x] += val;
}

2.3 查询

我们要进行查询${\sum }_{i=1}^7{a}_i$的值, 发现$su{m}_7=c_7+c_6+c_4$, 而$764$这三个数的二进制为$111110100$, $7-lowbit(7)=6$, $6-lowbit(6)=4$, 所以只需要每次减去$lowbit(i)$求和, 就可以得出结果

int query(int x){  //查询a[1]到a[x]的和
	int res = 0;
	for(;x;x -= lowbit(x))
		res += c[x];
	return res;
}

3 例题

3.1 逆序对

3.1.1 题目思路

求逆序对, 也就是求前面的数比后面的数大, 可以每输入一个数$x$就查询比$x$小的数累加到答案, $1\le a_i\le 10^9$, 要用到离散化

3.1.2 AC代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <map>
using namespace std;

const int N = le6;
long long a[N]，b[N]，c[N]，ans;
int n, x;
map<int, int> mp;

int lowbit(int);
void update(int, int);
long long query(int);

int lowbit(int x){
	return x & (-x);
}
void update(int x){
	//把a[x]增加1
	while(x <=n){
	c[x]++;
	x += 1owbit(x);
}
long long query(int x){
	// 求a[1] + a[2] + ... + a[x]
	long long res = 0;
	while(x >0){
		res += c[x];
		x -= 1owbit(x);
	}
	return res;
}
int main(){
	scanf("%d", &n);
	for(int i = 1;i <= n;i++){
		scanf("%11d", &a[i]);
		b[i] = a[i];
	}
	sort(b+1, b+n+1);
	for(int i = 1;i <= n;i++){
		mp[b[i]] = i;
	}
	for(int i = 1;i <= n;i++){
		x = mp[a[i]];
		update(x);
		ans += i - query(x);
	}
	printf("%11d\n", ans);
	return 0;
}

3.2 BIT-2

3.2.1 题目大意

给定有$n$个元素的数组$a$, 进行$q$次操作, 有两种操作:
1 l r k : 将$a_l$到$a_r$每个数$+k$
2 k : 输出$a_k$

3.2.2 题目思路

用差分思想, $c$表示差分数组, $update$时把$c_l$到$c_r$加$k$, $query$时计算$c_k$的前缀和

3.2.3 AC代码

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;

const int N = 1e6 + 5;
int n, q;
ll c[N];

int lowbit(int x){
	return x & (-x);
}
void update(int l, int r, int k){
	for(;l <= n;l += lowbit(l))
		c[l] += k;
	for(r++;r <= n;r += lowbit(r))
		c[r] -= k;
}
ll query(int k){
	ll res = 0;
	for(;k != 0;k -= lowbit(k))
		res += c[k];
	return res;
}

int main(){
	scanf("%d %d", &n, &q);
	int t;
	for(int i = 1;i <= n;i++){
		scanf("%d", &t);
		update(i, i, t);
	}
	int op, l, r, k;
	while(q--){
		scanf("%d", &op);
		if(op == 1){
			scanf("%d %d %d", &l, &r, &k);
			update(l, r, k);
		}
		else if(op == 2){
			scanf("%d", &k);
			if(k == 0)	printf("0\n");
			else	printf("%lld\n", query(k));
		}
	}
	return 0;
}

3.3 BIT-3

3.3.1 题目大意

给定有$n$个元素的数组$a$, 进行$q$次操作, 有两种操作:
1 l r k : 将$a_l$到$a_r$每个数$+k$
2 l r : 输出$a_l$到$a_r$的和

3.3.2 题目思路

${\sum }_{i=l}^r{a}_i={\sum }_{i=l}^r{\sum }_{j=1}^i{c}_i$
$\because a_1=c_1,$
$a_2=c_1+c_2,$
$a_3=c_1+c_2+c_3,$
$a_4=c_1+c_2+c_3+c_4,$
$\cdots \cdots$
$\therefore {\sum }_{i=l}^r{\sum }_{j=1}^i{c}_i={\sum }_{i=l}^r{c}_i\ast (l-i+1)=(l+1)\ast {\sum }_{i=l}^r{c}_i-{\sum }_{i=l}^r{c}_i\ast i$
所以我们只需要维护两个数组$c_i$和$su{m}_i=c_i\ast i$

3.3.3 AC代码

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;  //等效于 define ll long long

const int N = 1e6 + 5;
int n, q;
ll c[N], sum[N];

int lowbit(int x){
	return x & (-x);
}
void update(int l, int r, int x){
	for(int i = l;i <= n;i += lowbit(i)){
		c[i] += x;
		sum[i] += x * l;
	}
	for(int i = r + 1;i <= n;i += lowbit(i)){
		c[i] -= x;
		sum[i] -= x * (r+1);
	}
}
ll query(int l, int r){
	ll res1 = 0, res2 = 0;
	for(int i = l;i != 0;i -= lowbit(i)){
		res1 += c[i] * l;
		res2 += sum[i];
	}
	for(int i = r + 1;i != 0;i -= lowbit(i)){
	    res1 += c[i] * (r + 1);
		res2 += sum[i];
	}
	return res1 - res2;
}

int main(){
	scanf("%d %d", &n, &q);
	int t;
	for(int i = 1;i <= n;i++){
		scanf("%d", &t);
		update(i, i, t);
	}
	int op, l, r, k;
	while(q--){
		scanf("%d", &op);
		if(op == 1){
			scanf("%d %d %d", &l, &r, &k);
			update(l, r, k);
		}
		else if(op == 2){
			scanf("%d %d", &l, &r);
			printf("%lld\n", query(l, r));
		}
	}
	return 0;
}

3.4 其他例题

火柴排队
和逆序对差别不大

虔诚的墓主人
比较难了

感谢观看
此篇文章为可达鸭Y1第5和第6节课介绍