Codeforces Round 895 (Div. 3) 补题报告

1. 比赛报告

共7题, 第1题AC, 第2题AC, 第3题WA, 第4题CE, 5-7题没做
本篇题解只提供前5道题

2. 比赛过程

第1题 直接AC
第2题 直接AC
第3题 考虑复杂了, 编的代码太乱, 直接跳过
第4题 还是考虑太复杂了, 编译时没注意到错误

3. 题解

3.1 A. Two Vessels

3.1.1 题目大意:

有两个容器里面分别有$a$, $b$克水, 还有个杯子为空, 最多能装$c$克水
可以用杯子从任意一个容器舀出小于等与$c$克水, 倒入另一个容器里
要使两个容器水量相等, 最少需要几次移动

3.1.2 当时思路:

使$x=(\max (a,b)-\min (a,b))/2$
如果$x\%c==0$, $ans=x/c$
否则$ans=x/c+1$

3.1.3 题目解析:

$a$和$b$的差是$abs(a-b)$
输出$ceil(abs(a-b)/2.0-/c)$即可

3.1.4 AC代码:

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int main(){
	int t;
	int a, b, c;
	scanf("%d", &t);
	while(t--){
		cin>>a>>b>>c;
		cout << ceil(abs(a-b)/2.0/c) << '\n';
	}
	return 0;
}

3.2 The Corridor or There and Back Again

3.2.1 题目大意:

一条走廊有无数个房间, 每穿越一个房间需要1秒, 有$n$个陷阱, 第$i$个陷阱在$d_i$房间里, 会在进入房间$s_i$秒后触发, 不可穿过已触发陷阱的房间, 需要从第一个房间到第$k$个房间再返回, 问最大的$k$是多少

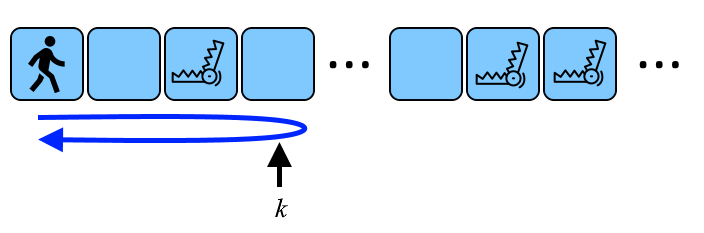
例: 当$n=1,d_1=2,s_i=2$时, 当到达第$3$个房间又返回第$2$个房间时陷阱触发, 无法到达第$1$个房间, 所以$k=2$

3.2.2 当时思路:

从$1$到$n$, 判断最远能走到哪一个房间, 取最小值即可, 因为到达陷阱正好触发时也不能穿过, 所以$s_i$要$-1$, $ans=\max (ans,d_i+(s_i-1)/2)$

Q: 要求最远到达距离, 为什么要取$\min$呢?
A: 前面的$d_i+(s_i-1)/2$求的就是在第$i$个陷阱的限制下, 最远能走到的地方, 已经是最大值了, 求$\min$是为了满足所有陷阱的要求

3.2.3 题目解析:

同 3.2.2当时思路

3.2.4 AC代码:

#include <iostream>
#include <cstdio>
using namespace std;
const int  N = 105;
int t, n, d, s, k;
int main(){
	scanf("%d", &t);
	while(t--){
		k = 1000;
		scanf("%d", &n);
		for(int i = 1;i <= n;i++){
			scanf("%d %d", &d, &s);
			k = min(k, d + (s - 1) / 2);
		}
		printf("%d\n", k);
	}
	return 0;
}

3.3 Non-coprime Split

3.3.1 题目大意:

有2个整数$l\le r$, 需要找到两个整数$a$, $b$, 满足

• $l\le a+b\le r$
• $\gcd (a,b)\ne 1$

3.3.2 当时思路:

用欧拉筛出$n$以内的素数$p_i$, 便利$x:i\sim n/2$, $y=n-x$
遍历$p$数组, 如果$x\%p_i==0\&\&y\%p_i==0$, 输出$x$和$y$, 结果TLE

3.3.3 题目解析:

定义函数$prime(x)$返回$x$的最小质因子, 素数返回$0$
遍历$i:l\sim r$, 定义$x=prime(i)$, 如果$x\ne 0$, 输出$x$和$i-x$
如果$i$遍历完还没有输出, 那么输出$-1$

3.3.4 AC代码:

#include <iostream>
#include <cstdio>
using namespace std;
int t, l, r;
int prime(int x){
	for(int i = 2;i*i <= x;i++)
		if(x % i == 0)	return i;
	return 0;
}
int main(){
	scanf("%d", &t);
	while(t--){
		bool f = 0;
		scanf("%d %d", &l, &r);
		for(int i = l;i <= r;i++){
			int x = prime(i);
			if(x != 0){
				printf("%d %d\n", x, i - x);
				f = 1;
				break;
			}
		}
		if(!f)	printf("-1\n");
	}
	return 0;
}

3.4 Plus Minus Permutation

3.4.1 题目大意:

输入三个整数$n$, $x$, $y$, 对于排列$p$, 求${\sum }_{i=1}^{\lfloor \frac{n}{x}\rfloor }\max (p[i\cdot x])-{\sum }_{i=1}^{\lfloor \frac{n}{y}\rfloor }\max (p[i\cdot y])$, 也就是所有$i$能被$x$整除的$p_i$之和减去所有$i$能被$y$整除的$p_i$之和的最大值

3.4.2 当时思路:

用欧拉筛出素数, 求出$x$和$y$共有的素数积为$z$, 求$n$往前数$x-z$个数的和 $-$ $1$向后数$y-z$个数的和

3.4.3 题目解析:

让答案尽可能大, 就是让前一项尽可能大, 后一项尽可能小, 也就是$x$倍数位置的数尽可能大, $y$背书位置上的数尽可能小, $lcm(x,y)$位置上的数又被加又被减, 就不用管
设$z=lcm(x,y)$, 求$n$往前数$x-z$个数的和 $-$ $1$向后数$y-z$个数的和

3.4.4 AC代码:

#include <iostream>
#include <cstdio>
typedef long long ll;
using namespace std;
ll t, n, x, y, z, sumx, sumy;

ll lcm(ll, ll);
ll gcd(ll, ll);
ll lcm(ll a, ll b){
	return a / gcd(a, b) * b;
}
ll gcd(ll a, ll b){
	if(a % b == 0)	return b;
	return gcd(b, a % b);
}

int main(){
	scanf("%lld", &t);
	while(t--){
		scanf("%lld %lld %lld", &n, &x, &y);
		z = n / lcm(x, y);
		x = n / x - z;
		y = n / y - z;
		sumx = (n-x+1 + n) * x / 2;
		sumy = (1 + y) * y / 2;
		printf("%lld\n", sumx - sumy);
	}
	return 0;
}

3.5 Data Structures Fan

3.5.1 题目大意:

有$n$个整数$a_1$, $a_2\cdots a_n$, 和一个长度为$n$的二进制字符串(只包含$0$和$1$的字符串)
有$q$次查询, 有两种类型:

• 1 l r 把$s_l$到$s_r$取反
• 2 g 计算所有$s_i=g$下标$i$的数字$a_i$的异或和

3.5.2 当时思路:

暴力

3.5.3 题目解析:

要知道$0\oplus n=n$, $n\oplus n=0$
设$x_0$等于所有$s_i=0$的$a_i$异或和, 设$x_1$等于所有$s_i=1$的$a_i$异或和
对于操作1, 设$x_0=a_1\oplus a_2\oplus a_3\oplus a_4$, 现在$s_1$到$s_3$被取反, 这时我们需要$x_0=x_0\oplus a_1\oplus a_2\oplus a_3$, 把原来的$a_1$到$a_3$抵消掉, 这样$x_0=a_4$, 需要用前缀和优化
对于操作2, 直接输出$x_0$或$x_1$

3.5.4 代码:

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 1e5 + 5;
int n, q, t, c, a[N], tp, l, r, g;
int main(){
	scanf("%d", &t);
	while(t--){
		int sum[N] = {0}, x0 = 0, x1 = 0, x;
		scanf("%d", &n);
		for(int i = 1;i <= n;i++){
			scanf("%d", &a[i]);
			sum[i] = sum[i-1] ^ a[i];
		}
		for(int i = 1;i <= n;i++){
			scanf("%c", &c);
			if(c == '0')	x0 ^= a[i];
			else	x1 ^= a[i];
		}
		scanf("%d", &q);
		while(q--){
			scanf("%d", &tp);
			if(tp == 1){
				scanf("%d %d", &l, &r);
				x = sum[l-1] ^ sum[r];
				x0 ^= x;
				x1 ^= x;
			}
			else{
				scanf("%d", &g);
				if(g == 0)	printf("%d ", x0);
				else	printf("%d ", x1);
			}
		}
		printf("\n");
	}
	return 0;
}

4. 反思

4.1 回顾问题

思路不够好, 基础知识不太巩固。不到最后一刻就不能放弃

4.2 如何改进

多刷题

本文为可达鸭Y1第4课补题报告
感谢观看
2023.10.14 Sat.