机器学习 第六章 支持向量机

6.1 间隔与支持向量

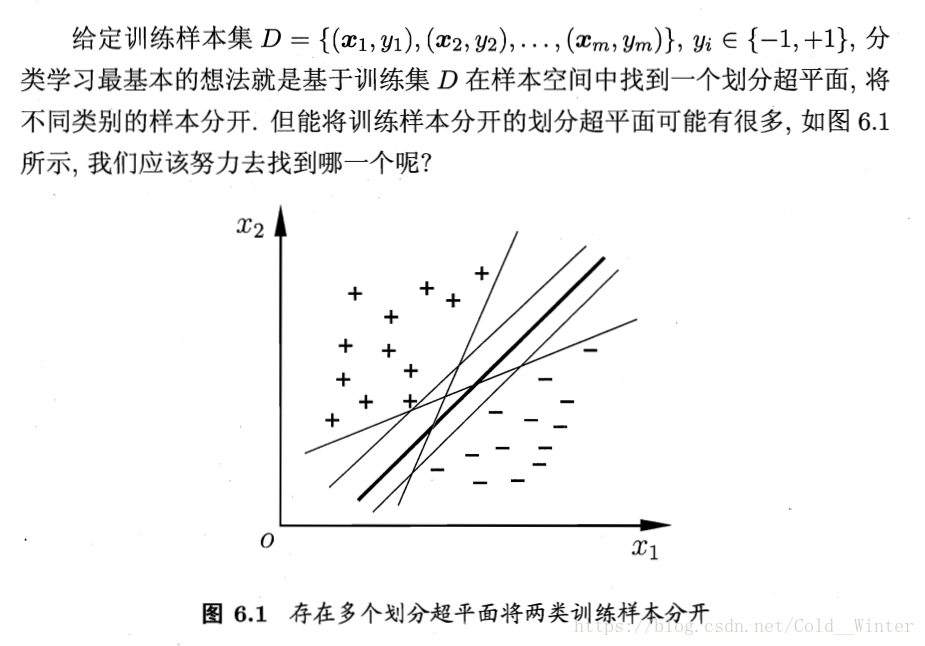
在样本空间中，划分超平面可通过如下线性方程来描述：

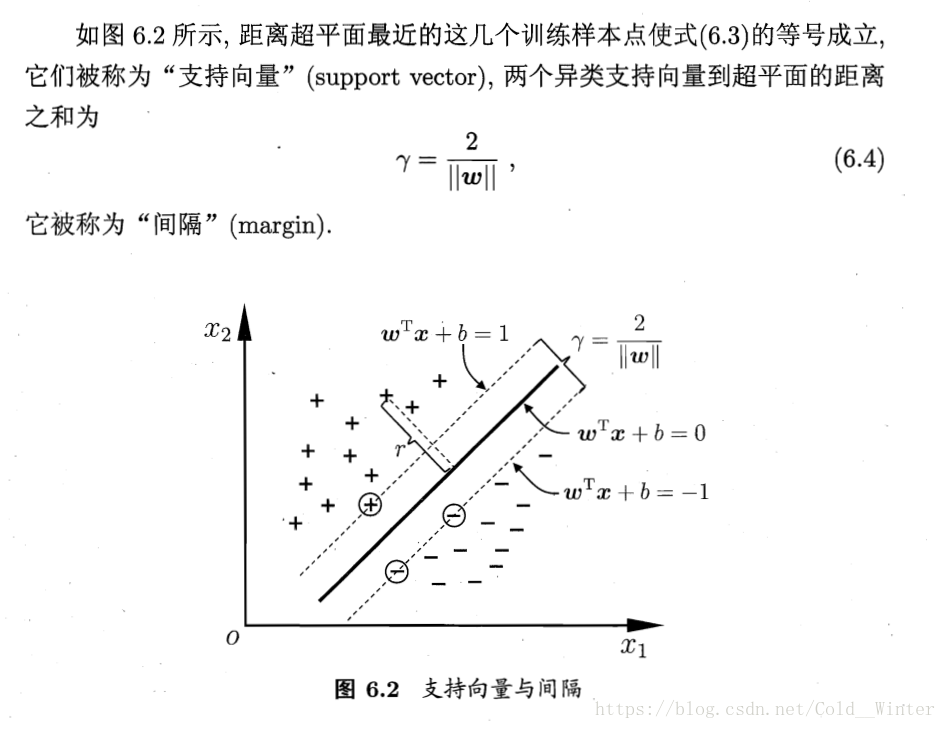
6.2 对偶问题

我们希望求解式（6.6）来得到大间隔划分超平面所对应的模型：

对式（6.6）使用拉格朗日乘子法可得到其“对偶问题”：



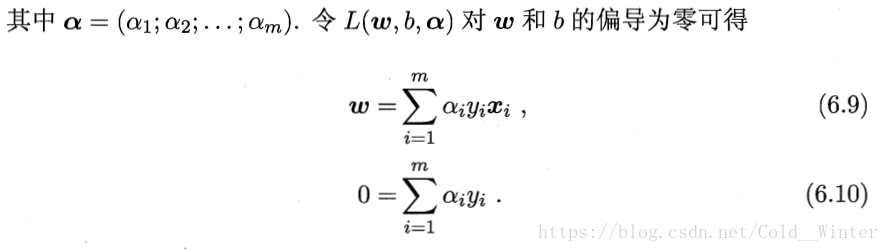
最终解出α，求出w和b可得模型：

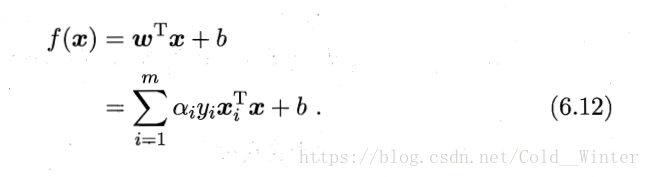
对于求解式(6.6)，有一个著名的高效算法：SMO

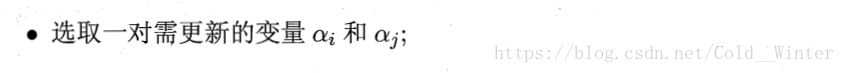
SMO算法之所以高效，恰由于在固定其他参数后，仅优化两个参数的过程能做到非常高效。

6.3 核函数

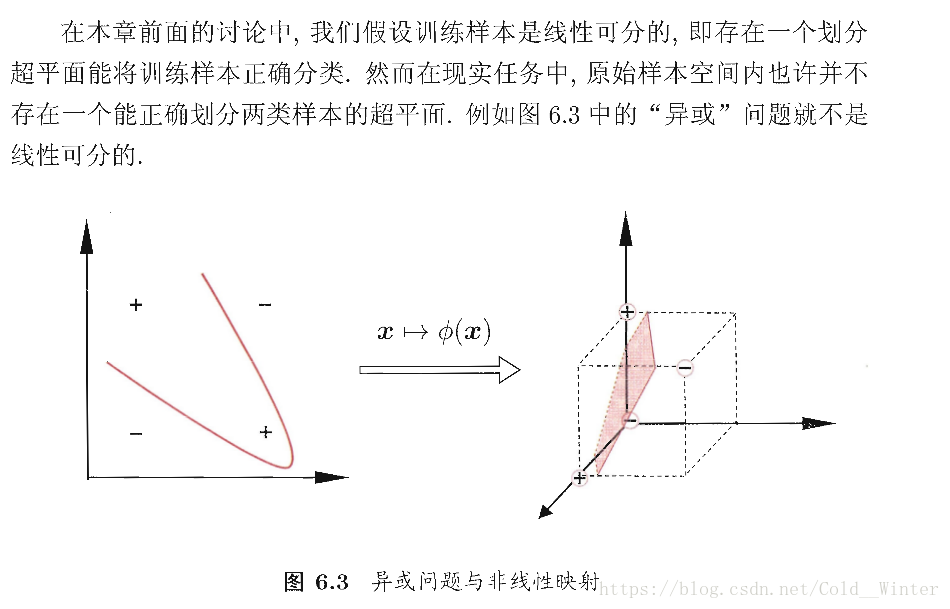
对于这样的问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。图6.3中，若将原始的二维空间映射到一个合适的三位空间，就能找到一个合适的划分超平面。

求其对偶问题，最终求解，即可得到:

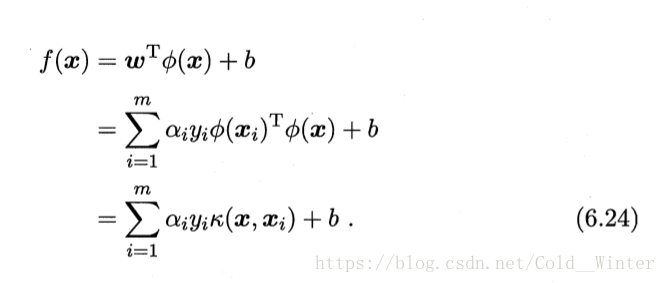
此式显示出模型最优解可通过训练样本的核函数展开，这一展式亦称：支持向量展式

以下列出几种常用核函数

6.4 软间隔与正则化

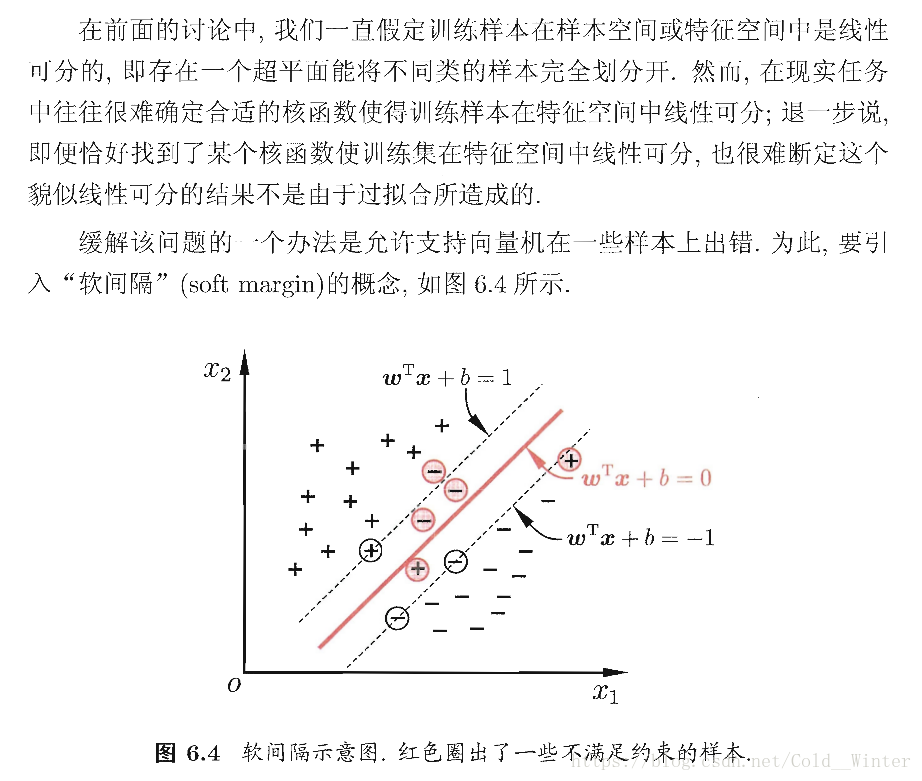
具体来说，前面介绍的支持向量机形式是要求所有样本均满足约束（6.3） 即所有样本必须划分正确，这称为“硬间隔”，而软间隔则是允许某些样本不满足约束


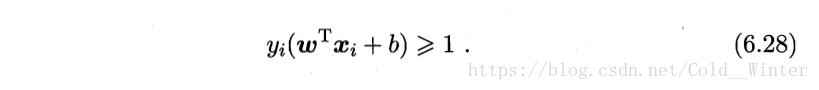
人们一般用其他函数来替代 0/1 损失函数 称为”替代损失”
三种常用的替代损失函数以及图片：


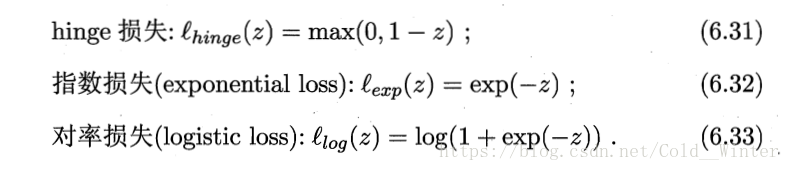
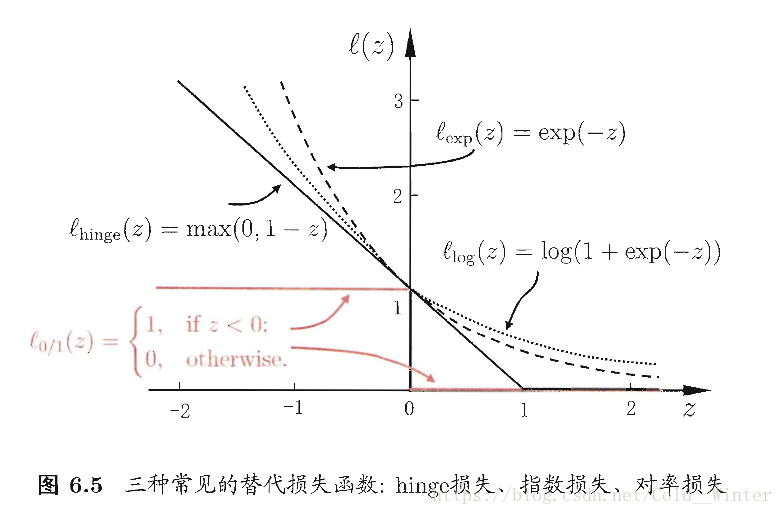
把 式6.29中的0/1损失函数换成别的替代损失函数可以得到其他学习模型，性质与所用函数相关，但都有共性，可以写为更一般的形式：

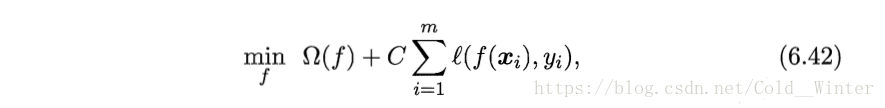
第一项被称为结构风险，用于描述模型f的某些性质，第二项称为经验风险用于描述模型和训练的契合程度；C用于对二者折中。它能表述我们希望获得何种性质的模型，也有助于削减假设空间，降低了最小化训练误差的过拟合风险。从这个角度讲，式6.42称为“正则化”问题，可以使得优化过程趋向与希望目标。

6.5 支持向量回归

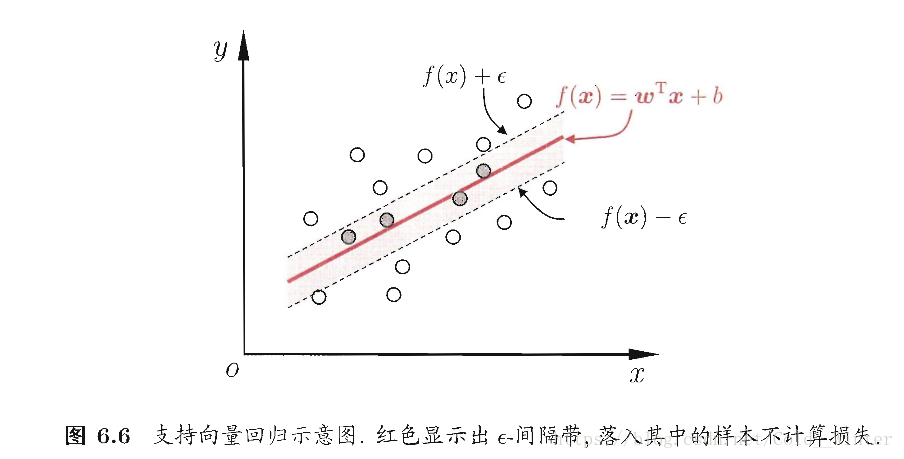
SVR问题可形式化为：


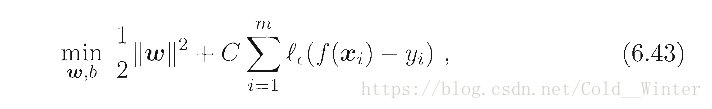
引入拉格朗日子，由拉格朗日子乘法得到拉格朗日函数



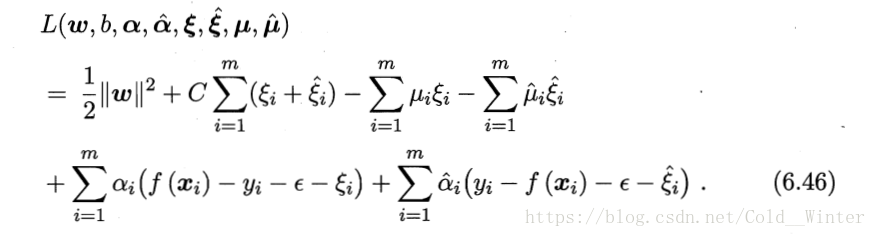
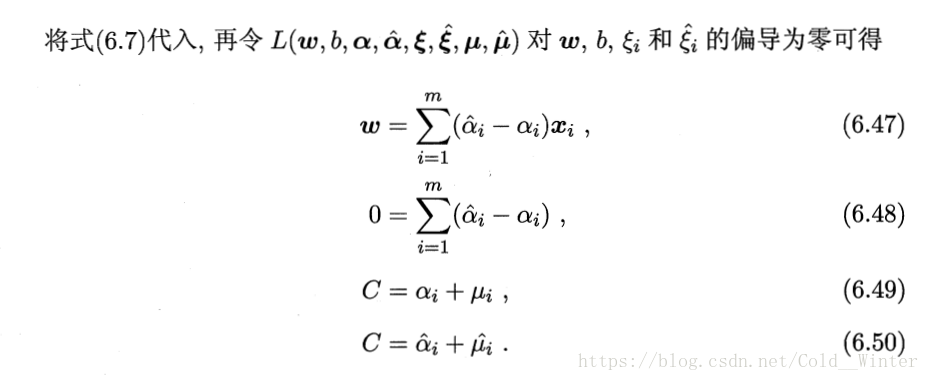
将式6.55带入6.19 则SVR可表示为

6.6 核方法

回顾可发现，给定训练样本，无论是SVM还是SVR学得的模型总能表示成核函数的线性组合。
表示定理表现了更一般的结论：

人们发展出一系列基于核函数的学习方法，统称为“核方法”。最常见的是通过“核化”(即引入核函数)来将线性学习器拓展为非线性学习器。