Coding Practice，48天强训（15）

Topic 1：完全平方数（数学）

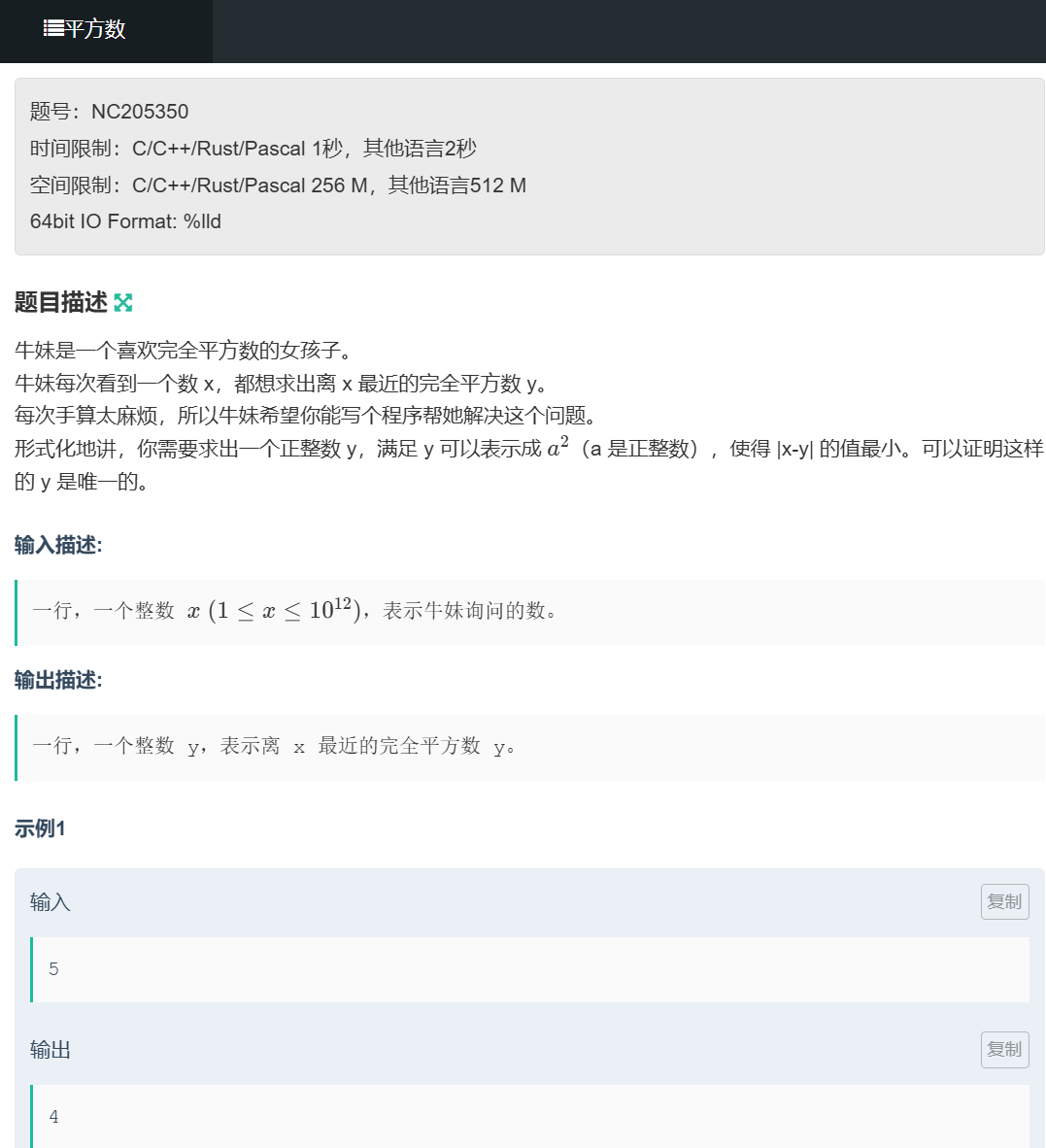
简单题简单做

#include <bits/stdc++.h>
using namespace std;

int main()
{
    long long x;
    cin >> x;
    long long y = sqrt(x);// sqrt开根之后取整
    
    // 4 5 9  1 < 4 所以4离5更近
    cout << (x - y * y < (y + 1) * (y + 1) - x ?
        y * y : (y + 1) * (y + 1)) << endl;
    
    return 0;
}

---

Topic 2：分组（哈希，二分查找）

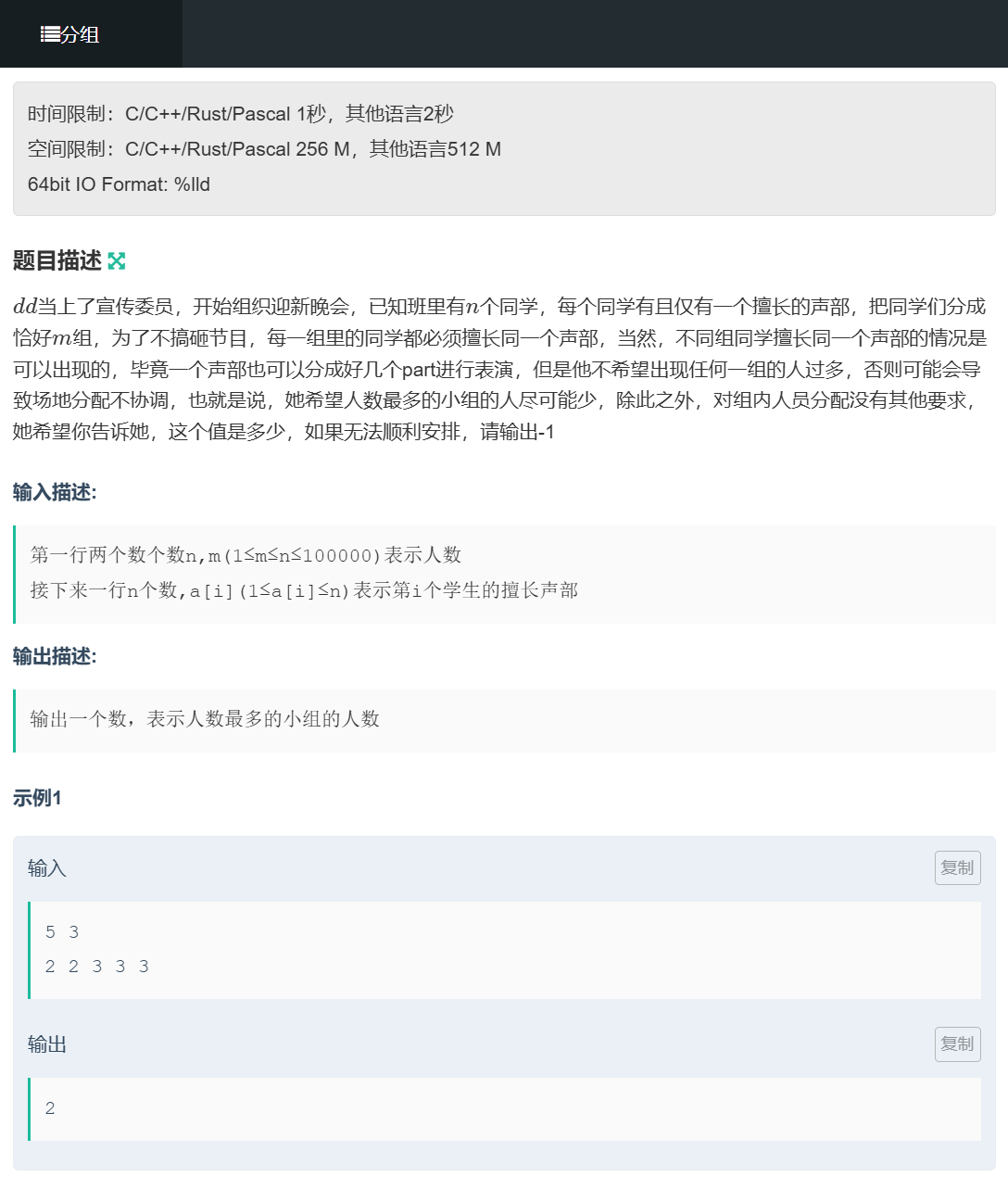
#include <bits/stdc++.h> 
using namespace std;

int main() 
{
    int n, m;
    cin >> n >> m; // 读取同学数量n和分组数量m

    vector<int> v(n); // 存储每位同学擅长的声部
    for(int i = 0; i < n; ++i) cin >> v[i]; // 读取每个同学的擅长声部

    unordered_map<int, int> sta; // 用哈希表统计每个声部的人数（声部 -> 人数）
    for (const auto e : v) sta[e]++; // 遍历同学列表，统计每个声部出现的次数

    int res = -1; // 如果不能合理分组，输出-1
    if (sta.size() > m) // 如果不同声部的数量超过m，无法分成m组
    { 
        cout << res << endl;
        return 0;
    }

    // 尝试找到每组最大人数x，使得可以在m组内合理分配
    for (int x = 1; x <= n; ++x) // 每组人数x从1尝试枚举到n
    {
        int sum = 0; // 记录按照当前x值需要的最少组数
        for (auto &[s, c] : sta) // 对每个声部统计其所需的组数
        {
            // 对于每种声部，将其人数c分成每组x人的小组，需要 (c + x - 1) / x 组
            sum += (c + x - 1) / x;// c/x向上取整公式
        }
        if (sum <= m) // 随着每组人数x不断增大，总组数sum会逐渐减小
                      // 当总组数sum不超过m，说明这个x是可行的
        {
            res = x; // 更新结果为当前x
            break; // 找到最小可行x后即可结束
        }
    }
    cout << res << endl; // 输出答案
}

auto &[s, c] : sta 中的 [s, c] 是 结构化绑定声明（Structured Binding Declaration），是 C++17 引入的一种新语法，用于将结构或 pair/unordered_map 等容器的元素“拆包”成多个变量。

以上是暴力枚举的方法，我们还能采用二分法来优化效率

#include <bits/stdc++.h>
using namespace std;

// 判定函数：当每组最多x人时，是否能在m组内完成所有分组
bool check(int x, unordered_map<int, int> &sta, int m) 
{
    int sum = 0;
    for (auto &[s, c] : sta) sum += (c + x - 1) / x;// 向上取整
    return sum <= m;
}

int main() 
{
    int n, m;
    cin >> n >> m; // 读取同学数量n和最大分组数量m

    vector<int> v(n); // 存储每个同学的声部编号
    unordered_map<int, int> sta; // 统计每个声部的人数（哈希表）

    for (int i = 0; i < n; ++i) 
    {
        cin >> v[i];     // 读取每个同学的声部
        sta[v[i]]++;     // 对应声部人数+1
    }
    if (sta.size() > m) // 声部种类超过组数，无法满足“每组只能有一种声部”的要求
        return cout << -1, 0;// 逗号表达式返回值只会返回后面的0，但前面的cout也会被打印
    
    int l = 1, r = n, res = -1; // 初始化二分左右边界，res记录最小可行值

    while (l <= r) 
    {
        int mid = (l + r) / 2; // 尝试每组人数为mid
        if (check(mid, sta, m)) 
        {
            res = mid;         // mid可行，尝试更小的x
            r = mid - 1;
        } 
        else 
        {
            l = mid + 1;       // mid不可行，需要更多人进一组
        }
    }

    cout << res << endl; // 输出最小可行的每组人数上限
}

Topic 3：拓扑排序

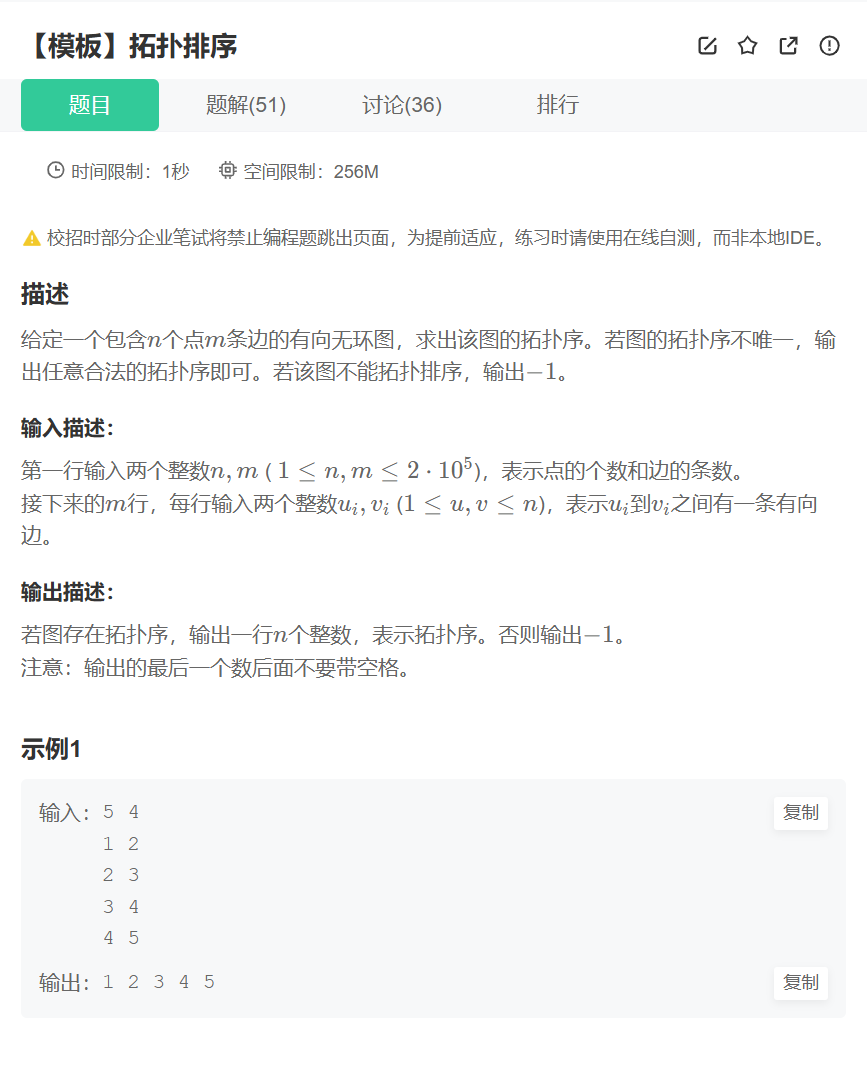
纯考察拓扑排序的一个题目，用BFS解决

#include <bits/stdc++.h>
using namespace std;

int main() 
{
    ios::sync_with_stdio(false); // 关闭 C/C++ 同步，加快 cin cout 速度
    cin.tie(0);                  // 解绑定 cin 和 cout，提高效率

    int n, m;
    cin >> n >> m;              // 读取点数 n 和边数 m

    vector<vector<int>> graph(n + 1); // 邻接表，graph[i] 存所有从 i 出度所指向的点
    vector<int> in_degree(n + 1, 0);  // in_degree[i] 是点 i 的入度，既指向i的边数，初始为 0

    // 读取 m 条边
    for (int i = 0; i < m; ++i) 
    {
        int u, v;
        cin >> u >> v;          // 边 u → v，表示 u 指向 v
        graph[u].push_back(v);  // 将 v 放入 u 的邻接表中（u出度边v）
        in_degree[v]++;         // v 的入度 +1
    }

    queue<int> q;               // 创建一个队列，用于存放所有入度为 0 的点
    vector<int> topo;           // 存放最终的拓扑排序结果

    // 把所有入度为 0 的点先放进队列（它们可以最先被处理）
    for (int i = 1; i <= n; ++i) // 从1开始，对应下标
    {
        if (in_degree[i] == 0) 
        {
            q.push(i);
        }
    }

    // 开始广度优先BFS遍历（拓扑排序核心过程）
    while (!q.empty()) 
    {
        int u = q.front();      // 记录队头元素（当前可以处理的点）
        q.pop();                // 出队头

        topo.push_back(u);      // 加入对头到拓扑排序结果中

        // 遍历 u 出度指向的所有点 v
        for (int v : graph[u]) 
        {
            in_degree[v]--;     // 因为 u 被处理了，所以指向v的边要断开一根
            if (in_degree[v] == 0) 
            {
                q.push(v);      // 如果 v 入度变成 0，说明可以被处理了，加入队列
            }
        }
    }

    // 如果结果中有 n 个点，说明拓扑排序成功
    if ((int)topo.size() == n) 
    {
        for (int i = 0; i < n; ++i) 
        {
            cout << topo[i];       // 输出每一个点
            if (i != n - 1) cout << " "; // 每个点后加空格（最后一个除外）
        }
        cout << "\n";
    } 
    else 
    {
        // 如果没处理完所有点，说明图中有环，不能拓扑排序
        cout << -1 << "\n";
    }

    return 0;
}

拓扑排序比较简单，但是确实很实用，特别是能判断图是否带环。