多源最短路径问题(Floyd-Warshall)

为了求任意两个点之间的最短路径

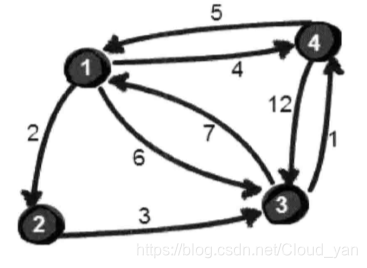
照旧，利用矩阵来存储图的信息
自身到自身，设置为0
无法到达设置为无穷
可以到达的 i 到 j ，就记为a[i][j]=路径长度

思路一：
对所有的两个点动用一次dfs或bfs，也就是n²次DFS或BFS
上述是个啥子方法，只是看看
思路二：
如果，要使得从 i 到 j，就必须经过中转点，i→k→j，那么我们从所有的点中，找到这个k，使得i→j的路径变短
或许，经过更多点，会使得i→j的路径变短，i→k1→k2→···→j，那么我们就需要找到这些k1，k2等等点

首先，我们先求出，经过点1，求任意两点之间的路径，看是否比原本的路径少了

for (i = 1; i <= n; i++)
{
   
   
	for (j = 1; j <= n; j++)
	{
   
   
		if (e[i][j] > e[i][1] + e[1][j])
			e[i]</