数字电路 第六章 时序逻辑电路

时序逻辑电路

特点：
任意时刻的输出不仅与该时刻输入变量的取值有关，而且与电路的原状态，即过去的状态有关。

时序逻辑电路：
包含组合电路和存储电路，存储电路具有记忆功能，通常由触发器构成
存储电路的输出状态Q反馈到组合电路的输入端，与外部输入信号X共同决定组合电路的输出Z。组合电路的输出除了包含外部输出Z，还包含连接到存储电路激励端的内部输出Y，它将控制存储电路的状态变化。

时序逻辑电路结构框图：

X：外部输入信号
Q：存储电路的状态输出，也是组合电路的内部输入
Z：外部输出信号
Y：存储电路的激励信号，也是组合电路的内部输出

在存储电路中，触发器的每一位输出q称为一个状态变量，j个状态变量可以组成2^j个不同的内部状态。

4组信号的逻辑关系表示：
输出方程：Zⁿ = F(Xⁿ,Qⁿ)
激励方程：Yⁿ = G(Xⁿ,Qⁿ) ---------(驱动方程)
状态方程：Qⁿ⁺¹ = H(Yⁿ,Qⁿ)

表明：
时序电路的某一时刻Zⁿ和存储电路的激励Yⁿ仅仅与当前时刻的外部输入和内部状态有关。均为组合电路的输出
存储电路的次态由激励Y和存储电路原状态决定

时序电路的工作过程实质上就是在不同的输入条件下，内部状态不断更新的过程

时序电路的分类

按状态变化分：
同步时序电路：电路状态的变化在同一时钟脉冲作用下发生，即各触发器状态的转换同步完成
异步时序电路：不使用同一个时序脉冲信号源，即各触发器状态的转换是异步完成的。

按输出信号特点分：
米里型时序电路(Mealy)：某时刻的输出取决于该时刻的外部输入和内部状态
摩尔型时序电路(Moore)：某时刻的输出只取决于该时刻的内部状态，不受当时输入的影响或没有输入变量。但当输入变化后，必须等待时钟的到来状态变化时才能导致输出变化。
因此Moore比Mealy的输出要晚一个时钟周期

时序逻辑电路的功能描述

1. 逻辑方程式
2. 状态转移表：
   Mealy型：
   
   Moore型：
   
   特殊Moore型：
   
3. 状态图
   Mealy型：外部输出在转移条件中给出
   
   Moore型：外部输出在圆圈内指明
   
4. 时序图

---

同步时序电路分析

分析方法：

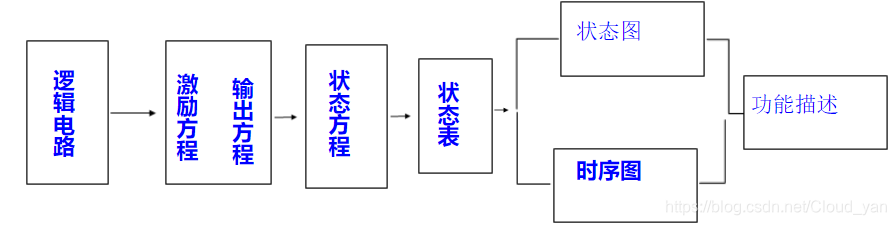
先写出各个的逻辑方程式
Q₁ | Q₂ | Q₃
Q₁ⁿ⁺¹ | Q₂ⁿ⁺¹ | Q₃ⁿ⁺¹ | Z

逻辑方程表达式：
右边一定是现态，不可能出现次态
次态是输入激励信号的作用下，将要到达的状态，也就是说，不存在，将要存在。

有效状态：一个闭合回路。在电路正常工作时，状态总是按照这个闭合里的序列循环变化。通常称处于这个序列循环的状态为有效状态。该循环为有效循环或主循环
无效状态：不处于主循环的其他状态，即使也是一个循环，也不是有效状态

如果一个时序电路中所有的无效状态都能通向有效序列，则成该电路有自启动能力

计数器

定义：有状态闭合环的时序电路
例如：该时序电路状态转移按00→01→10→11→00→···循环变化，实现了模4加法计数器功能

序列信号发生器

定义：能输出一个周期序列的电路
电路特点：一般无输入X，有输出Z，属于特殊Moore型电路
结构：实质上是一个模为N的计数器加上一个组合电路构成，设周期序列01的个数是N

序列线号检测器

当X连续输入三个1之后，Z输出一个1。这是代表了连续输入了三个1

脉冲分配器

在CP脉冲作用下，把宽度为T的脉冲依次分配给Q0，Q1和Q2各端

---

同步时序电路设计

根据设计要求
写出状态表
用卡诺图化简状态，得到状态方程
根据状态方程，选择触发器
画出电路图

---

计数器的设计

计数器是一个周期性的时序电路，其状态图有一个闭合环，闭合环循环一次需要的时钟脉冲个数称为计数器的模值M。由n个触发器构成的计数器，其模值M一般应满足2^n-1<M≤2ⁿ
例如：
设计一个模5计数器
状态变化为000→001→011→101→110→000循环往复
分析：有至少5个状态，因此需要三个触发器
依据上述状态，构建状态图(不在上述存在的状态，标记为X)
凭借卡诺图化简，得到状态方程。
自启动检查
依据状态方程选择触发器
构建电路

特别提醒：
如果题目要去用JK触发器的话，那么在化简卡诺图的时候，要对状态图进行划分。便于获得J、K的状态方程

---

序列信号发生器的设计

序列信号发生器是一个能输出周期序列的电路
设计思路：
根据要设计的序列中的01个数N，先设计一个模值为N的计数器
计数器中每个状态对应一个输出的序列值

例如：
设计能产生01011的序列发生器
分析：
设计数器的状态变化为：
000→001→011→101→110→000循环往复
要发生一个周期序列包含5个不同的状态；
先设计一个模5的计数器，让每个有效状态对应一个序列中的状态数。因此所需触发器有3个
根据序列，把Z对应与有效状态的表现，规划好(即Z就是每个状态下对应的输出的序列中的每个0或1值)
根据上述，列出状态表
利用卡诺图进行化简
得到状态方程，并选择触发器
得到电路图

例如：
建立"111"序列检测器的电路
分析：111表明至少有3个状态，所以需要两个触发器。
选择其中的3个状态，分别对应一个1，多余的状态对应0

非给定状态时序电路设计步骤

1. 根据设计要求，设计状态和状态转换
2. 精简状态表，状态分配
3. 得到状态方程
4. 画出电路图

详细理论：

步骤1

分析题意，确定输入输出变量
设置状态，首先确定有多少种信息需要记忆，然后对每种需要记忆的信息设置一个状态并用字母表示
确定状态之间的转换关系，画出原始状态图，列出原始状态表

原始状态图可能包含多余的状态

步骤2

化简的核心是找等价状态
等价状态的定义：
对两个状态S_i和S_j，如分别以之为初始状态，加入任意的输入，电路均产生相同的输出，称S_i和S_j等价

等价状态可以合并

判断等价状态的条件

1. 相同的输入有相同的输出
2. 相同的输入时，次态等价，次态等价指：
   1. 次态相同
   2. 次态交错
   3. 次态互为隐含条件

一个栗子：

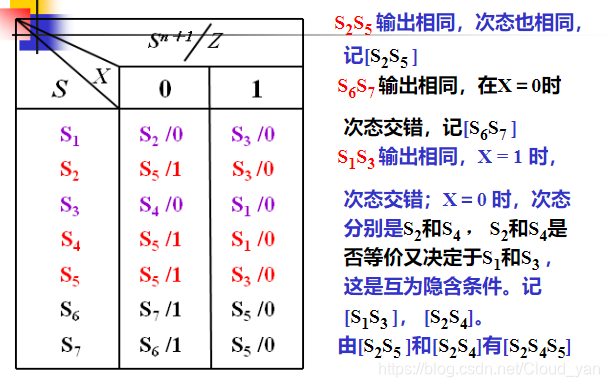
会了这个，其他的也就会了。一般推广特殊

我们知道：
等价状态具有传递性
若S_i和S_j等价，S_i和S_k等价，则S_j和S_k等价

相互等价的状态的集合称为等价类
凡是不被其他等价类所包的等价类称为最大等价类
如果某一状态和其他状态都不等价，则其本身就是一个最大等价类

状态表的化简，就是寻找所有最大等价类，并将最大等价类合并，最后得到最简状态表

如果我们就是只靠眼去找最大等价类，那么是很容易出现错误的，那么我们有以下方法
隐含表化简
一般看两遍：顺序比较，关联比较

顺序比较，也就是A和B比较，A和C比较，A和D比较·····
对原始状态表的每一对状态逐一比较：

1. 状态对肯定不等价，标记X
2. 状态对肯定等价，标记√
3. 状态对是否等价取决于隐含条件，把隐含条件填入，需之后进一步比较

关联比较：对顺序比较中需要进一步比较的状态进行比较
也就是看那些需要看隐含条件的
如果隐含条件等价，那么这两也等价

之后，就是找最大等价类
然后列出最简状态表

状态分配，随便分，想怎么分怎么分

状态分配只需要注意有几个状态，根据此选择二进制位数罢了

状态都有了，之后就是确定状态方程

自启动检查

例题：
用JK触发器设计111序列检测器
分析：

根据设计要求，设计状态

得到原始状态表

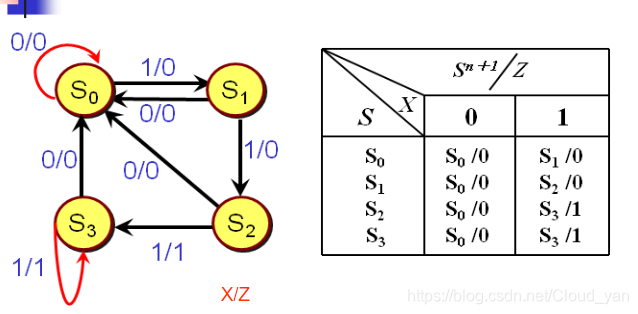
精简状态表

状态分配

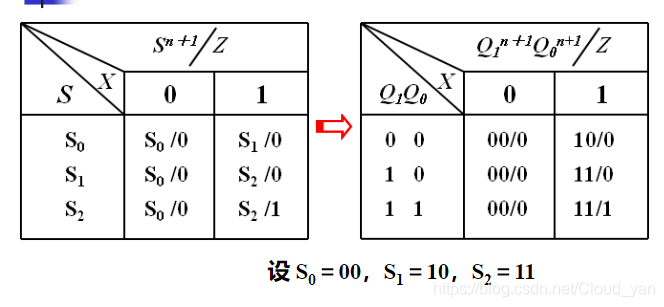
得到激励方程


自启动检查

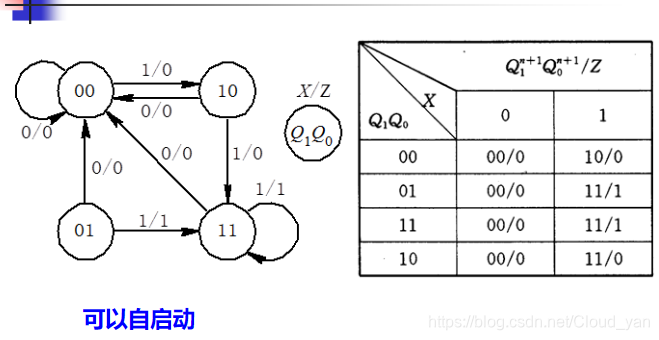
如果无法自启动，则需要进行重新圈卡诺图
新圈法将克服死循环，也不增加激励函数的复杂程度

画出电路图

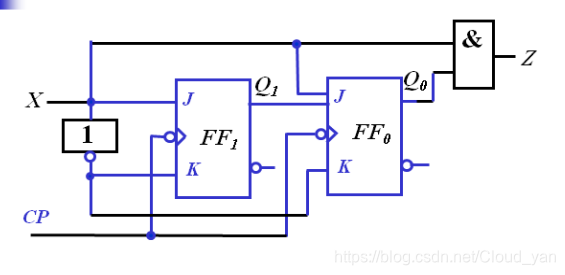
计数器

计数器的应用：
对输入脉冲进行计数、分频，定时，顺序控制及产生其他时序信号。

计数器是一个周期性的时序电路，在时钟信号的不断作用下，电路的状态按一定的顺序循环变化。循环一次所需要的时钟脉冲的个数称为计数器的模值M。计数器在计数值达到其最大容量(模M)时会产生一个进位信号，因此有时把模M计数器称为M进制计数器。

计数器的划分：
按时钟控制：异步、同步
按计数过程中数值的增减：加法计数器、减法计数器和可逆计数器
按计数器状态的数制和编码方式：二进制计数器、非二进制计数器、移位型计数器

同步二进制计数器和同步十进制计数器

同步二进制计数器

同步二进制计数器通常用n位T触发器构成，模值M=2ⁿ

同步十进制计数器

十进制计数器由4位触发器构成，用10个状态组成计数循环。
BCD计数器

集成计数器

集成计数器具有功能较完善，通用性强，功耗低，工作速率高而且可以方便进行扩展的优点。

集成计数器的功能描述

输入端：
计数脉冲输入：CP
控制输入：
同步或异步清0：Cr
同步或异步预置：LD(LOAD)和并行预置数输入D/C/B/A
计数使能：P、T
加减控制端：U/D

输出端：
状态输出：Q_DQ_CQ_BQ_A
进位输出，借位输出：O_c，O_B

4位二进制计数器74LS161、74LS163

74LS161：
模2⁴同步集成计数器，具有计数、保持、预置和清零的功能
逻辑符号：

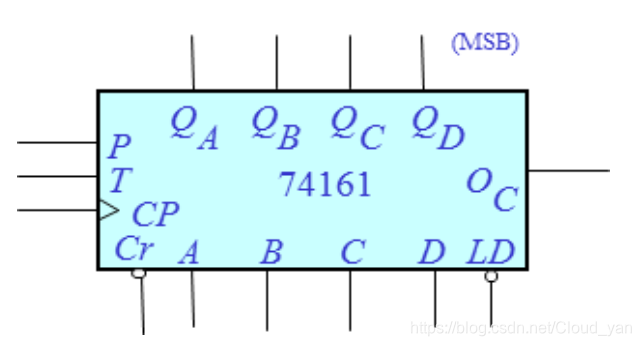
异步清0端 Cr：低电平有效且与CP无关
同步预置端 LD：低电平有效
计数允许控制端P、T：高电平有效。P/T有一个为低时，各触发器的J、K端均为0，从而使计数器处于保持状态。P和T的区别是：T影响O_c，P不影响。
置数输入端：A、B、C、D:CP上升沿置数有效
计数脉冲输入端：CP上升沿有效
进位输出端：O_c=Q_DQ_CQ_BQ_AT，仅当T=1且计数状态为1111时，O_c才为高，并产生进位信号

74LS163与74LS161的区别是74LS163为同步清0，即C_r=0，当CP上升沿到来时，才能清0。

同步集成十进制计数器

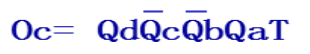
74LS160：异步清0
74LS162：同步清0

4位二进制同步加/减计数器74LS169

加/减计数器称为可逆计数器
计数器的加、减由控制端的输入电平决定，则这种电路称为单时钟结构
若计数器的加、减分别由两个时钟信号源控制，则这种电路称为双时钟结构

74LS169：
U/D为加减控制端，当U/D=1时进行加法计数，当U/D=0时，进行减法计数
在加法计数进入1111状态后，O_c端有负脉冲输出；
在减法计数进入0000状态后，O_c端有负脉冲输出

十进制同步加/减计数器

74LS168单时钟结构
在加法计数进入1001状态后，进位输出O_c有负脉冲输出，宽度为一个时钟周期

---

集成计数器的级联

将多片(或称多级)集成计数器进行级联可以扩大计数范围

级联方式：异步级联，同步级联

异步级联

用前一级计数器的输出作为后一级计数器的时钟信号。
实际上后级计数器的时钟信号可取自前一级的进位（或借位）输出，也可取自前一级计数器的高位触发器的输出。

同步级联

同步级联时，外加时钟信号同时接到各片的时钟输入端，用前一片的进位(或借位)输出信号作为下一片的工作状态控制信号（计数允许或使能信号）
只有当进位(借位)信号有效时，时钟输入才能对后级计数器起作用

两种方法：
(1)利用T端串行级联，各片的T端与相邻低位片的O_c相连

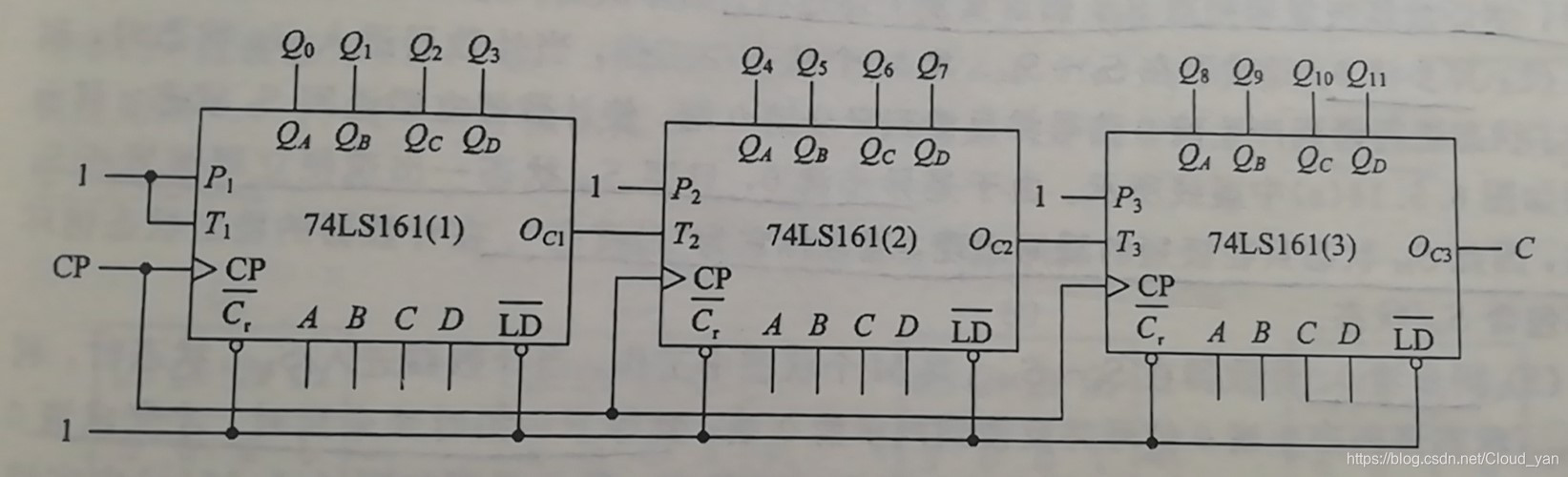
这种级联方式的工作速度较低，因为片间进位信号O_c是逐级传递的。

计数的最高频率将受片数的限制，片数越多，计数频率越低。

(2)利用P、T双重控制，最低位片的O_c并行接到其他各片的P端，只有T2不与O_c1相连，其他高位片的T端均与相邻低位片的O_c相连。