从0开始学习R语言--Day59--GAM模型

在分析数据前，我们通常会打印出数据的分布来观察其大致属于哪种分布，但其实除了一些很明显的回归或函数性质之外，我们很难单从数据分布定下用哪种回归，再加上传统意义上的神经网络的计算量相比普通的回归方法来说计算量很大，如果数据量很大的话，需要等待很多时间。

而相比之下，GAM模型就能过很好的适应这种情况，因为预先打印出数据的分布意味着我们知道函数式子的大致构成形式，缺少的可能是某些偏差或截距项，但通过知道函数在哪些地方有拐点。

以下是一个例子：

# 加载必要的包
library(mgcv)  # 用于GAM建模
library(ggplot2)  # 用于数据可视化

# 1. 生成模拟数据集
set.seed(123)
n <- 200  # 样本量

# 生成自变量
x1 <- runif(n, 0, 1)  # 均匀分布变量
x2 <- runif(n, 0, 1)  # 另一个均匀分布变量

# 生成非线性关系
f1 <- function(x) sin(2 * pi * x)  # 正弦关系
f2 <- function(x) exp(3 * x) / 10  # 指数关系

# 生成因变量(添加一些噪声)
y <- 2 + f1(x1) + f2(x2) + rnorm(n, 0, 0.2)

# 创建数据框
data <- data.frame(y = y, x1 = x1, x2 = x2)

# 查看前几行数据
head(data)

# 2. 可视化原始数据关系
ggplot(data, aes(x = x1, y = y)) + 
  geom_point() + 
  ggtitle("x1与y的关系")

ggplot(data, aes(x = x2, y = y)) + 
  geom_point() + 
  ggtitle("x2与y的关系")

# 3. 构建GAM模型
# 使用mgcv包的gam函数
# s()表示平滑项，bs="cr"表示使用三次回归样条(默认)
gam_model <- gam(y ~ s(x1) + s(x2), data = data)

# 查看模型摘要
summary(gam_model)

# 4. 模型诊断
# 检查残差
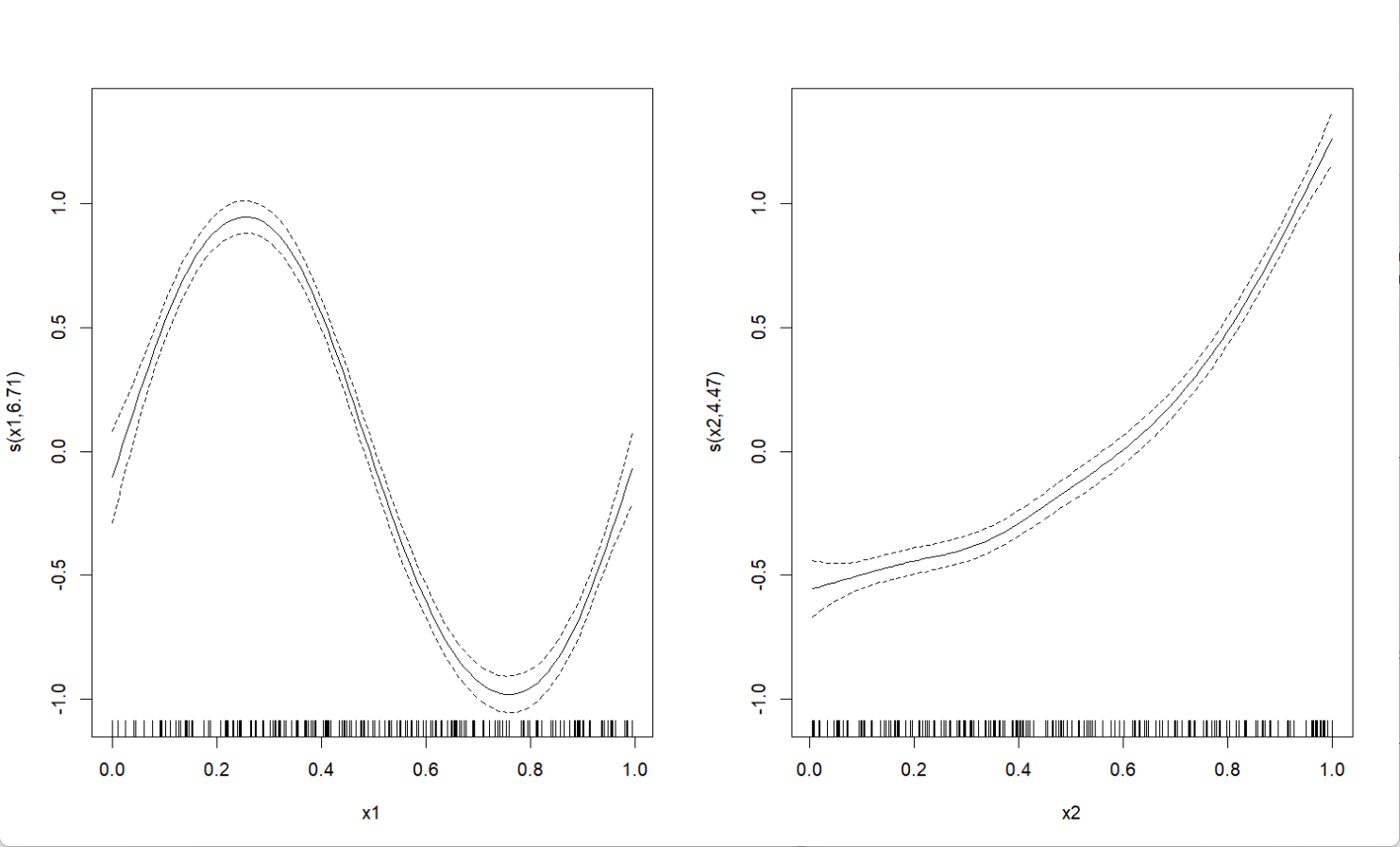
plot(gam_model, residuals = TRUE, pch = 1, cex = 1)

# 5. 可视化拟合结果
# 绘制各变量的平滑效应
plot(gam_model, pages = 1)

# 6. 预测新数据
new_data <- data.frame(x1 = seq(0, 1, length.out = 100),
                       x2 = seq(0, 1, length.out = 100))
predictions <- predict(gam_model, newdata = new_data, se.fit = TRUE)

# 将预测结果添加到新数据中
new_data$pred <- predictions$fit
new_data$se <- predictions$se.fit

# 可视化预测结果
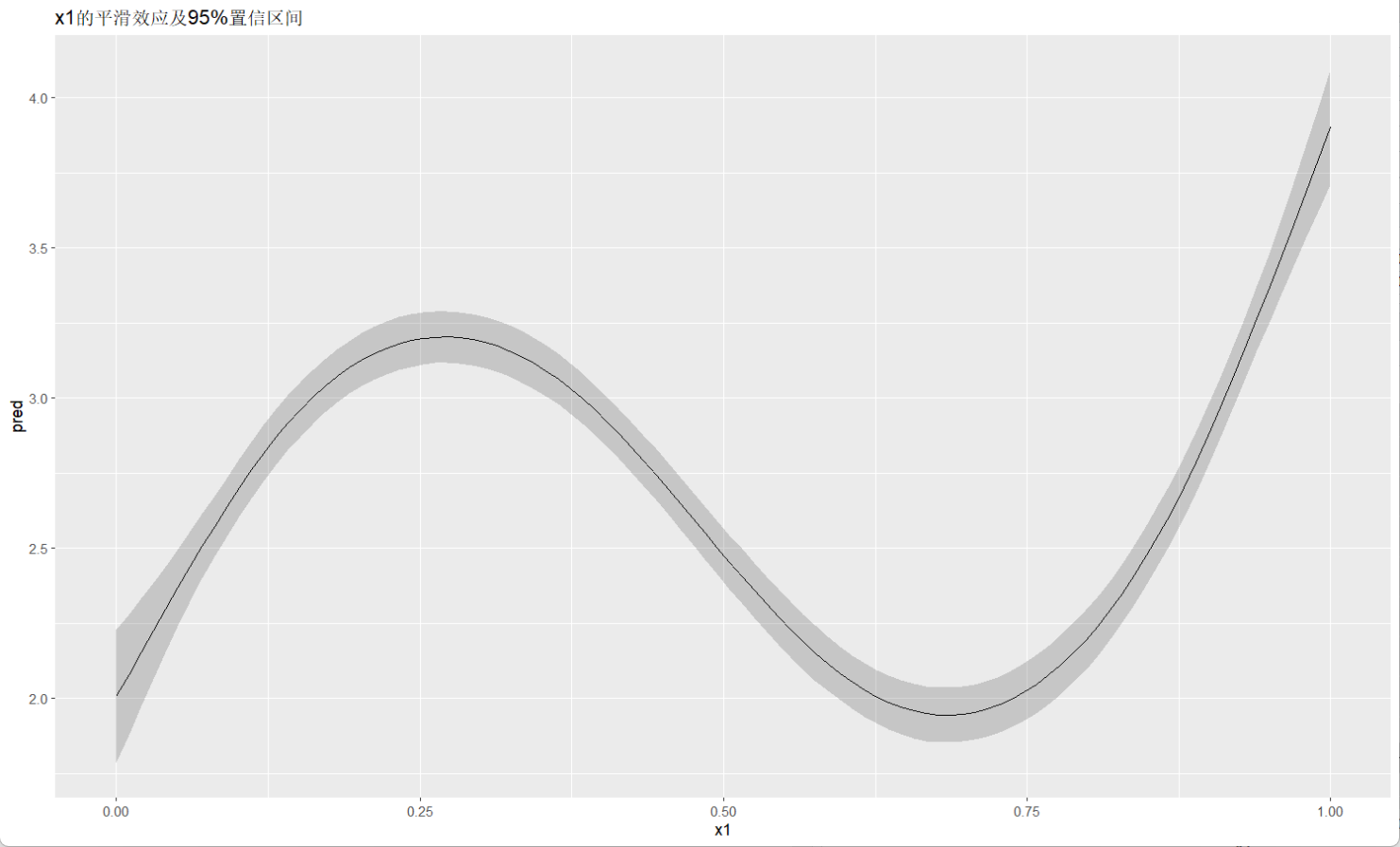
ggplot(new_data, aes(x = x1, y = pred)) +
  geom_line() +
  geom_ribbon(aes(ymin = pred - 1.96*se, ymax = pred + 1.96*se), alpha = 0.2) +
  ggtitle("x1的平滑效应及95%置信区间")

ggplot(new_data, aes(x = x2, y = pred)) +
  geom_line() +
  geom_ribbon(aes(ymin = pred - 1.96*se, ymax = pred + 1.96*se), alpha = 0.2) +
  ggtitle("x2的平滑效应及95%置信区间")

输出：