虽然我们常常在数据处理中做数据分布以及异常值的处理,但实际上对于缺失值,很多时候我们都不能简单地去删除或赋予0值,毕竟很多都是有意义的数据,只是可能因为各种原因没有在数据面板中显示,直接删除或赋予0这种忽略数据本身意义的做法,会破坏数据的属性,扭曲数据的性质。
一般来说,对于各种缺失的数据,我们都会用EM插补法来填补数据,原理是根据缺失所属的数据列,粗略估计一个数据后,计算等于这个值的概率,然后重复这个过程指到数值不再发生变化,简单来说就是根据已有的数据列参考来回归一个数据。
以下是一个例子:
# 加载必要的包
install.packages('mice',type = 'binary')
library(mice) # 提供EM插补功能
library(mvtnorm) # 用于生成多元正态分布数据
library(norm) # 提供EM算法实现
# 1. 生成模拟数据集
set.seed(123)
n <- 200 # 样本量
p <- 5 # 变量数
# 生成完整的多元正态分布数据
mu <- c(5, 10, 15, 20, 25) # 均值向量
sigma <- matrix(c( # 协方差矩阵
4, 2, 1, 0.5, 0.1,
2, 9, 3, 1, 0.5,
1, 3, 16, 4, 1,
0.5, 1, 4, 25, 5,
0.1, 0.5, 1, 5, 36
), ncol = p)
complete_data <- rmvnorm(n, mean = mu, sigma = sigma)
colnames(complete_data) <- paste0("X", 1:p)
# 2. 人为制造缺失值 (MCAR机制)
missing_data <- complete_data
for (j in 1:p) {
# 每个变量随机缺失20%
missing_indices <- sample(1:n, size = n * 0.2)
missing_data[missing_indices, j] <- NA
}
# 查看缺失模式
summary(missing_data)
md.pattern(missing_data)
# 3. 使用norm包进行EM插补
# 首先需要对数据进行预处理
s <- prelim.norm(missing_data) # 预处理
thetahat <- em.norm(s) # EM算法估计参数
# 获取插补后的数据集
em_imputed <- imp.norm(s, thetahat, missing_data)
# 查看插补后的完整数据集
head(em_imputed)
# 4. 使用mice包进行EM插补 (更简单的方法)
em_mice <- mice(missing_data, method = "norm", m = 1, maxit = 50)
complete_mice <- complete(em_mice)
# 比较原始数据和插补数据
par(mfrow = c(2, 3))
for (i in 1:p) {
plot(density(complete_data[, i], na.rm = TRUE),
main = paste("X", i), col = "blue")
lines(density(complete_mice[, i], na.rm = TRUE), col = "red")
legend("topright", legend = c("Original", "Imputed"),
col = c("blue", "red"), lty = 1)
}
# 5. 评估插补质量
# 计算均方误差 (仅对缺失部分)
mse <- numeric(p)
for (i in 1:p) {
missing_ind <- is.na(missing_data[, i])
mse[i] <- mean((complete_data[missing_ind, i] - complete_mice[missing_ind, i])^2)
}
print(paste("MSE for each variable:", paste(round(mse, 3), collapse = ", ")))
输出:
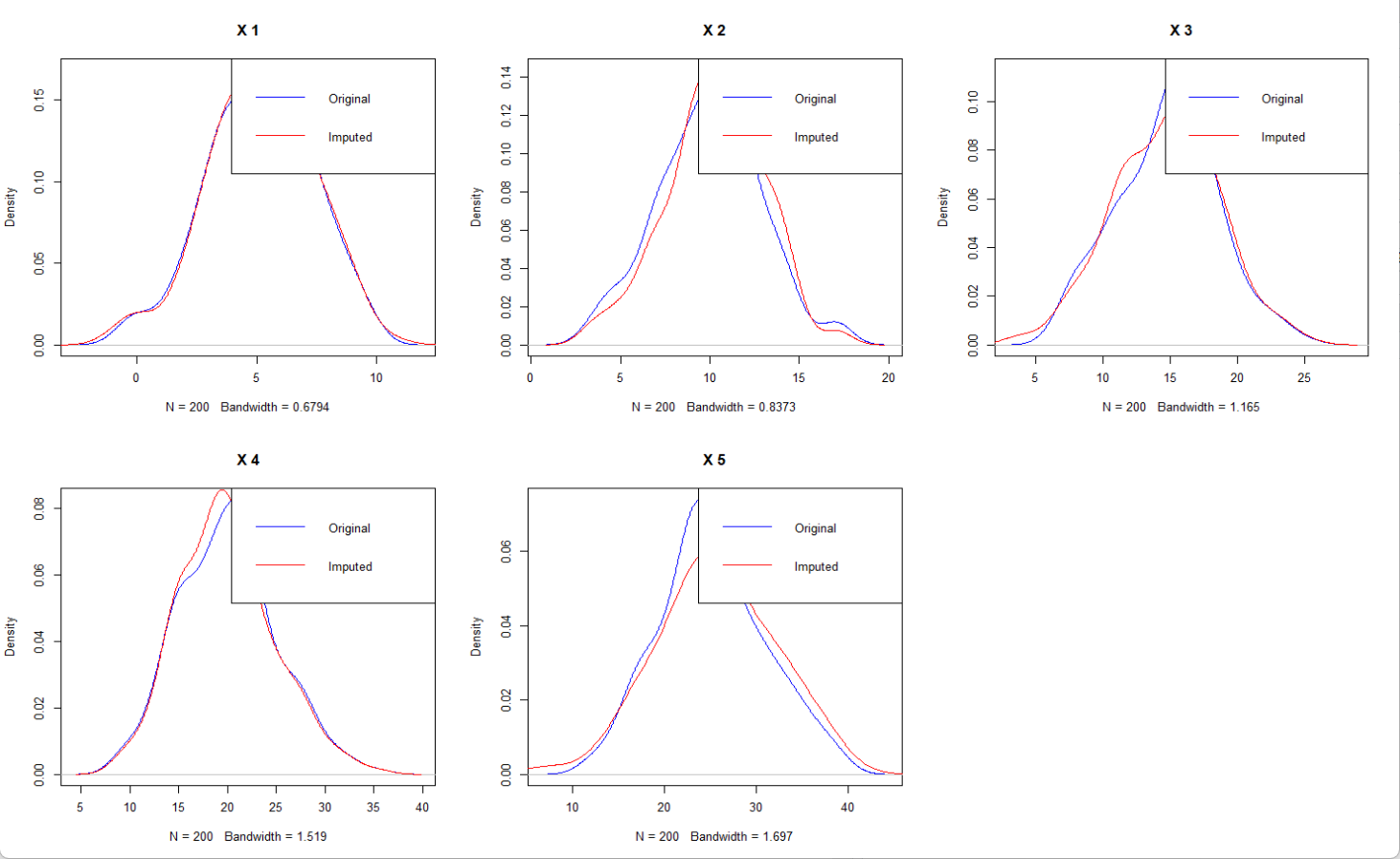
从整体来看,插补前后的曲线重合的地方很多,表明能够较好地修复数据,尤其是插补后没有看到有新的峰值或极端值。注意,如果缺失的值是一整年,同年份没有参考数据的话,就不能用EM,这种情况下的插补本质是一种预测了,要用函数的方法来做。
 R语言:EM插补法处理数据缺失值
R语言:EM插补法处理数据缺失值





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








