从0开始学习R语言--Day58--竞争风险模型

在用传统生存分析方法的场景中（如Kaplan-Meier和Cox回归），假设所有事件都是独立且互斥的，但在现实中，研究对象可能面临多种互斥的终点事件（如癌症患者可能死于癌症本身，也可能死于其他原因），如果直接去分析，模型会把这种结局时间错误地纳入评估，从而提高了病症的分析。

而竞争风险模型可以在考虑其他竞争风险存在的情况下，排除干扰求得某特定事件发生的概率。

以下是一个例子：

library(cmprsk)
library(survival)

# 生成模拟数据
set.seed(123)
n <- 200
data <- data.frame(
  age = rnorm(n, 60, 10),
  sex = factor(sample(c("Male", "Female"), n, replace = TRUE)),
  treatment = factor(sample(c("A", "B"), n, replace = TRUE)),
  time = rexp(n, 0.1),
  status = sample(0:2, n, replace = TRUE, prob = c(0.2, 0.4, 0.4))  # 0=删失, 1=主要事件, 2=竞争事件
)

# 准备设计矩阵
cov_matrix <- model.matrix(~ age + sex + treatment, data = data)[, -1]

# 拟合Fine-Gray模型
fg_model <- crr(
  ftime = data$time,
  fstatus = data$status,
  cov1 = cov_matrix,
  failcode = 1,  # 目标事件（如癌症死亡）
  cencode = 0    # 删失编码
  

)

# 提取基线累积风险（需要手动计算）
times <- sort(unique(data$time[data$status == 1]))  # 目标事件发生时间
base_cif <- cuminc(
  ftime = data$time,    # 事件时间
  fstatus = data$status, # 事件状态
  cencode = 0           # 删失数据的编码值（必须与数据一致）
)

# 提取基线CIF（仅目标事件）
cif_est <- base_cif$`1 1`$est
time_points <- base_cif$`1 1`$time

# 绘制基线CIF
plot(time_points, cif_est, type = "s", col = "red", 
     xlab = "Time", ylab = "Cumulative Incidence", 
     main = "Baseline CIF for Primary Event")

# 定义新个体（如：60岁男性，接受治疗A）
data$sex <- factor(data$sex, levels = c("Male", "Female"))
data$treatment <- factor(data$treatment, levels = c("A", "B"))
new_data <- data.frame(
  age = 60,
  sex = factor("Male", levels = levels(data$sex)),  # 继承原始水平
  treatment = factor("A", levels = levels(data$treatment))
)

# 现在可以安全生成设计矩阵
new_cov <- model.matrix(~ age + sex + treatment, data = new_data)[, -1]

# 计算线性预测值（LP）
lp <- sum(fg_model$coef * new_cov)

# 计算调整后的CIF
adjusted_cif <- 1 - (1 - cif_est)^exp(lp)

# 绘制预测CIF
plot(time_points, adjusted_cif, type = "s", col = "blue",
     xlab = "Time", ylab = "Adjusted CIF",
     main = "Predicted CIF for New Individual")
lines(time_points, cif_est, type = "s", col = "red", lty = 2)
legend("bottomright", c("Adjusted CIF", "Baseline CIF"), col = c("blue", "red"), lty = 1:2)

输出：

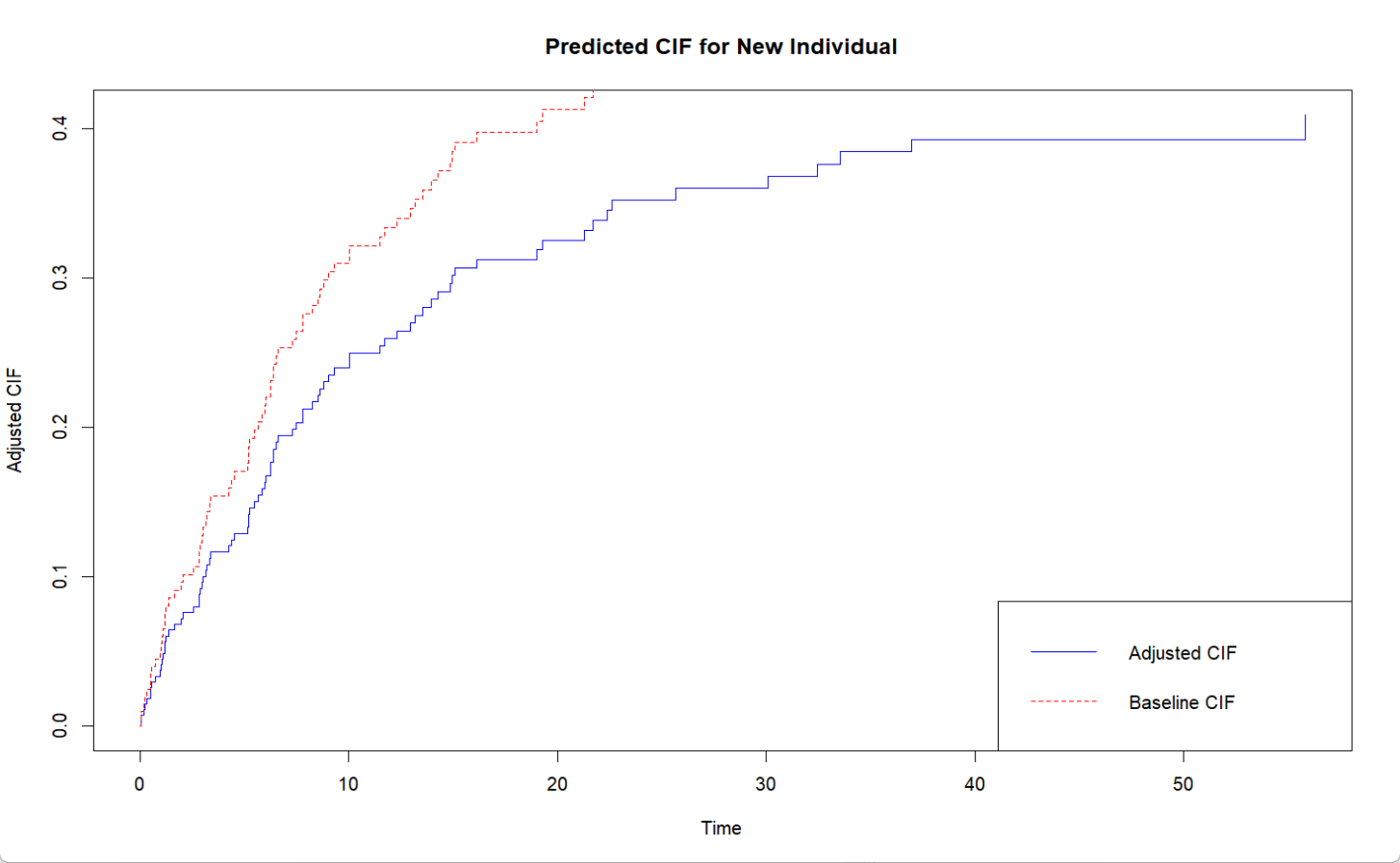
输出表明，新个体的累积发生概率在整个随访期内均低于基线水平，这表明其风险较低，且这种优势随时间推移更加明显，为个体化风险评估和精准干预提供了有力的量化依据。