【最近公共祖先】ST表法

模板题目：https://www.luogu.com.cn/problem/P3379

1 解题思路

求最近公共祖先，我们可以先用一个表f存储每个节点再跳1到若干跳可以到达的节点，另外我们用一个dep数组存储节点所处的深度（根节点的深度为1，这个用dfs去实现）。当一个询问来临，求点u和点v的最近公共祖先（假设u的深度大于v的深度），我们先让u来到和v同一深度的位置。之后看一下，如果来到同一深度时，两节点在同一位置，说明最近公共祖先是v。否则，就同时让u和v一起调到离最近公共祖先还差一步的深度，之后加一步就到最近公共祖先了。

2 进一步优化

洛谷的题目中提到：对于100%的数据，1≤N,M≤5×10^5。如果表f存的是各点每一跳能到达的节点，那么这样需要的空间很大，而且还会很浪费空间，因此，我们可以考虑使用ST表优化。
在这里，借用董晓老师的例子来说

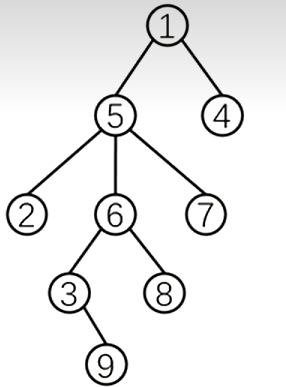
图中有9个节点，用二维数组f存储下标的信息，f[6][2]表示节点6跳两跳到达的节点。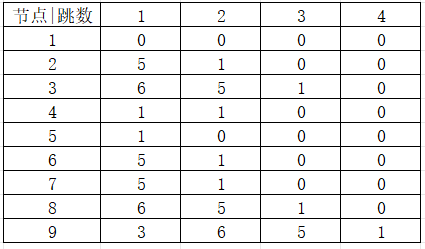
想象一下如果是一个9个节点的斜二叉树的话，那就会占用9×9的空间，并且会有很多的0出现，比较浪费空间。因此我们可以使用ST表来实现。下标如果用二维数组f来存数据，f[3][2]表示节点3跳2的2次方（即跳4跳）跳后到达的节点，因为跳4跳已经超出根节点了，所以用0存储。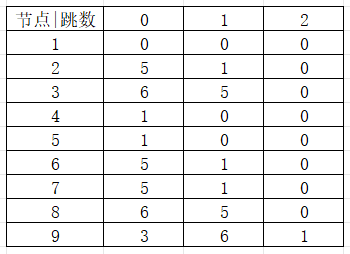
如果我们想知道节点3跳3跳到达的节点怎么求呢？我们不妨把3拆分成2+1（二进制拆分），先让3跳2跳到达节点5，在看节点5跳1跳，即看f[5][0]到达的节点是1。
使用ST表存储可以把表格的列数大大减少，如果用N个节点，那么最多需要1+log2(N)列。在填表的时候，我们遵循从上到下从左到右的方向去填，先填f[1][0]到f[N][0],再填f[1][1]到f[N][1],…,最后填f[1][log2(N)+1]到f[N][log2(N)+1]。

3 变量及数组说明

1. dep数组：存储节点的深度，根节点深度为1。
2. f数组：存储ST表信息。
3. 边使用链式前向星存储：
   ① head 数组：存储节点的一条出边
   ② to 数组：存储边的终点信息
   ③ nt 数组：存储要遍历的下一条边编号（一般来说，当前边和下一条边的起点是一样的）
4. lg2数组：主要用于对层树做二进制拆分
5. maxd：存储树的最大深度

4 AC代码

参考洛谷题解的代码：

#include<bits/stdc++.h>
using namespace std;
const int N=500005,M=N;
int n,m,s,lg2[N],f[N][22],head[N],ct,dep[N],maxd=-1; 
struct edge{
	int to,nxt;
}a[N<<2];
void add(int u,int v){
	a[++ct].to=v;
	a[ct].nxt=head[u];
	head[u]=ct;
}
void dfs(int x,int fa){
	f[x][0]=fa;
	dep[x]=dep[fa]+1;
	if(dep[x]>maxd) maxd=dep[x];
	for(int i=head[x];i;i=a[i].nxt){
		int tod=a[i].to;
		if(tod!=fa) dfs(tod,x);
	}
}
int lca(int u,int v){
	if(dep[u]<dep[v]) swap(u,v);
	// 先让u和v处于同一深度，深度差做二进制拆分
	while(dep[u]>dep[v]){
		u=f[u][lg2[dep[u]-dep[v]]];
	}
	if(u==v) return v;
	// 处于同一深度后，也是用二进制拆分，去让u和v再走一步祖先就相同。
	for(int i=lg2[dep[u]-1];i>=0;i--){
		if(f[u][i]!=f[v][i]){
			u=f[u][i],v=f[v][i];
		}
	}
	return f[u][0];
}
int main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=2;i<=n;i++) lg2[i]=lg2[i/2]+1; //深度不会超过n，所以记录到n就可以了
	for(int i=1;i<n;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		//这里要双向加边，便于dfs搜索，u和v谁是祖先要根据根节点dfs后来确定。
		add(u,v); add(v,u);
	}
	dfs(s,0);
	// 填ST表，要注意方向。具体要多少列，可以根据dfs之后的最大深度来定。
	for(int j=1;j<=lg2[maxd];j++){
		for(int i=1;i<=n;i++) f[i][j]=f[f[i][j-1]][j-1];
	}
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		printf("%d\n",lca(u,v));
	}
    return 0;
}