（十一）Support Vector Machine 理论 (支持向量机SVM 上)

最新推荐文章于 2025-03-18 23:12:12 发布

JaysenLeo

最新推荐文章于 2025-03-18 23:12:12 发布

阅读量441

点赞数

CC 4.0 BY-SA版权

分类专栏： python机器学习 SVM Python机器学习文章标签：支持向量机

本文为博主原创文章，转载文章须附上文章来源与作者。

本文链接：https://blog.youkuaiyun.com/ChangerJJLee/article/details/80642276

支持向量机（SVM）是一种强大的机器学习算法，尤其在深度学习兴起前备受推崇。本文介绍了SVM的起源、目标和工作原理，包括如何寻找最大化边际的超平面。在二维和高维空间中，SVM通过非线性映射解决线性不可分问题，利用核方法降低计算复杂度。此外，文章还探讨了SVM的特性，如不易过拟合和依赖支持向量。最后，讨论了核函数的选择及其在不同场景的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

背景：

最早期是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出
目前的版本(soft margin)是由Corinna Cortes 和 Vapnik在1993年提出，并在1995年发表
深度学习（2012）出现之前，SVM被认为机器学习中近十几年来最成功，表现最好的算法

机器学习的一般框架：

获取一个数据集作为训练集 => 从训练集的每一个实例中提取特征向量 => 针对这些特征向量结合一定的算法（分类器：比如 Decision Tree，KNN）=>得到训练好的模型=>有新实例来的时候就可以用得到的模型来预测，对其进行分类

引子

假设获取到一个训练集，每个实例有 $x_1$ , $x_2$ 俩个特征，将其在二维坐标上呈现出来如下，假如现在有俩类实例，我们的目标是在二维的空间中找到一条线，来最好的区分这俩类实例

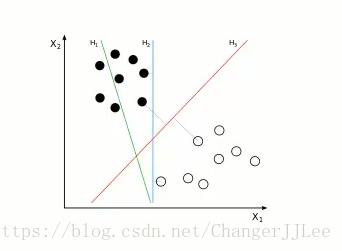
如上图一
扩展开，有n（n> 2）个特征向量的训练集，那么如上所要找的这条线变成了Hyperplane（超平面），即如何找到这样一个超平面最好（使边际margin最大，这也是为什么如上 $H_3$ 优于 $H_1$ ， $H_2$ 的原因，类似如下图）的划分俩类不同的点

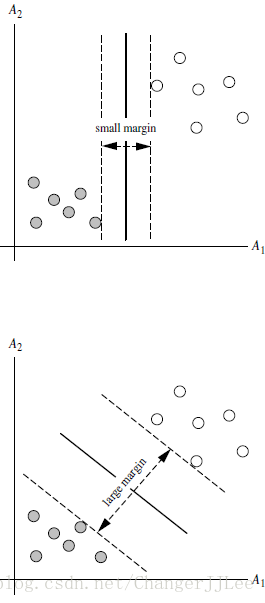
这里写图片描述

边际margin最大，也是为了利用这个所选的线,平面或者超平面能够在预测新的属性的时候犯错几率会减少

提出问题

总共可以有多少个可能的超平面？无数条
如何选取使边际(margin)最大的超平面 (Max Margin Hyperplane)？并且要求超平面到一侧最近点的距离等于到另一侧最近点的距离，两侧的两个超平面平行

介绍两个基本问题 线性可区分(linear separable) 和线性不可区分（linear inseparable)

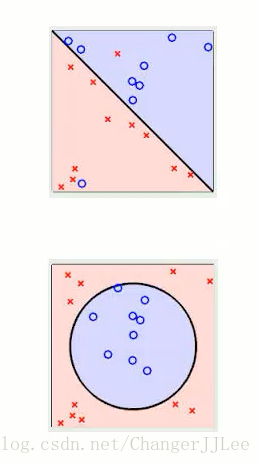
这里写图片描述

如上就是所谓的线性不可区分，而图一就是所谓的线性可区分

当实例是线性可区分(linear separable)的时候，我们如何建造SVM的超平面

从数学上将超平面定义成这样的公式

$W \cdot X + b = 0$ $W·X+b=0$
W是权重向量(weght vector)特征向量的个数也对应着了X的维度,n 是特征的个数，X是训练实例，b就是偏向bias
$W = {w 1, w 2, . . ., w n}$ $W= \{ w_1,w_2,...,w_n \}$

假设一个二维实例特征向量： X = （ $x_1, x_2$ ）,对于权重W也是个二维的（ $W_1, W_2$ ）,此时将b 也当做一个特征维度 $x_0其中(x_0 = 1)$ 的特征维度 $w_0$ ,此时超平面方程变为如下方程，即所有的点都在超平面上满足此方程：

w 0 + w 1 x 1 + w 2 x 2 = 0

$w_0+w_1x_1+w_2x_2= 0$

那么所有超平面右上方的点满足：
$w 0 + w 1 x 1 + w 2 x 2 > 0$ $w_0+w_1x_1+w_2x_2> 0$
那么所有超平面左上方的点满足：

$w 0 + w 1 x 1 + w 2 x 2 < 0$ $w_0+w_1x_1+w_2x_2< 0$
调整 weight , 使超平面定义边际的俩边定义公式如下，其中 $y_i$ 表示实例属于哪一类（class label），在这个问题中，只有俩类，-1，+1分别代表这俩类
当实例满足H1:w0+w1x