一文掌握电磁仿真算法知识

其实，这些电磁仿真软件无外乎就是求解设计体和空间的电磁场。这个电磁场的解就是我们要设计的结构。我们都知道，麦克斯韦方程组确定了电磁波的几乎所有，我们在结构内求解电磁场就可以了。

这看似简单，但面对这么多种材料，这么多的复杂的结构，又该如何求解呢？按照书本上讲的直接解电磁波方程就可以吗？很明显，不可以。

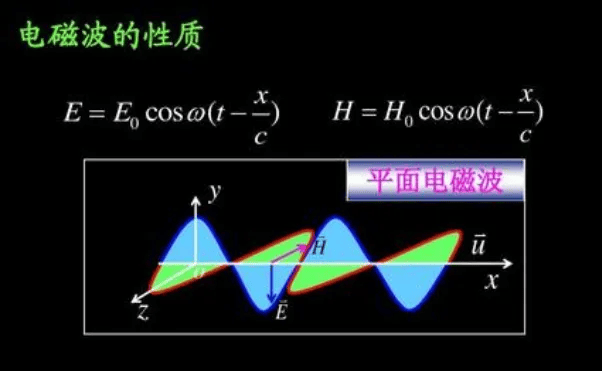
电磁学的一个很重要的分支，就是计算电磁学。

20世纪60年代以来，随着电子计算机技术的发展，一些电磁场的数值计算方法也迅速发展起来，并在实际工程问题中得到了广泛地应用，形成了计算电磁学研究领域，已成为现代电磁理论研究的主流。

简而言之，计算电磁学是在电磁场与微波技术学科中发展起来的，建立在电磁场理论基础上，以高性能计算机技术为工具，运用计算数学方法，专门解决复杂电磁场与微波工程问题的应用科学。

相对于经典电磁理论分析而言，应用计算电磁学来解决电磁学问题时，受边界约束大为减少，可以解决各种类型的复杂问题。原则上讲，从直流到光的宽广频率范围都属于该学科的研究范围。近几年来，电磁场工程在以电磁能量或信息的传输、转换过程为核心的强电与弱电领域中显示了重要作用。

电磁工程问题求解一般步骤如下：

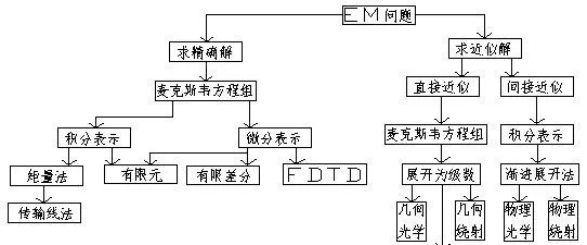
计算电磁学中有众多不同的算法，比如时域有限差分法（FDTD）、时域有限积分法（FITD）、有限元法（FE）、矩量法（MoM）、边界元法（BEM）、谱域法（SM）、传输线法（TLM）、模式匹配法（MM）、横向谐振法（TRM）、线方法（ML）和解析法等。

在频域，数值算法有：有限元法（FEM，Finite Element Method）、矩量法（MoM，Method of Moments），差分法（FDM，Finite Difference Methods）、边界元法（BEM，Boundary Element Method）和传输线法（TLM，Transmission-Line-matrix Method）。

在时域，数值算法有：时域有限差分法（FDTD，Finite Difference Time Domain ）和有限积分法（FIT，Finite Integration Technology）。

这些方法中有解析法、半解析法和数值方法。而数值方法中又分零阶、一阶、二阶和高阶方法。依照解析程度由低到高排列，其依次是：时域有限差分法（FDTD）、传输线法（TLM）、时域有限积分法（FITD）、有限元法（FEM）、矩量法（MoM）、线方法（ML）、边界元法（BEM）、谱域法（SM）、模式匹配法（MM）、横向谐振法（TRM）和解析法。

依照结果的准确度由高到低，其分别是解析法、半解析法、数值方法。

在数值方法中，按照结果的准确度有高到低，其分别是高阶、二阶、一阶和零阶。

时域有限差分法（FDTD）、时域有限积分法（FITD）、有限元法（FEM）、矩量法（MoM）、传输线法（TLM）、线方法（ML）是纯粹的数值方法；而边界元法（BEM）、谱域法（SM）、模式匹配法（MM）、横向谐振法（TRM）则均具有较高的分辨率。

模式匹配法（MM）是一个半解析法，倘若传输线的横向模式是准确可得的话。理论上，模式可以是连续谱。但由于数值求解精度的限制，通常要求横向模式是离散谱，这就要求横向结构上是无耗的。更通俗地讲，就是无耗波导结构。换言之，MM最适用于波导空腔、高Q且在能量传输的某一维上结构具有一定的均匀性。

比如，它适用于两个圆柱腔在高度维上的耦合的分析，但不适用于两个葫芦间的耦合分析。因为后者没有非常明确 的模式参与能量交换，人们只能将大量的模式一并考虑，这样就降低了MM的效用。

有限元法（FEM）是一种一阶纯数值方法（若用一阶元的话），它适用于任何形状的结构，是一个通用的方法。但事物总是一分为二的，一般来说，通用方法在特殊应用领域的效率将不如特殊方法。对于高Q空腔滤波器设计，MM就远优于FEM。

随着计算电磁学在工程应用领域影响力的不断加深，商用电磁分析软件越来越多，操作界面智能化，使得设计人员可以更加方便、直观得进行滤波器设计、天线设计、目标电磁特性分析等。

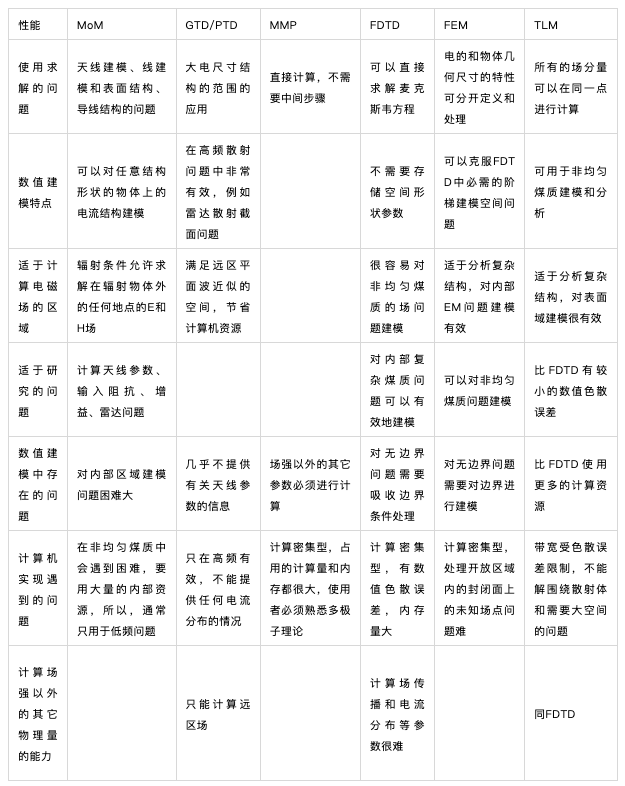
以下是几种方法的比较：

这里对计算电磁学中几种主要的数值方法进行简单的比较，即时域有限差分法（FDTD）、有限元（FEM）、矩量法（MoM）、多极子法（MMP）、几何光学绕射法（GTD）、物理光学绕射法（PTD）和传输线法（TLM）。