蓝桥杯2023（十四届）国赛——抓娃娃

抓娃娃（前缀和）

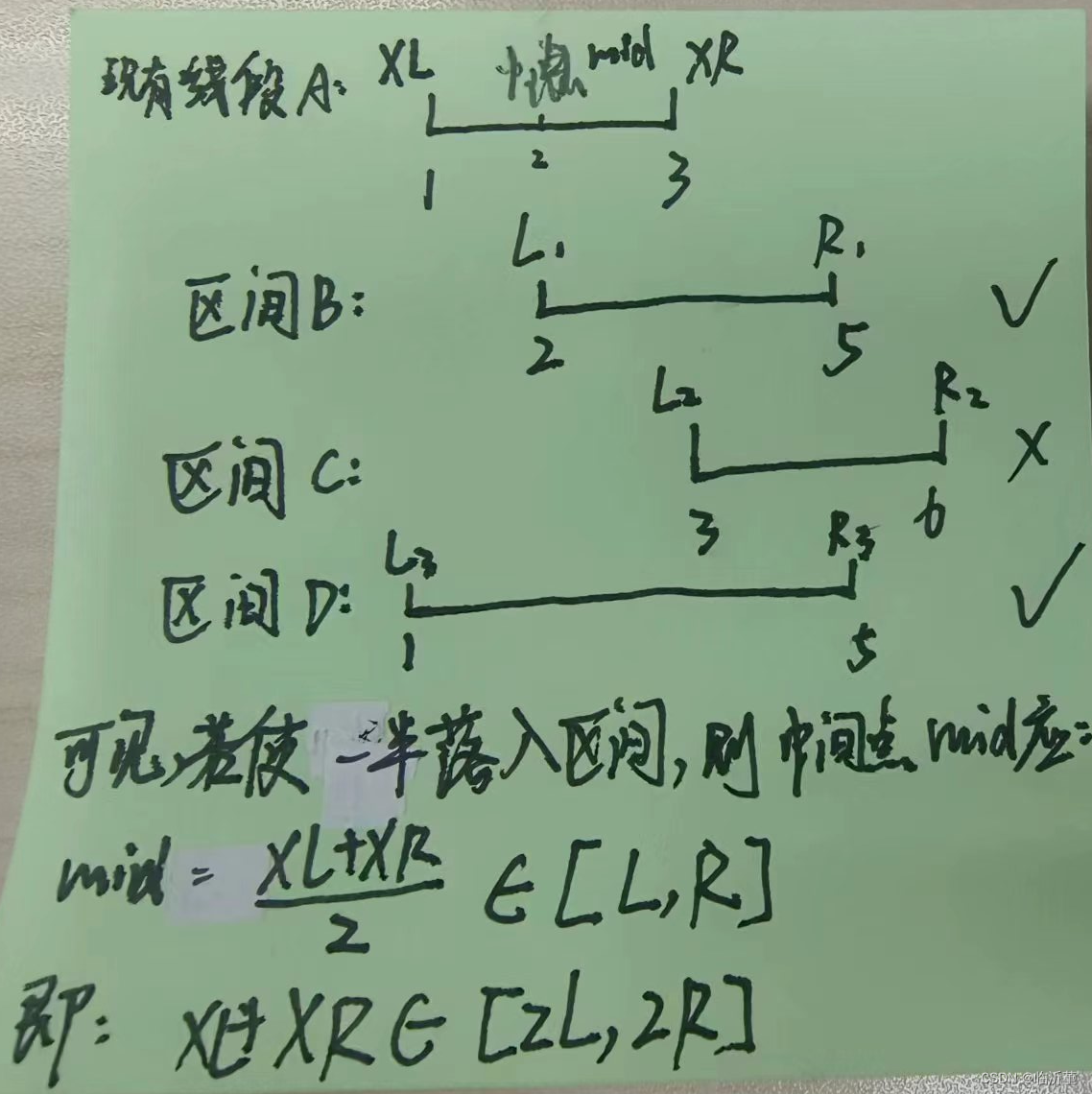
所以，我们使用线段两端点之和来代表该线段。最后只需要输出2L~2R这一段中存在的中点个数，即为总线段个数。

具体来说：

1. 当我们读取一个线段，例如 1~3，我们记录的是这个线段两个端点之和 1+3=4，在数组 a 的位置 4 处加一。

2. 接下来，我们计算前缀和数组 a。前缀和数组 a[i] 表示的是所有端点之和不大于 i 的线段的数量。

3. 对于查询区间 [L, R]，我们需要找出所有端点之和在 [2L, 2R] 范围内的线段。但由于我们只统计了端点之和，并没有直接统计线段的长度或位置，所以我们需要一个技巧来找出这些线段。

4. 考虑一个线段，其左端点为 xl，右端点为 xr。这个线段被区间 [L, R] 至少覆盖一半当且仅当 xl <= R 并且 xr >= L。但是，由于我们只统计了端点之和，所以我们不能直接检查这两个条件。

5. 但是，我们可以注意到，如果一个线段满足 xl <= R 并且 xr >= L，那么它的中点 mid = (xl + xr) / 2 一定满足 mid >= L 并且 mid <= R。因为线段被区间至少覆盖一半，所以中点一定在区间内或边界上。

6. 由于我们统计的是端点之和，而不是中点，我们需要将中点转换为端点之和。对于中点 mid，其对应的端点之和是 2 * mid。因此，我们要找的是所有端点之和在 [2L, 2R] 范围内的线段。

7. 最后，由于我们已经计算了前缀和数组 a，所以可以通过 a[2*R] - a[2*L-1] 来快速得到区间 [L, R] 内满足条件的线段数量。注意这里为什么是 2*L-1 而不是 2*L：因为我们需要包含左端点 L 对应的所有线段，而端点之和为 2*L 的线段并不包含在内（因为前缀和数组的下标是从 1 开始的）。

总结来说，虽然代码中没有直接处理线段长度或位置，但它通过统计端点之和并计算前缀和的方式，间接地实现了对线段和区间的处理。这种方法利用了线段中点与端点之和之间的关系，以及整数运算的便利性，来简化问题。

AC：

#include <iostream>
using namespace std;
const int N = 1e6 + 2;

int m, n;
int a[2*N] = { 0 };


int main()
{
	cin >> n >> m;
	int x, y;
	for (int i = 1; i <= n; i++)
	{
		cin >> x >> y;
		a[x + y]++;
	}
	
	for (int i = 1; i <= 2 * N - 1; i++)
		a[i] += a[i - 1];

	for (int i = 1; i <= m; i++)
	{
		cin >> x >> y;
		cout << a[2 * y] - a[2 * x - 1] << endl;
	}

	return 0;
}