【凸优化】使用PyTorch实现的初始点不可行的牛顿方法

【凸优化】使用PyTorch实现的初始点不可行的牛顿方法

本实验实现了初始点不可行的Newton方法。本实验使用Python作为编程语言，PyTorch作为机器学习库。

基本步骤

优化目标

$$\begin{gathered} \mathrm{minimize}f(x)=\frac{3}{2}{x}_1^2+\frac{1}{2}{x}_2^2-x_1{x}_2-2x_1 \\ \text{ s.t. }{x}_1+x_2=1 \end{gathered}$$
初始点
$$\begin{gathered} x^{(0)}=(0,0{)}^T \\ {v}^{(0)}=0 \end{gathered}$$

画图可知，这是一个凸函数。

代码

import torch


def f0_grad(x):  # 计算梯度
    y = f0(x)
    grad = torch.autograd.grad(y, x, retain_graph=True, create_graph=True)[0]
    return grad


def f0_Hessian(x):  # 计算Hessian矩阵
    y = torch.tensor([])
    for anygrad in f0_grad(x):
        y = torch.cat((y, torch.autograd.grad(anygrad, x, retain_graph=True)[0]), 1)
    return y


def f0(x):  # 计算目标值，改为你的待优化函数
    b = torch.tensor([-2., 0]).unsqueeze(1)
    A = torch.tensor([[3., -1], [-1, 1]])
    return 1 / 2 * x.t() @ A @ x + b.t() @ x


def main():
    A = torch.tensor([1., 1.], requires_grad=True).reshape(1, 2)
    b = torch.tensor([1.])
    x0 = torch.tensor([0., 0.], requires_grad=True).reshape(2, 1)
    v0 = torch.tensor([0.], requires_grad=True)

    alpha = torch.tensor([0.2])
    beta = torch.tensor([0.5])
    epsilon = 0.01
    x = x0
    v = v0

    def r(_x, _v):
        return torch.cat((f0_grad(_x) + A.t() @ _v, (A @ _x - b)), dim=0)

    count = 0
    while 1:
        # dim=0为上下拼接，dim=1为左右拼接
        # 计算两个值 Cx = d
        C1 = torch.cat((f0_Hessian(x), A.t()), dim=1)
        C2 = torch.zeros((1, 1))
        C3 = torch.cat((A, C2), dim=1)
        C = torch.cat((C1, C3), dim=0)
        d = torch.cat((f0_grad(x), A @ x - b), dim=0)

        solution = - C.inverse() @ d

        delta_x_nt = solution[0:2]
        delta_v_nt = solution[2]

        t = torch.tensor(1)

        while (torch.norm(r(x + t.mul(delta_x_nt), (v + t.mul(delta_v_nt)).reshape((1, 1))))) >= (
                1 - (alpha * t)[0] * torch.norm(r(x, v.reshape((1, 1))))):
            print(torch.norm(r(x + t.mul(delta_x_nt), (v + t.mul(delta_v_nt)).reshape((1, 1)))))
            print((1 - (alpha * t)[0] * torch.norm(r(x, v.reshape((1, 1))))))
            t = beta.mul(t)
            print(t)

        x = x + t.mul(delta_x_nt)
        v = v + t.mul(delta_v_nt)

        count = count + 1
        print('iter' + str(count) + ' x = ' + str(x.tolist()) + ' | f(x) = ' + str(f0(x)[0][0].tolist()))

        if A @ x == b or torch.norm(r(x, v.reshape((1, 1)))) < epsilon:
            break


if __name__ == '__main__':
    main()

运行结果：

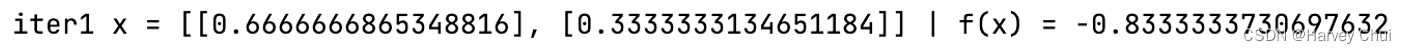
如果我的博客对你有帮助，欢迎点赞收藏
欢迎转载，转载请注明出处