力扣每日一题684.冗余连接1

 题目描述：

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

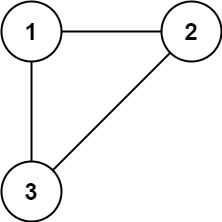
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

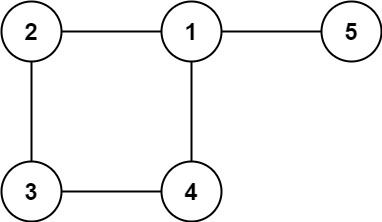
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

解题思路

1. 我们的目标是寻找冗余连接。冗余连接是指在无向图中，添加一条边后使得图形成环的那条边。
2. 该算法使用并查集（Union-Find）数据结构来检测环的存在。
3. t_Union 函数用于合并两个节点。首先找到两个节点的根节点。如果两个节点的根节点相同，说明它们已经在同一个集合中，形成了环，因此返回 false 并将这条边加入 ans。如果两个节点的根节点不同，根据树的深度决定如何合并：
   • 将深度较小的树合并到深度较大的树上。
   • 如果深度相同，则任意选择一个作为新的根，并增加其深度。

代码实现

class Solution {
public:
    vector<int> ans;
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        vector<int> parents(n + 1, -1);//存储每个节点的父节点
        vector<int> heigh(n + 1, 0);//存储根节点的深度
        for(auto edge : edges){//遍历所有的边
            if(!t_Union(edge[0], edge[1], parents, heigh)) break;
        }
        return ans;
    }
    int find_Root(int root, vector<int>& parents){//查找到根节点（祖先）
        while(parents[root] != -1){
            root = parents[root];
        }
        return root;
    }
    bool t_Union(int x, int y, vector<int>& parents, vector<int>& heigh){//合并
        int x_root = find_Root(x, parents);
        int y_root = find_Root(y, parents);
        if(x_root == y_root){//如果根节点相同，则存在环，合并失败
            ans.push_back(x);
            ans.push_back(y);
            return false;
        }else if(heigh[x_root] > heigh[y_root]){//将深度小的合并到深度大的根节点上
            parents[y_root] = x_root;
        }else if(heigh[x_root] < heigh[y_root]){
            parents[x_root] = y_root;
        }else{
            parents[y_root] = x_root;
            heigh[x_root]++;
        }
        return true;
    }
};