Diffusion Model扩散模型一文尽览！

作者 | 论文推土机 编辑 | 自动驾驶之心

 原文链接：https://zhuanlan.zhihu.com/p/1948137034842611877

点击下方卡片，关注“自动驾驶之心”公众号

戳我-> 领取自动驾驶近30个方向学习路线

>>自动驾驶前沿信息获取→自动驾驶之心知识星球

本文只做学术分享，如有侵权，联系删文

Diffusion 扩散模型整理

本文整理diffusion的数学原理，只有少量微分方程，随机微分方程和概率相关的公式，所以只需要基础数学背景也能完全看懂。如果实在看不懂也没关系，关注高亮块的结论即可。快速阅读办法就是只看高亮块然后接受结论即可。更快速的阅读办法是只看第一章朗之万采样建立对diffusion的直观印象即可。总结来说：相对论就是和美女在一起时间短，加班的时候时间长；diffusion就是用网络学习怎么解常微分/随机微分方程。

本文分成五部分内容：

1. 非常直观地介绍朗之万采样，并从diffusion和随机过程SDE开始建立diffusion在干什么

2. 然后介绍flow matching，which is modern technics

3. 统一两者框架

4. 介绍可控生成技术CFG

5. 探讨diffusion技术在planning中的应用

专业术语

首先我们整理与diffusion model相关的各个基础概念，这部分的整理都是数学定义，主要来自以下链接：

[An Introduction to Flow Matching and Diffusion Models]
arxiv.org/abs/2506.02070

总结来说就是我们使用velocity vector field来定义ODE(常微分方程)，因为微分可以类比为速度，方程所描述的场我们就称之为速度场。什么是VF(velocity vector field)的数学表达呢，我们用一条条的和起点以及时间相关的trajectory来描述VF，而flow就是这些trajectries的总和，称之为流。更多的数学定义就请看链接的第一章。

下面是数学定义，请直接跳过：

Langevin采样与DDPM

这部分的内容总结有一个非常好的视频讲解https://www.youtube.com/watch?v=Fk2I6pa6UeA。Diffusion model最重要的是diffusion，而不是model，diffusion基于随机过程，从一个分布到另一个分布的偏移，离散化表达下可以通过朗之万采样逼近，大数定理下等价连续表达。这个定理是diffusion model能够work的根本前提。本节介绍什么是朗之万采样，为什么他可以从一个分布迁移到另一个分布，diffusion model如何利用朗之万采样建模的，以及这个随机过程中的噪声对diffusion的生成任务有什么作用。

At the very beginning, please keep in mind that“扩散模型不仅是去噪器/变分自编码器（VAE）”。本质的观点是：图像生成=从一个高维概率分布里采样。难点在于“怎么从复杂的高维分布采样”。答案是借助朗之万采样（Langevin sampling），而扩散模型的神经网络负责去近似“分数函数”（score，亦即对数密度的梯度），用它来把随机噪声一步步“推向”高概率区域。
随机过程这条路线的关键结论是：只要知道分布的梯度（score）+ 加一点标准高斯噪声，就能采到目标分布的样本。 这既解释了扩散模型为什么好用，也解释了“为什么在生成过程中要一直加噪声”。

需要特别强调的是噪声并不是“副作用”，而是朗之万采样的“必需品”。
1，没有随机项，算法就退化为贪心地沿 ∇logp (log概率密度梯度)往上爬，容易卡在局部极大，样本多样性差；
2，加上噪声的随机扩散，才能既朝高密度前进，又能跳出糟糕区域，探索多模态；在图像里也可直观理解为“为高频细节提供原材料”，而网络负责把高方差的随机纹理整合成有意义的低方差结构。说白了，网络生成结构，噪声生成纹理。

朗之万采样

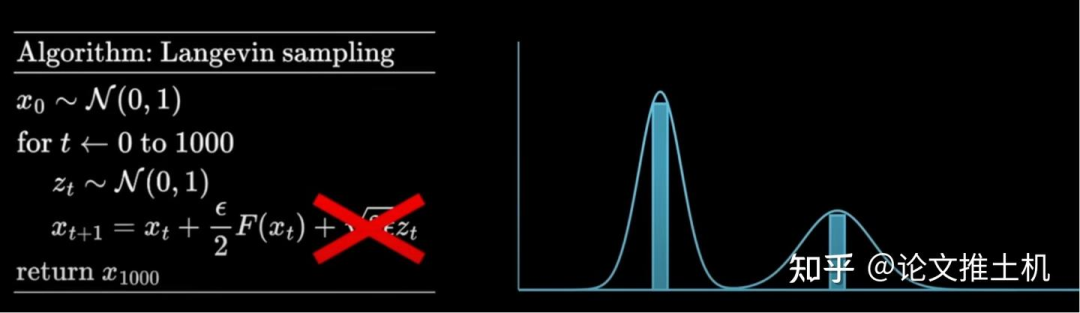
朗之万采样公式如下所示，这里的F(x_t)的F可以理解为物理学随机运动的potential field，对于概率角度的解释则是概率密度升高的方向：

首先我们来举一个最简单的例子，给定一个双峰高斯分布，通过不断的离散朗之万采样，我们可以获得图中的采样分布，随着采样次数不断上升，这个离散的蓝色离散采样将会无限逼近真实的双峰高斯分布。这就是随机过程的神奇之处。如果我们通过一个随机过程，能从任意的初始分布开始采样，然后就可以到达预先设定好的目标分布。同样的，我们假设我们知道了生成图像的分布（也就是数据分布），然后再用神经网络学习到这个F，我们就知道了从任意分布应该如何迁移，那不就可以完成diffusion的生成任务了吗。所以说diffusion model的生成任务，和掷骰子预测掷得得每个骰子面的概率任务毫无区别。

现在如果我们去掉朗之万采样的最后一个噪声项，会发现采样结果会非常不同，无论从什么起点开始采样，最后采样结果都会逼近与它最近的peak value，这是由于失去了噪声扰动造成的。这个结论很重要，因为diffusion同样需要噪声，否则也只会逼近peak value，而peak value在复杂的高维数据分布中，不一定代表有意义的生成结果。

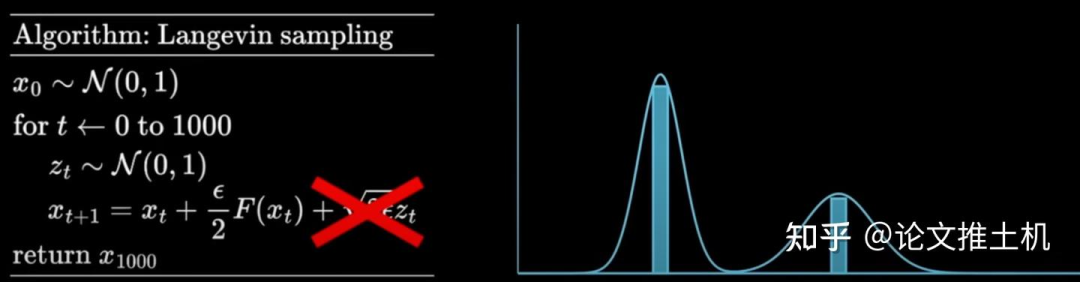
下面举一个例子，分别是不带噪声和带噪声的朗之万采样过程对高斯分布的拟合过程。不带噪声的过程必然会采样到目标分布的peak value，而带有噪声则会拟合到目标分布上，而不是永远拟合到peak value。

现在看来，这个朗之万采样中的F term非常关键，他的公式就是：

需要强调的是这里为什么是log prob 而不是直接prob，直接使用prob对于概率密度角度来说已经是完全足够了，但是为了让朗之万采样更加高效，我们采用log prob，上述推导中看得出这个分母起到了scalable step length的作用。远离peak value的时候step会变大，随着逼近peak value，step length则变小。

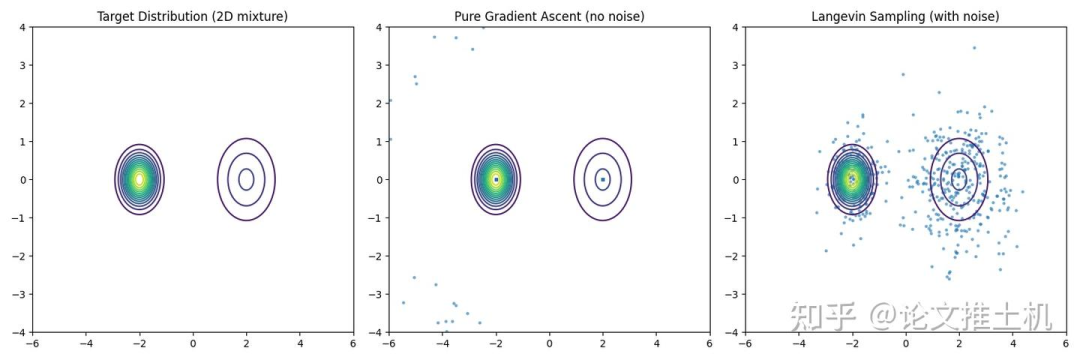
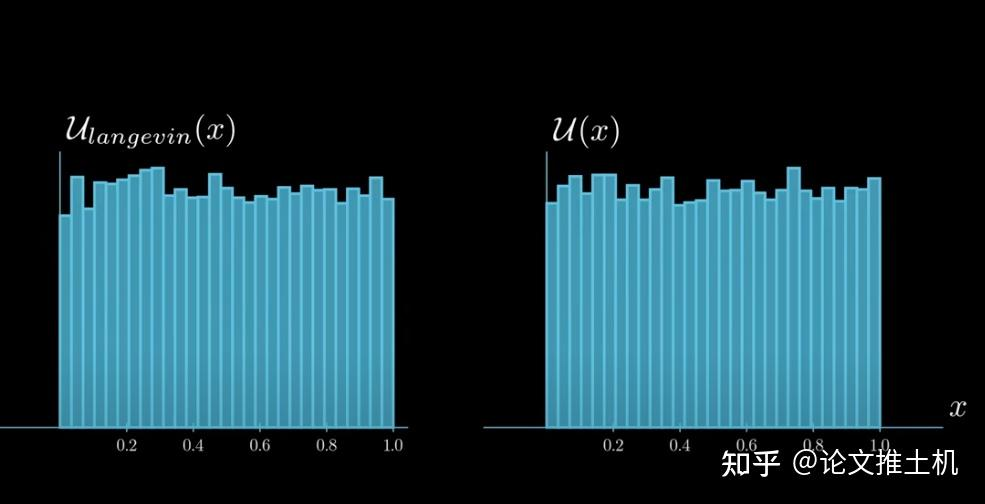
事实上，对于任何分布，都可以采用朗之万运动逼近，比如再举一个例子，对于掷骰子行为的分布是什么呢，是uniform 分布，掷骰子的任意面的概率都是1/6，所以我们可以先验地知道我们要拟合的分布是什么，然后计算出F term，然后模拟朗之万运动，左图是目标分布和朗之万的F term的表达，这里的表达方式可以用次梯度(sub-gradient)理解，右图是使用朗之万采样和直接使用uniform分布采样获得的结果，完全无法区分。

然后举一个更加一般性的例子，拟合一个双月分布：

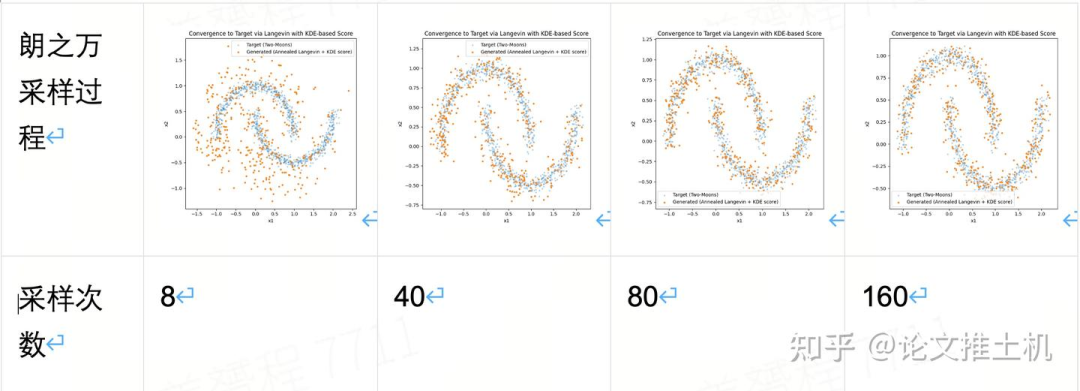
多维分布的可视化

以上内容展示了一个简单的uniform分布，以及一个简单的双峰高斯分布和双月分布下的朗之万采样过程。同样的，我们继续复杂化多维分布，可以通过可视化展示的多维分布最多到三维，如下图所以，就是各种不同的多维分布。其中的箭头和箭头长短表示了在各个采样点上的概率密度梯度函数，也就是上面朗之万采样公式中的F term：

现在我们把diffusion model的生成任务和朗之万运动采样过程结合起来，掷骰子任务的采样过程要计算每个掷得得面的概率，我们很容易知道这个分布是uniform，而生成一张图片，是否也可以有一个图片生成的概率分布，然后在这个分布上进行朗之万采样达到生成一张图片的目的呢，肯定是有的。diffusion model做的就是通过神经网络拟合出数据分布，然后在推理阶段sample出图片。

采样噪声

采样噪声对diffusion model至关重要。噪声并不是“副作用”，而是朗之万采样的“必需品”。网络负责提供“宏观形状、结构、方向”；噪声提供“高频细节（纹理、颗粒感、局部随机性）”。两者结合，才能合成真实感的图像。

如果没有噪声项：

迭代就是梯度上升，点会收敛到某个局部极大值（peak），即分布的模态（mode）。→ 结果是“模式搜索”，不是“采样”。你得到的只是峰值位置，而不是分布中的多样样本。

加上噪声项：

这个高斯噪声和梯度项结合起来，实际上是 一个随机微分方程 (SDE)。数学上可以证明：

• 其平稳分布 (stationary distribution) 就是目标分布 p(x)。

• 也就是说，随着迭代次数趋向无穷，采样轨迹不会只卡在峰上，而是会在整个分布上游走，长时间平均符合 p(x)。

首先我们给出一个实例来看采样噪声对采样过程会产生什么样的影响。在一个采样过程中，首先前500去噪过程是带着这个随机噪声的，然后500步以后去掉这个噪声term，发现前面的去噪过程生成小熊猫的形态虽然有噪声，但是结构更加清晰，反而是去掉噪声term之后，小熊猫的生成效果变得更差了。

之前我们强调过，去掉噪声term的朗之万采样过程失去了随机性，所以采样的结果会让采样点最终逼近peak value。

对于我们的数据分布，你以为是这样的，其实是这样的：

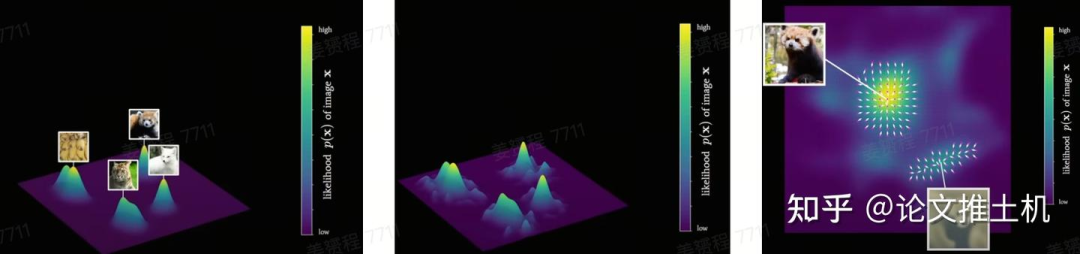
所以噪声项起到了类似于梯度下降中防止梯度落入局部最优的效果，让采样点逼近数据分布，但是一旦落入数据分布的局部最优点的时候还有机会跳出寻找更好的最优数据分布。可以理解为diffusion model起到了刻画生成的图片的结构的作用，而噪声则负责纹理生成。下面给出一个迭代优化的过程：

和GAN的对比

从上面可以看出一个生成网络既要习得creativity来确保生成的多样性，同时还要学到methodical capabilities来确保生成的东西的合理性。这两个优化loss是互相矛盾的，在GAN方法中，网络需要去分类在不同的layer更倾向于学习什么能力以及在这个方面体现多强的引导性。这就有可能产生一个模式坍塌的现象，网络倾向于生成类似的结果。而diffusion将多样性的任务给到噪声，一定程度上缓解了这个问题。

朗之万采样的潜在问题

要知道数据分布是稀疏的，并不是所有采样点都有梯度，所以朗之万采样的一个潜在问题就是采样效率。

高斯核平滑分布

训练目标分布是离散分布，我们需要使用一个方法将离散分布变成连续分布，然后才能求梯度，然后才能用神经网络去学习，而常用的连续化策略就是高斯和平滑，将离散分布和kernel density function（常用的就是Gaussian KDE）结合，描述连续分布。下面介绍KDE的平滑策略：

采用KDE得到训练目标

首先给出结论，常用的紧凑KDE score function表达是：

这个就是我们的训练目标，

下面是具体的推导：

训练目标

给出score matching伪代码：

# ---------------------------------------------
# Model & Schedules
# ---------------------------------------------
# s_theta(x, sigma): 神经网络，输入加噪样本 x 与噪声尺度 sigma，输出对 score 的估计。
# sigmas: 一串从大到小的噪声尺度（如对数等比递减），覆盖[σ_max, σ_min]。
# w(sigma): 不同噪声尺度的损失权重（实践中常与σ相关，避免大/小噪声主导）。

initialize params θ  # 随机初始化网络参数
define schedule sigmas = geomspace(σ_max, σ_min, T)  # 例如 T=100~1000
define weight w(sigma) = c * sigma**2  # 常见做法之一：按σ缩放损失，平衡梯度

# ---------------------------------------------
# Training Loop (Denoising Score Matching)
# ---------------------------------------------
for step in range(num_train_steps):
    # 1) 取一批真实样本
    x0_batch = sample_from_dataset(batch_size)

    # 2) 随机抽一个噪声尺度（或对每个样本独立抽）
    sigma = sample_uniform_in_log_space(σ_min, σ_max)

    # 3) 加噪得到“观测样本” x
    #    x = x0 + σ * ε,  ε ~ N(0, I)
    eps = standard_normal_like(x0_batch)
    x_noisy = x0_batch + sigma * eps

    # 4) 计算“真分数”的监督信号（由去噪等式得到）
    #    ∇_x log q_σ(x) = (E[x0|x] - x)/σ^2
    #    但我们不直接算 E[x0|x]，用“去噪等式的目标形式”：
    #    目标分数 = (x0 - x)/σ^2   （在 x=x0+σ ε 时，它与上式等价于 E step 的无偏目标）
    score_target = (x0_batch - x_noisy) / (sigma**2)

    # 5) 网络预测分数
    score_pred = s_theta(x_noisy, sigma)

    # 6) 损失：加权 MSE（或可选其他稳健损失）
    loss = mean_over_batch( w(sigma) * ||score_pred - score_target||^2 )

    # 7) 反向与优化
    θ = optimizer_step(θ, grad(loss, θ))

# 训练结束后，s_theta 学到在各噪声尺度的 score 近似
save_model(θ)

与之等价的另一种表达方式是学习噪声，两者完全等价，只是两种不同的表达方式，学习score等于学习噪声，公式中只是相差了一个系数，两者的关系就是s_theta(x_t, t) ≈ -(1/σ_t) * eps_theta(x_t, t)。其中s_theta是score function， eps_theta是noise。

下面给出伪代码：

# ---------------------------------------------
# Model & Schedules
# ---------------------------------------------
# eps_theta(x_t, t): 神经网络，输入 x_t 与时间步 t，输出对添加的噪声 ε 的估计。
# 这里使用常见的 VP/VE 调度（任选其一），需要能计算 α_t, σ_t 以生成 x_t。
initialize params θ
define {α_t, σ_t} for t in [1..T]  # 前向加噪调度，如线性/余弦/指数等

# ---------------------------------------------
# Training Loop (Predict Noise)
# ---------------------------------------------
for step in range(num_train_steps):
    x0_batch = sample_from_dataset(batch_size)
    t = sample_uniform_int(1, T)  # 随机选时间步

    eps = standard_normal_like(x0_batch)
    # 前向加噪： x_t = α_t * x0 + σ_t * ε
    x_t = α[t] * x0_batch + σ[t] * eps

    # 预测噪声
    eps_pred = eps_theta(x_t, t)

    # 损失：MSE(ε, ε_pred)，有时会有权重/预条件
    loss = mean_over_batch( ||eps_pred - eps||^2 )

    θ = optimizer_step(θ, grad(loss, θ))

# 训练结束后，eps_theta 学到 ε；与 score 的关系： 
#   s_theta(x_t, t) ≈ -(1/σ_t) * eps_theta(x_t, t)
save_model(θ)

两者整理可得：

这里给出了两种不同的加噪方式，分别是VE，VP，一个是variance exploding ：随着 t 增大，方差逐渐增大，最终变成高斯噪声。一个是virance preserving：数据和噪声混合，保持总方差不变。

然后我们给出这两个特殊形式的score function的close form solution：

比如我们以VE为例，它采用gaussian prob path，可以计算出close form score function，伪代码如下所示：

Flow matching

Flow matching的宏观分类如下图所示：

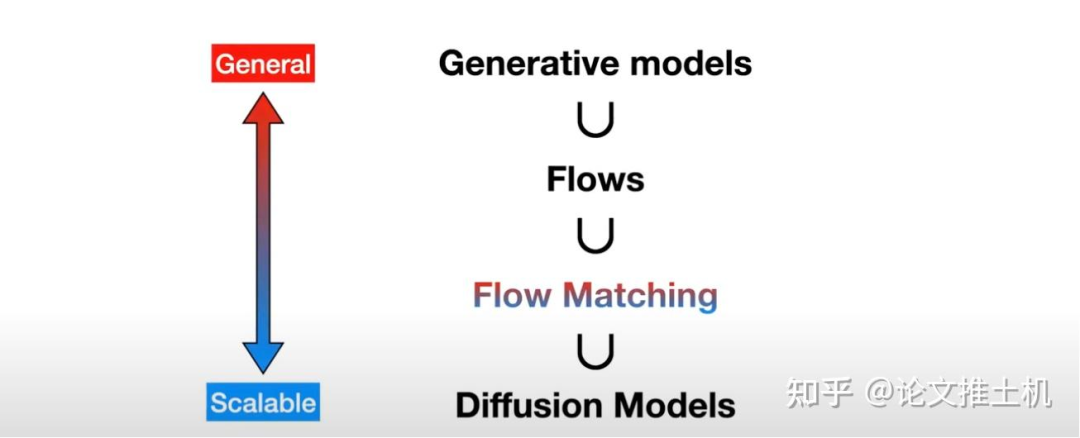
Flow matching的数学推导

推荐Flow matching作者，来自Meta的Yaron Lipman自己的讲解：https://www.youtube.com/watch?v=5ZSwYogAxYg

采用连续性方程推导cfm = fm，fm中有marginal term u(t),需要对conditional prob进行数据分布积分，这个是无法做到的，我们容易获得是conditional prob， u(t|x_t)。通过证明，我们可以知道两者等价，这样就可以构建cfm训练目标。

以上两者等价。

Flow Matching的伪代码，非常的简单。 只有五步：

1. Sample from t

2. Sample from data

3. Sample from noise

4. Compute u target

5. Compute gradient

最优传输CondOT

伪代码如下，这也是ReFlow中采用的采样策略：

具体证明可以看到An Introduction to Flow Matching and Diffusion Models中的4.1节flow model。这里有一个有意思的解释，flow matching中对于采样如果使用线性插值，从越高的维度观察这个流模型的速度方向，则越接近直线，这个结论同样适用于mean flow。下图来自On Kinetic Optimal Probability Paths for Generative Models

事实上，CondOT采样策略也是flow matching中最常用的采样策略，它采样又快又简单，推理也又快又简单，Lipman给出了一个checkboard例子：

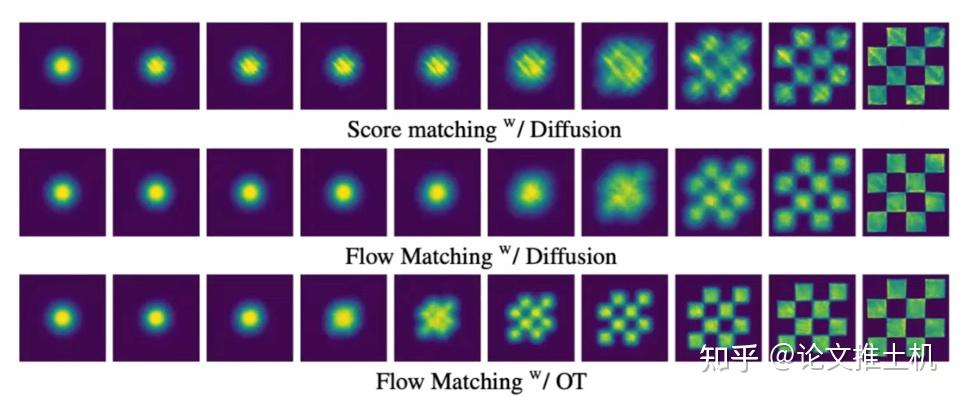
BatchOT

BatchOT在小批次中把噪声样本与数据样本配对，然后拿这些成对的样本进行瞬时速度场训练，其实已经在描述一种平均的概念，但是这个平均还是基于学习瞬时速度场的平均来说的。而meanflow的平均则是在学习平均速度场。

• batchOT（mini-batch Optimal Transport in CFM/RF）做的是：在每个小批里，用（近似）最优传输把噪声样本与数据样本配对，再在这些成对样本之间训练瞬时速度场（flow matching / rectified flow 的常规目标不变）。这么做等价于用更“合理”的耦合来逼近 Monge 映射/位移插值，使路径更直、训练方差更小、少步采样更稳。

• MeanFlow做的是：把监督从“瞬时速度 v(x,t)”换成区间平均速度（平均沿程速度），并利用一个“平均-瞬时速度恒等式”来训练，从而直接瞄准一歩生成（1-NFE）的映射；它本身不依赖 OT 来配对样本。

所以两者进行异同：
相似点：两者都在鼓励“端点对端点”的直线/低曲率传输，这有利于少步甚至一步采样。batchOT 通过“更好的配对”达到这个效果；MeanFlow 通过“更合适的监督信号”达到这个效果。

不同点：

• batchOT 是耦合策略（训练数据如何两两配），目标仍是 FM/RF 的瞬时速度回归；

• MeanFlow 是目标函数/表征的改变（学平均速度），直接服务于一步生成；

Toy example

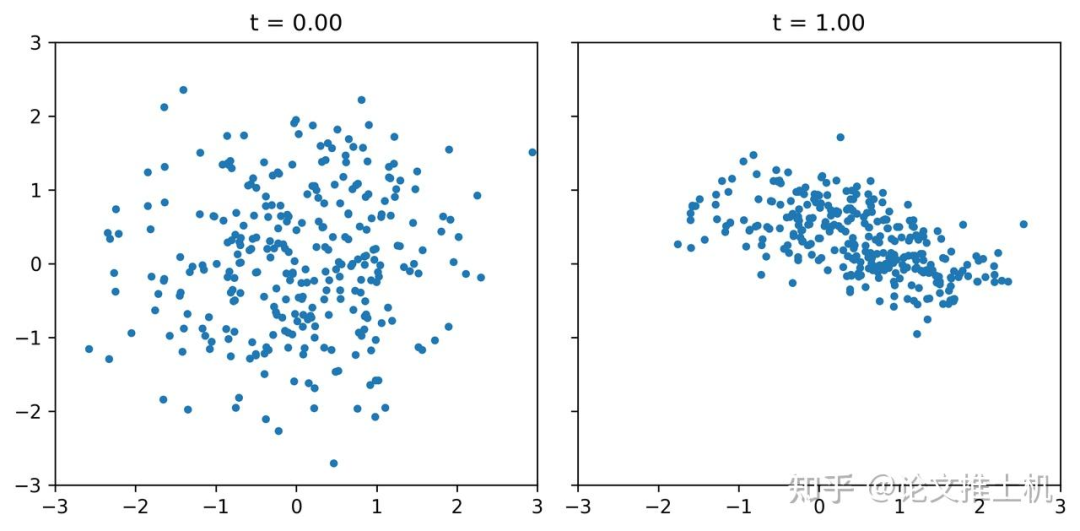
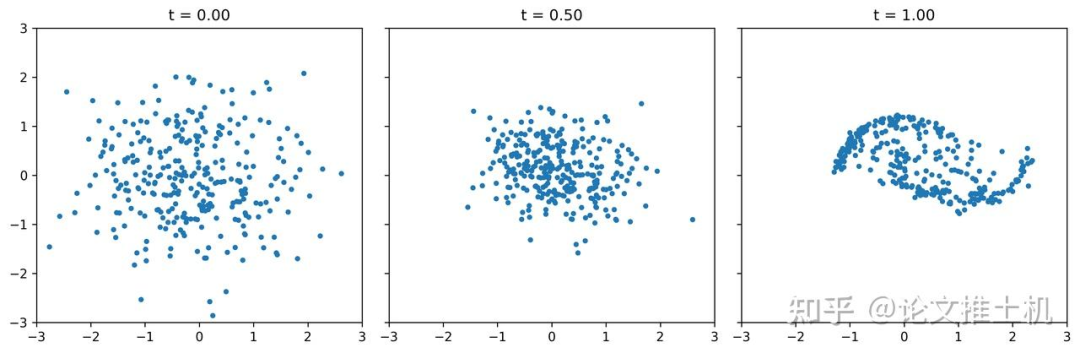
我们用https://github.com/facebookresearch/flow_matching/blob/main/examples/standalone_flow_matching.ipynb这个里面的flow matching exmaple对比常规训练的flow matching在推理阶段进行多步去噪和单步去噪的区别，事实上，从理论上来讲flow matching学习的是瞬时速度，在推理阶段必须使用多步去噪，前向欧拉多步去噪，如果使用单步去噪或少步去噪，效果就会大打折扣。toy example拟合的是双月模型，事实上真实任务的数据分布非线性程度更大，也就是说，就是是一个二维简单模型，我们都不可能使用瞬时速度流去进行few step去噪得到什么好结果。下面给出使用不同推理步数的去噪结果：

consistency models

TODO：介绍一致模型。

rectified flow (Liu et al., 2022)

• 官方提供的小例子：https://colab.research.google.com/drive/1CyUP5xbA3pjH55HDWOA8vRgk2EEyEl_P?usp=sharing#scrollTo=83Ezibj7_yyR

• 可视化理解：https://www.cs.utexas.edu/~lqiang/rectflow/html/intro.html?utm_source=chatgpt.com，https://rectifiedflow.github.io/blog/2024/intro/?utm_source=chatgpt.com

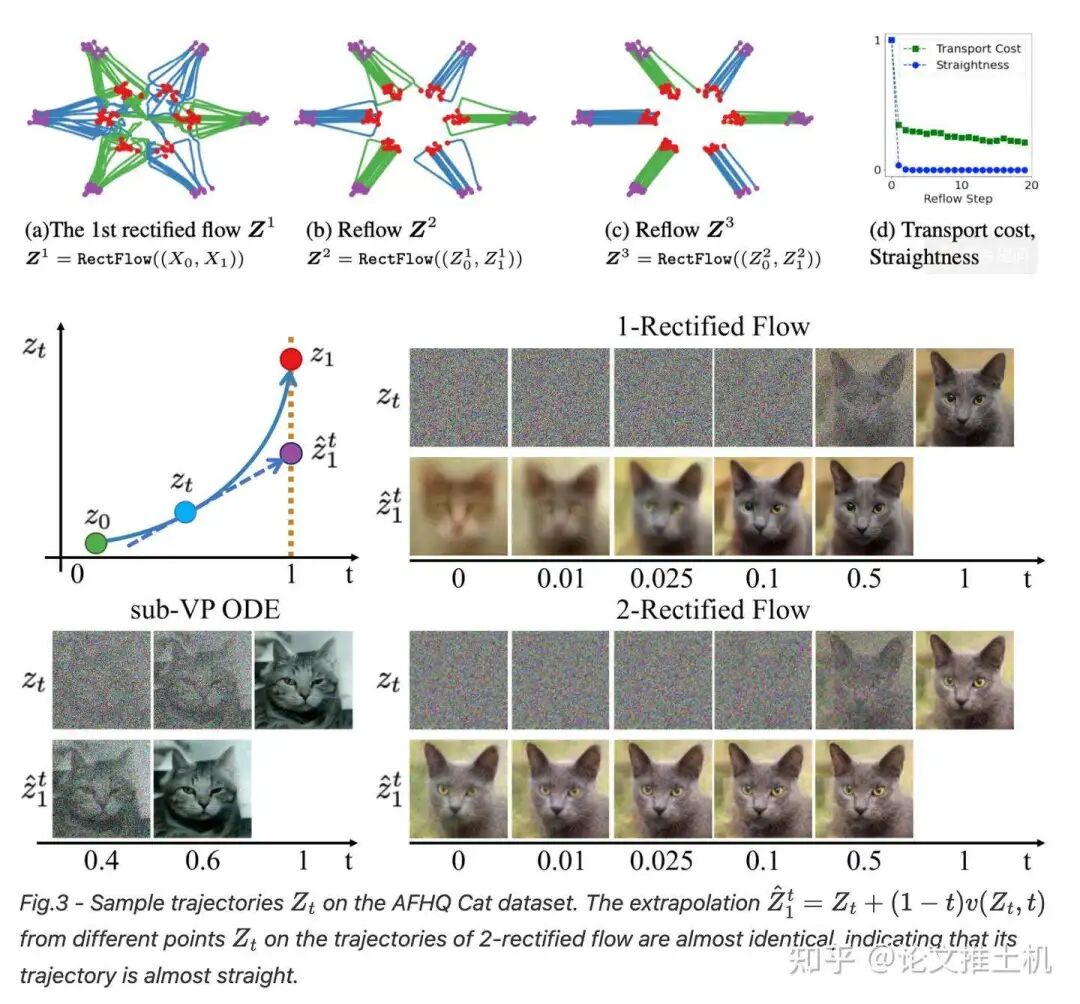
Reflow做了什么事情，就不多说了，直接看到原文：https://arxiv.org/pdf/2209.03003，让GPT进行总结：

这里面有一个很有意思的点就是reflow，一般理解就是通过类似于蒸馏的思路把多步去噪蒸馏到单步去噪，有点意思，单步去噪不就是Mean flow的想法吗。作者自己说了：

meaning that the ODE can be solved exactly with a single Euler step, which addresses the very bottleneck of slow inference of ODE/SDE models. Hence, this reflow/straightnening procedure provides a special way for training one-step generative models (such as GAN/VAE), by leveraging ODEs as an intermediate step. For practical image generation, we find that it is sufficient to only reflow once.

更深层次的理解，既然作者希望“this reflow/straightnening procedure provides a special way for training one-step”，希望学习到的速度流能够尽量拉直，其实和Meanflow的思路是一致的，meanflow希望在高维空间中找到直直的平均速度流，而这个reflow操作就是通过类似于不断蒸馏的方式，也在高维空间中使用瞬时速度场找到平均速度场，从而也可以实现一步去噪，这样瞬时速度场等价于平均速度场。

Mean flow

1. Mean flow属于flow matching家族，网络学习的是速度场，但有别于常规的flow matching技术（学习瞬时速度场），mean flow顾名思义学习的是平均速度场。Rectified flow也是flow matching家族的一员。reflow是mean flow的特例，在满足一定特别条件的时候（r = t）时，mean flow退化为rectified flow。所以mean flow的性能总是被rectified flow兜底。我们可以类比为端到端模型输出完全不可用时，总是可以被后处理兜底，所以端到端的下限就是后处理的基本性能。

2. 总体来说，MeanFlow和Flow Matching的关系是：MeanFlow 通过学习 平均速度场，并且通过这个速度场来生成样本，相比于 Flow Matching 的 瞬时速度场，它在 单步生成 和 训练稳定性 上具有优势。

3. Flow Matching 专注于瞬时速度场，它可以通过多步过程生成样本，但在推理阶段需要更多的步骤。

4. MeanFlow 的生成路径通常会是弯曲的，并且与数据的几何结构相一致，在低维视角下看，meanflow的速度流不是简单的直线。这样，它能够更好地捕捉到 数据分布的复杂性。但是在高维视角下，meanflow走的就是直线。

为了加深理解，git上找来了两个meanflow仓库，其中一个是作者提供的demo，使用的数据是CIFAR-10，可以玩一玩。同时我也拉到了本地做了一些修改，有兴趣可以看下：

https://github.com/haidog-yaqub/MeanFlow#，https://github.com/Gsunshine/meanflow。

首先我们要澄清meanflow中的数学符号的特殊定义方式：

Mean flow的数学符号和flow matching几乎没有区别，除了对起点和终点的定义有所不同。在meanflow中t=1 是“噪声端”（如高斯），t=0 是“数据端”，一般来说在flow matching中我们通常会将t = 0定义为噪声，然后delta_向前多步去噪到达数据分布，t = 1. 在meanflow中反过来的操作原因是因为公式书写方便，因为一步去噪的表示是：

如果我们反过来，就是把t_0作为噪声，那z_1就是数据分布，我们是不能先验知道数据分布的，也就不知道改怎么采样了，所以就不可能一步去噪，只能再次回到多步采样的策略。 核心就是为了我们数学定义和推理的方便。下面给gpt的详细推导：

然后给出meanflow的基本特点总结：

最后给出meanflow的伪代码：

下面给出mean flow的推理过程，逐步给出meanflow的目标函数，以及建立reflow and mean flow之间的联系。数学公式预警，请不要看：

reflow给出的目标函数是优化速度流平均期望：

而在推理阶段使用欧拉离散积分：

由于reflow学习的瞬时流，在推理阶段直接使用一步去噪肯定会让效果大打折扣，而diffusion model被诟病的一个很大的问题就是生成效率问题，所以我们又希望能够让模型一步去噪，或者few step去噪，所以提出了meanflow。对形如如下式的ODE：

进行两端积分：

 如果能够建模上面的积分结果表示的平均速度：

这样我们就可以直接一步去噪：

推导的基本思路就是通过构建两个恒等变化，建立起瞬时速度和平均速度的关系。然后利用这两个恒等变化带入reflow的目标函数中的到meanflow的训练目标。生成扩散模型漫谈（三十）：从瞬时速度到平均速度 - 科学空间|Scientific Spaces这里面的推导写的非常清楚，这里就不再重新写一遍了：

整个过程，我们注意到最后的推导结果就是：

这个和上面的伪代码是匹配的，只是stop grad在伪代码中套在了最外层，但sg(x_1 - x_0)套不套没有影响。

MeanFlow Toy eg

用https://github.com/haidog-yaqub/MeanFlow里面的简单例子试一下meanflow：

Flow matching vs Diffusion

Flow matching和diffusion是一类方法的总称。不同的设计调整会有不同的名字。我们整体对比一下flow matching and diffusion（我们常说的diffusion一般指denoising diffusion model，由于原论文是denoising diffusion probability model，所以diffusion也叫DDPM，另外一般我们也可以称diffusion为为score matching方法，与flow matching都是matching方法，一个matching log prob score，一个matching 速度场flow）。

下面回答一个问题，为什么diffusion必须要初始分布为Gaussian。总结来说就是：

• 在 Diffusion 框架中，训练需要对 pt(xt∣x1) 进行采样。

• 这个分布是通过 SDE (随机微分方程) 推导得到的，假设初始噪声 x_0服从高斯分布。

• 只有高斯分布在 SDE 下才能保证：

• • 闭式解存在（高斯的线性变换还是高斯）。

  • 梯度（score function ∇xlog⁡p）容易计算。

如果 p(x0)不是高斯，闭式解就不存在，（高斯在仿射变换与加法下封闭，所以高斯才有闭式解）。无法高效训练。训练阶段的闭式监督值来自“线性漂移 + 高斯增量”；生成阶段的可行性与稳定性则受益于把最噪端边际 p(x0) 设为高斯。

下面证明：

总结来说，我们需要依赖gaussian分布的可采样起点，他不可以与数据分布相关。其次，我们还需要边界score function可知，因为我们需要它的解析解。最后为了在整个时间轴上进行推导，其中涉及到积分，所以我们还要依赖gaussian的线性和卷积操作封闭的特性。

概率流ODE下的统一框架

基于SDE的score matching方法就是基于朗之万采样的，而基于ODE的flow matching则是学习整体速度场，但是s_theta和u_theta其实是可以互相转化的，为什么一个要依靠噪声跳出局部最优，一个却被描述为在学习全局的速度场。两者是否有关联呢，答案是肯定的。score matching和flow matching的表达可以同意下概率流ODE的框架下。我们首先给出结论：

• Score Matching (SDE/ODE) 和 Flow Matching 本质上是同一个家族：

• • 前者通过学 s_\theta，再转为速度；

  • 后者直接学 u_\theta。

• 噪声的角色：

• • 在 经典 EBM Langevin：必要，用来遍历分布；

  • 在 score-based diffusion：只是在选择 SDE 形式时自然出现的，理论上可替代为 ODE。

  • 在 flow matching：直接学速度场，不需要噪声。

所以，“一个要靠噪声跳出局部最优，一个学全局速度场”的说法，其实混合了 EBM Langevin 和 score-based diffusion。 更准确的说法是：

• EBM + Langevin：确实需要噪声避免局部模态；

• Diffusion (score-based)：可以用 SDE（有噪声）或 ODE（无噪声）；

• Flow Matching：直接 ODE，无噪声。

下面是证明预警，请全部跳过。

我们的证明思路是通过FP equation刻画 SDE 的分布演化，用CE（continuity equation）刻画 SDE 的分布演化，然后证明在给定特殊形式下的f(x)两者等价。而这个特殊形式就是：

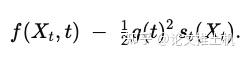
首先介绍什么是概率流ODE：

然后开始证明：

在这里step3中的展开CE方程的具体做法如下：

Classifier free guidance

无分类器引导技术为diffusion可控生成提供技术支持。使用diffusion的一大需求就是可控生成。例如，我们可以想象一个图像生成模型，它接收一个文本提示 y ，然后根据 y 生成图像 x 。为了避免使用"conditional"一词来指代基于 z∼p_data 的条件（条件概率路径/向量场）时与符号和术语产生冲突，我们将使用"guided"这一术语来特指基于 y 的条件。带上guidance之后，推理过程就变成了：

这是一般形式，当随机噪声=0的时候，这个表达就是guided flow model。

guidance下的u_target表达方式的推导主要利用到了贝叶斯公式。由于这个guidance很重要，这里还是给出全部推导过程，推导中为了简单明了，所以采用了gaussian path下的u_target表示，也就是(65)中的简明表示。由于公式太多就直接截图了：

w=4下的训练结果可以看到柯基狗guidance受到了很好的跟踪：

可以看到，按道理来说为了学习guided情况下的u_target，我们应该要学习一个guided和一个unguided 版本的u_target。事实上，早期的diffusion model就是这么做的。但是现代diffusion方法中，我们使用了CFG技术，不再需要显式地学习guided u_target了。

在CFG中，我们引入w来调整guided u_target和unguided u_target的均衡。并且通过统一表达式，也就是使用condition on空集的策略，将guided和unguided统一表达，代码实现中也是通过引入一个special label用于表示空集所代表的不存在的guidnace来表示unguided。

现在给出CFG training的伪代码：

在代码实现中，我们通常的做法是：

这里面的：

这个公式的推导方式是：

CFG和condition有什么关系

“编码→生成时调制”（conditioning）指的是把条件 喂进扩散模型（比如U-Net）的方法本身：比如文本编码器→Cross-Attention、把条件做成额外通道、或者用FiLM/AdaNorm之类的特征调制。这是模型结构/训练层面的事，决定了模型学到的 是什么样。也就是说condition的是在模型层面通过编码来表示的。

CFG（Classifier-Free Guidance）是推理/蒸馏阶段的一种强度控制：把“有条件预测”和“无条件预测”线性外推 。它不改变网络怎么接收条件，只是在采样时（或训练蒸馏时）放大条件的影响。

两者一般是一起用的，一个是在编码condition，一个是在设计学习目标，从而达到模型follow condition的目标。

Diffusion on Planning

这个后面再写，我们会整理一些diffusion在planning的应用的论文，然后讨论其合理性。

自动驾驶之心

论文辅导来啦

自驾交流群来啦！

自动驾驶之心创建了近百个技术交流群，涉及大模型、VLA、端到端、数据闭环、自动标注、BEV、Occupancy、多模态融合感知、传感器标定、3DGS、世界模型、在线地图、轨迹预测、规划控制等方向！欢迎添加小助理微信邀请进群。

知识星球交流社区

近4000人的交流社区，近300+自动驾驶公司与科研结构加入！涉及30+自动驾驶技术栈学习路线，从0到一带你入门自动驾驶感知（大模型、端到端自动驾驶、世界模型、仿真闭环、3D检测、车道线、BEV感知、Occupancy、多传感器融合、多传感器标定、目标跟踪）、自动驾驶定位建图（SLAM、高精地图、局部在线地图）、自动驾驶规划控制/轨迹预测等领域技术方案、大模型，更有行业动态和岗位发布！欢迎加入。

独家专业课程

端到端自动驾驶、大模型、VLA、仿真测试、自动驾驶C++、BEV感知、BEV模型部署、BEV目标跟踪、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、车道线检测、轨迹预测、在线高精地图、世界模型、点云3D目标检测、目标跟踪、Occupancy、CUDA与TensorRT模型部署、大模型与自动驾驶、NeRF、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频

学习官网：www.zdjszx.com