前言:前端路径规划搜索出来的路径虽然是无碰撞的,但是没有考虑机器人的动力学(v,a,jerk等),生成的路径不光滑,且不含时间参数。机器人的状态不能突变,只能走走停停,浪费时间和效率。
后端轨迹优化,使用minimum snap 对前端给的waypoiints分段多项式拟合,得到光滑的,考虑动力学约束的轨迹。
闭式求解(解析求解)与数值求解相对
数值求解:通过迭代计算,一步步逼近问题的解。但是得不到一个解的精确的公式,但能得到一个高精度的数值解。例如,用梯度下降法求解最优问题。(二分法,牛顿法去迭代计算,最终得到一个非常接近真实解的数值)
闭式求解(解析求解):通过一系列公式推导,最终将解值解表示成某个矩阵的逆乘以某个向量(比如这里mini snap就是:Ad=P,d=A的逆乘P),可以得到一个精确的数学公式。避免数值优化的迭代过程,计算速度快。
1.minimun snap 的代价函数中的Q矩阵
K段轨迹,K+1个点,K-1个中间点。K段轨迹中任何一个轨迹都可以用如下向量相乘形式写出:
可以看见,n (n=2*s-1)次多项式,有n+1个未知系数。
这里是minimum sanp ,s=4,n=6。一个起点,一个终点,2个中间点,3段轨迹。对多项式求3阶导的snap为:
这是一个无约束的二次规划问题(QP)。对于其中一段轨迹(每段使用相对时间分配,梯形速度分配):
目标函数:
明显可以看出Qi:(n+1)x(n+1),为对称矩阵。Qi的结构特点如下所示:
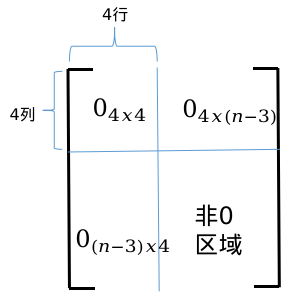
对于所有K段轨迹,总的代价函数为所有段轨迹的Qi之和:,其中Q为对称矩阵,k(n+1)×k(n+1)大小。
代码中,getQ()函数重点部分是如何写出Qi矩阵的解析形式:Qi矩阵中每个元素的解析形式为:,其中i:行数,j:列数。Q如下所示:
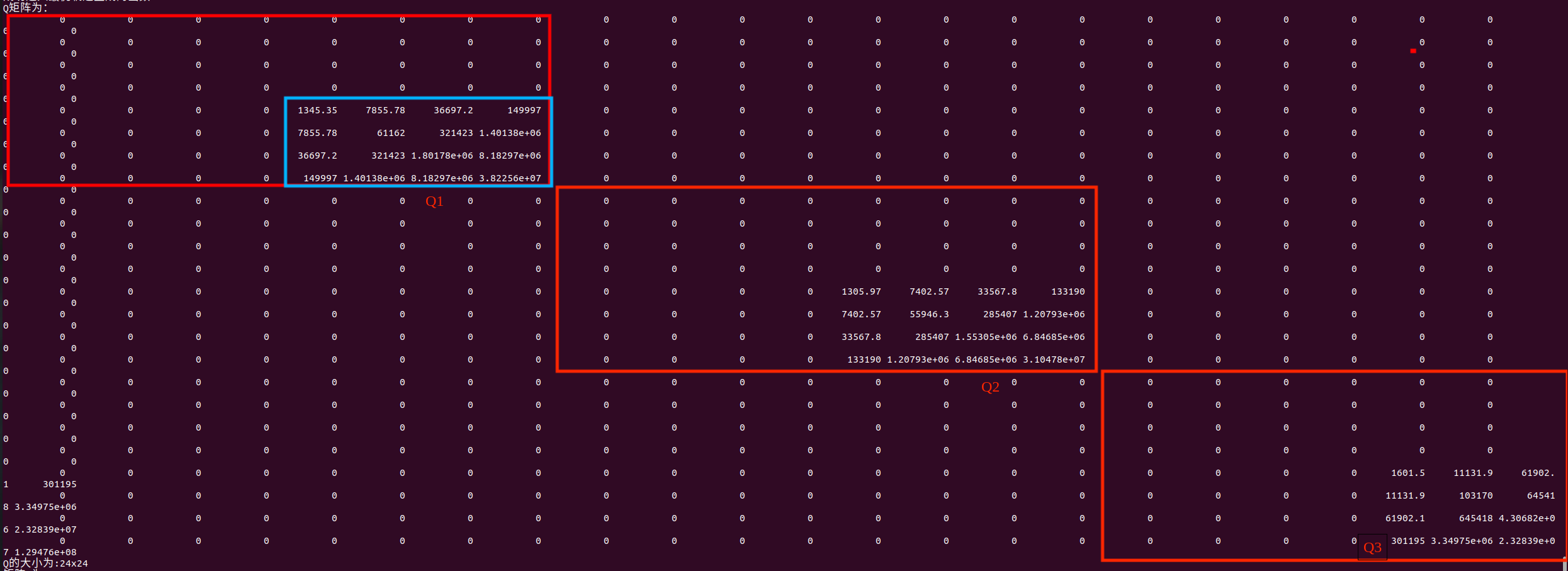
判断Q矩阵是否正确:1、Qi矩阵个数是否等于k。2、矩阵结构是否如上所是,满足对称矩阵性质。3、每个Qi矩阵里的非0部分,一般为正数。
目前成功构建了目标函数,只是初步满足了光滑。但是我们需要轨迹经过前端给的路径点和起点和终点,且在中间点处是高阶连续的。因此,需要加入约束。
2.将约束条件通过数学方法转换到代价函数中
2.1.微分约束构建AP=d
对于一段轨迹pi的两端进行分析,p,v,a,jerk的微分约束。:
对应代码实现部分:是对snap情况单独进行了讨论,然后用系数和相对时间,对Ai矩阵进行元素赋值。由于使用相对时间,所以前4行关于时间t的元素都为0,A如下所示:
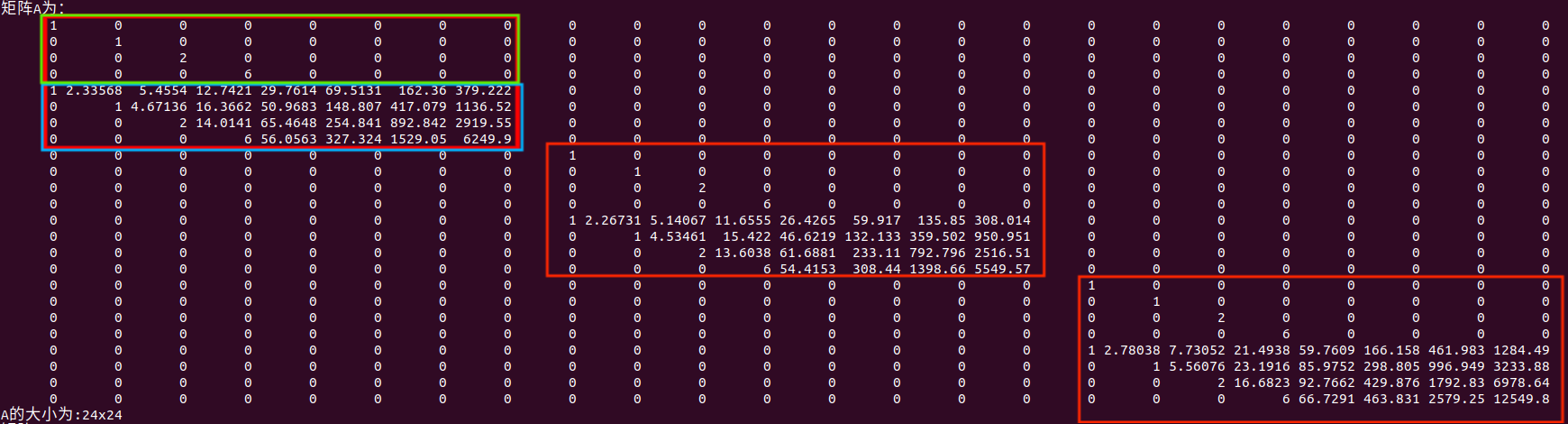
所有轨迹多项式P的解析解形式为:,
,dp为未知状态。P为所有轨迹段的所有系数,d为所有k段轨迹的两侧端点的微分约束(p,v,a,jerk)
2.2.加入连续性约束(同时还消除了重复变量)
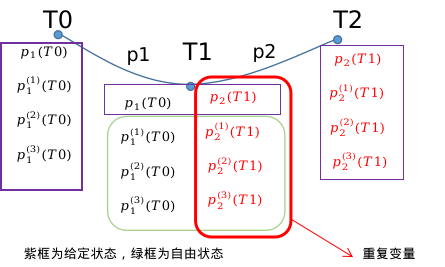
构造MC矩阵的代码逻辑:1、起点的4个给定约束。2、中间(k-1)个点的给定位置与位置连续性。3、末尾点给定4个约束。4、中间(k-1)个点的v,a,jerk高阶约束与连续性约束。
代码逻辑如上图,通过一个映射和装置矩阵MC,将。注:这里的自由状态在等式里面没有设置为0,而是作为未知变量,通过
求解最优的dp。这一部分的矩阵映射,只是对d(给定所有点的导数约束)进行处理,消除了重复的导数变量,但是利用连续性约束,使得导数约束不变,并加入了连续性约束。
MC矩阵如下所示,可以通过s的大小,轻易推断出这个MC是否正确。
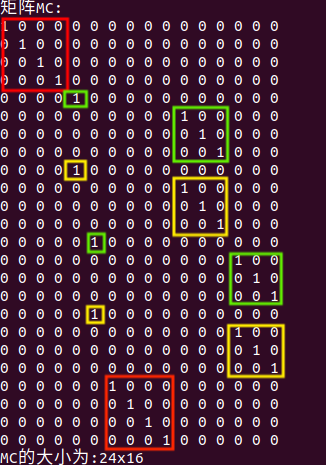
2.3、解析求解P
step 1:求解dp
前面的Q,A,d,P都是讨论的单轴,从这里开始,分别单独计算3个轴的dp,和P
将P带入目标函数中得:

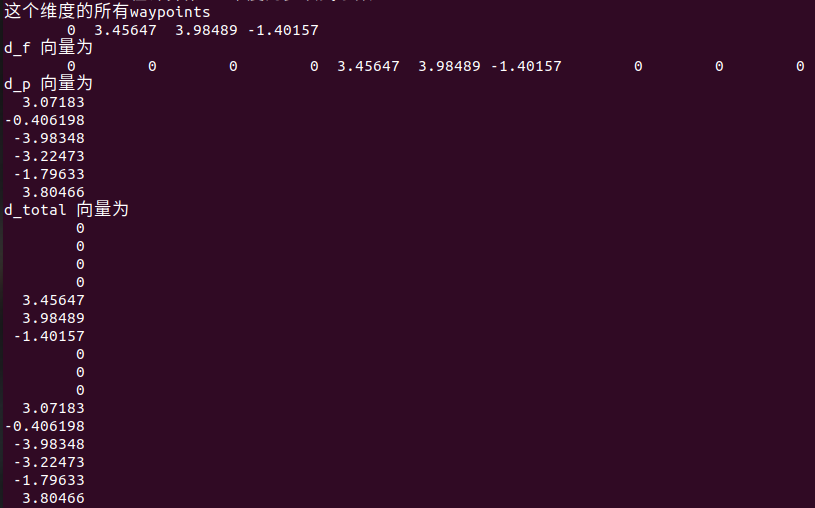
注:最后目标函数J是dp的函数,由于我们的目标是最小化J,所有使得J最小的dp就是我们要的最优dp。所以对J求偏导为0,得到的dp就是最优dp。此时的J也是最小的J。但是我们要求的是轨迹多项式的系数P,所以,需要继续把求出来的dp带入中,其中A为关于每段轨迹端点时间的矩阵(时间分配后,A为已知),MC为常量稀疏矩阵(已知),df为给定状态,dp上方求出。最后可以带入,求出P。
step 2:求解P
//-----------------通过p的解析解形式,求解一个维度的所有多项式系数--------------------//
Eigen::VectorXd poly_coef_1d = A.inverse() * MC *d_total;
cout<<"Dimensoin"<<dim<<"cofficients:"<<endl<<poly_coef_1d.transpose()<<endl;
这里有3段轨迹,且我们最后计算了三轴所以P大小为(k)×(3(n+1))
PolyCoeff = [段0_x系数 段0_y系数 段0_z系数]
[段1_x系数 段1_y系数 段1_z系数]
[段2_x系数 段2_y系数 段2_z系数]
[ ... ... ... ]

判断最后求的得矩阵P是否正确:看前几段轨迹系数是否出现很大的值,如xxe+15这类的,那P求解错误。
轨迹生成调试方法:
1.可视化轨迹,发现话题没有输出,rviz中没有估计,大概率P求解错误
2.在可视化之前,打印轨迹的前几个点,看点是否和实际点符合,如:
// 打印前几个点的坐标
if(_traj_vis.points.size() > 0) {
cout << "First few trajectory points:" << endl;
for(int i = 0; i < min(5, (int)_traj_vis.points.size()); i++) {
cout << " Point " << i << ": ("
<< _traj_vis.points[i].x << ", "
<< _traj_vis.points[i].y << ", "
<< _traj_vis.points[i].z << ")" << endl;
}
}
cout<<"可视化点的数量:" << _traj_vis.points.size() << endl;
if(_traj_vis.points.empty()) {
cout << "WARNING: No trajectory points to publish!" << endl;
return;
}
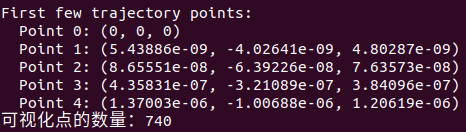
上面图片的点就是符合实际情况的(根据自己在rviz中选的点来判断)。如果出现了特别大的点,那就是系数求解有问题,回去看是df,A,MC,Q谁有问题。
成功轨迹优化图片:

总结:闭式求解过程
1.建立目标函数
2.写出Q矩阵的形式(对称矩阵)
3.微分约束建立起,连续性约束得到
4.将P的解析形式带入目标函数中,得到J关于dp的函数,最小化J求dp。最后将dp带入值解求解P。




















 780
780

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








