逻辑回归的损失函数

逻辑回归是在线性函数的基础上，经过激活函数后产生的0~1之间的概率值。
设x为特征向量，y为真实的标签。$\hat{y}$是预测值。得出：

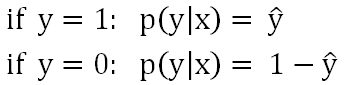
两个合并起来写为：

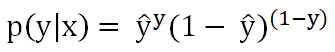
看等式左边的$P(y|x)$，我们可以解读为给定特征向量x，模型能正确预测出y的能力。这个值总是大于0小于1的。越接近1说明能力越强。
其实这个式子被成为似然函数，意思是预测结果靠近或者接近真是值的程度。我们想要模型更好，这个似然函数的值就要越大。
极端一点，这个模型就是最最好的那个。带入式子中就是，x是正样本，似然函数就等于1，这时候$\hat{y}$=1.x是负样本，似然函数也等于1，KaTeX parse error: Expected group after '\hat' at end of input: \hat=0.所以我们的目标就是要最大化似然函数。
以往的线性回归模型，使用的都是最小二乘法作为损失函数，大意就是用预测值与真实值的差作为评价模型好坏的标准。毕竟越好的模型预测的应该越准确嘛。
但这里却没用最小二乘作为损失函数，为什么呢？因为线性回归是回归问题，而逻辑回归虽然叫逻辑回归，实则确实分类问题。类别变量不同于连续变量，连续变量可以用差距衡量模型的好坏，分类问题却只是用数值代表类别，数值本身确实无意义的，比如用{0，1}表示的类别，用{1，2}也同样能够表示。经过学习我们知道，类别问题更应该用概率分布的角度衡量预测出的类别与真实类别的差距。
接着之前的讲，我们要好的模型，就要最大化似然函数。这里用一个小技巧，把似然函数两边取对数，得到对数似然函数，因为对数函数是单调递增的，所以最大化似然函数等价于最大化似然函数。

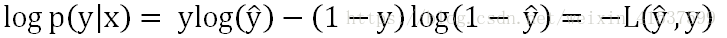
在讲这个对数似然函数之前，我们要提一下“损失函数”，损失函数：真实值-预测值=损失掉的值。机器学习中，总是希望损失函数的值越小越好。所以，我们希望最大化对数似然函数，就可以让损失函数等于负的对数似然函数，那么对数似然函数越大，损失函数不就越小了么。
上式中的大写L就是代表损失函数。
最大化似然函数也就是最小化损失函数。
对于m个样本的整个训练集，服从独立同分布的样本的联合概率（样本与样本没有关联）就是每个样本的概率的乘积：

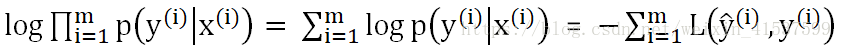
同样的，最大化似然函数也就是最小化代价函数，因此可以去掉负号，并除以一个常数m对代价函数进行适当的缩放，得到：

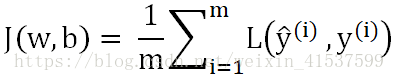
参考：https://blog.youkuaiyun.com/weixin_41537599/article/details/80585201