【代码超详解】LightOJ 1234 Harmonic Number（技巧，260 ms）

原创于 2020-02-29 15:42:01 发布 · 306 阅读

1 ·

CC 4.0 BY-SA版权

ACM-ICPC 专栏收录该内容

238 篇文章

订阅专栏

本文介绍了一种在时间和内存限制下计算第N个调和数的算法。通过间隔存储累加结果，避免了全量计算带来的资源消耗。采用2的正整数次方间隔，利用位运算优化计算效率。

一、题目描述

Time limit
3000 ms
Memory limit
32768 kB
OS
Linux
Source
Problem Setter: Jane Alam Jan

In mathematics, the nth harmonic number is the sum of the reciprocals of the first n natural numbers:
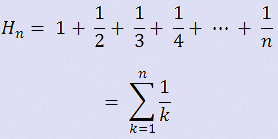
在这里插入图片描述
In this problem, you are given n, you have to find Hn.

Input

Input starts with an integer T (≤ 10000), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 108).

Output

For each case, print the case number and the nth harmonic number. Errors less than 10-8 will be ignored.

Sample Input

Sample Output

Case 1: 1
Case 2: 1.5
Case 3: 1.8333333333
Case 4: 2.0833333333
Case 5: 2.2833333333
Case 6: 2.450
Case 7: 2.5928571429
Case 8: 2.7178571429
Case 9: 2.8289682540
Case 10: 18.8925358988
Case 11: 18.9978964039
Case 12: 18.9978964139

二、算法分析说明与代码编写指导

三、AC 代码（260 ms）

n 最大达到 10^8，打表存下结果会超时。而且本题的内存限制是 32 MB，也没有办法存储这么长的结果（一个 double 变量占 8 字节）。
我们可以间隔一定距离来存储累加的结果。例如本代码只存储 H32，H64，H96，……。
在计算 Hn 的时候，将最后一截未存储下来的部分累加即可。
间隔选用 2 的正整数次方是因为 x % 2^n 会被编译器优化为 x & (2^n - 1)，将花费周期较长的取模运算转化成花费周期较短的位运算。

#include<cstdio>
#include<cmath>
#pragma warning(disable:4996)
const unsigned smax = 100000001;
double h[smax / 32 + 1], s, t; unsigned T, n, r;
int main() {
	for (unsigned i = 1; i < smax; ++i) {
		s += 1.0 / i;
		if (i % 32 == 0)h[i / 32] = s;
	}
	scanf("%u", &T);
	for (unsigned i = 1; i <= T; ++i) {
		scanf("%u", &n); r = n % 32; t = 0;
		for (unsigned i = 1; i <= r; ++i)t += 1.0 / (n - r + i);
		printf("Case %u: %.10lf\n", i, h[n / 32] + t);
	}
	return 0;
}