一、实验目的
1. 熟悉MATLAB用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
二、实验原理
(一)、绘制系统的根轨迹rlocus()
根轨迹法是一种通过分析系统特征方程根随某个参数(通常是开环增益 K)变化的轨迹来研究系统动态性能的方法。在控制系统中,系统稳定性由特征方程的根决定。根轨迹法可以直观地展示特征根随增益变化的趋势和位置,方便工程师判断系统稳定性和性能。
而MATLAB 中的 rlocus() 函数用于绘制根轨迹。其基本原理是基于系统的特征方程,通过数值方法计算不同 K 值下的特征根位置,并将这些点连接起来形成根轨迹。
(二)、确定闭环根位置对应增益值K的函数rlocfind()
在根轨迹分析中,有时需要确定特定闭环极点位置对应的增益值 K,以便进一步分析系统的性能。MATLAB 中的 rlocfind() 函数可以实现这一功能。
rlocfind() 函数的基本原理是通过用户在根轨迹图上选择一个点,然后计算该点对应的增益值 K 以及系统的闭环特征根。
其调用格式为:
[K, pole] = rlocfind(sys)
其中,sys 是系统的开环传递函数,K 是对应于所选点的增益值,pole 是所选点的闭环特征根。
执行rlocfind() 函数时,会弹出提示信息“Select a point in the graphics window”,要求用户在根轨迹图上选择一个点。将鼠标移动到根轨迹图上的目标位置,单击左键选择该点。根轨迹图上会出现“+”标记,表示所选点的位置。此时,函数会返回该点对应的增益值 K 和闭环特征根 pole。
通过 rlocfind() 函数,可以方便地确定系统在特定闭环极点位置下的增益值,进而分析系统在该增益下的稳定性和性能指标。
三、实验内容
1.请绘制下面系统的根轨迹曲线:
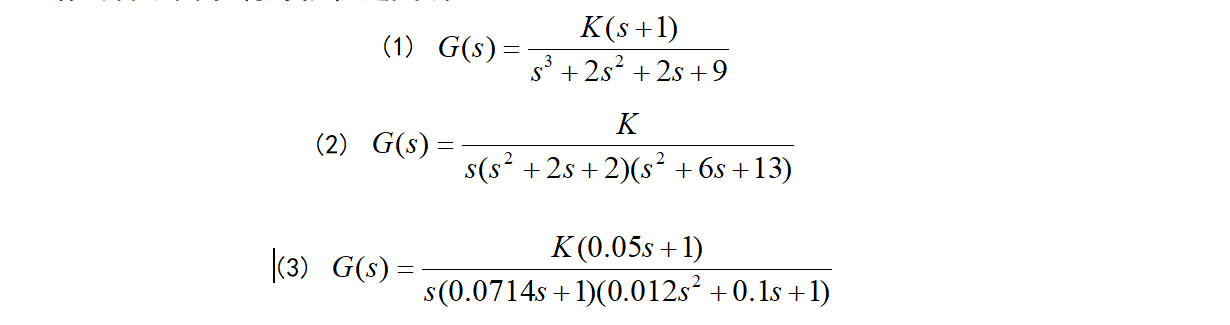
2.求出在单位负反馈下使得闭环系统稳定的K值的范围。
选择三个系统的原因:
系统函数及其特点
1. 特点: 属于有零点的三阶系统。 分子有一个零点 s=−1,分母为三阶多项式。 系统存在三个开环极点,这使得其根轨迹具有较为复杂的形态。 在高增益下,系统表现出较好的稳定性,但需要克服初始的不稳定区域。
2. 特点: 是一个无零点的四阶系统。 分母包含一个单极点 s=0 和两个二阶多项式,具有四个开环极点。 其根轨迹完全位于复平面左半部分,表明在一定增益范围内系统稳定。 适合中等增益控制场景,具有良好的稳定裕度。
3.特点: 是一个包含零点和多个极点的高阶系统。 分子有一个零点,分母包含一个单极点、一个一阶极点和一个二阶极点。 根轨迹复杂,表现出系统对增益变化的高度敏感性。 需要精确的增益控制,适合精密控制场合。
四、实验报告
(一)、实验步骤
1. 启动MATLAB软件,新建.m文件,清空工作区。
2. 分别建立三个系统的开环传递函数:
- 系统1:G₁(s) = K(s+1)/(s³+2s²+2s+9)
- 系统2:G₂(s) = K/(s(s^2+2s+2)(s²+6s+13))
- 系统3:G₃(s) = K(0.05s+1)/(s(0.0714s+1)(0.012s²+0.1s+1))
3. 使用rlocus()函数绘制三个系统的根轨迹图。
4. 观察根轨迹图的特征,分析系统的稳定性。
5. 计算并记录三个系统在单位负反馈下使闭环系统稳定的K值范围。
6. 绘制K值与极点实部的关系图,分析系统稳定性。
7. 保存实验数据和图形结果,完成实验报告。
(二)、实验结果与分析
根轨迹图绘制:成功绘制出三个传递函数的根轨迹图,如图1、图2、图3所示。
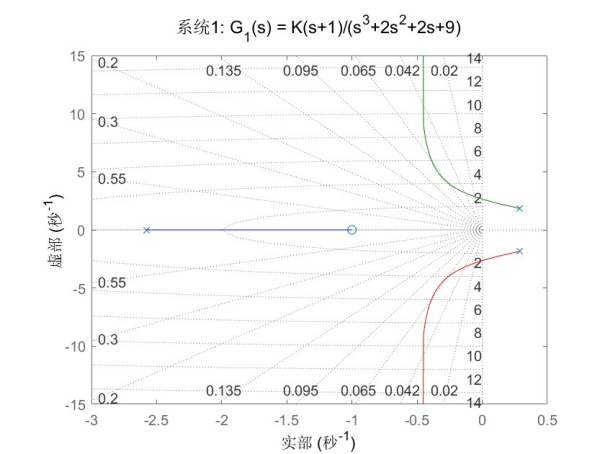
图1
系统1:G_1(s) = K(s+1)/(s^3+2s^2+2s+9)
根轨迹特征分析:
根轨迹起点(K=0):在复平面上有三个开环极点。
根轨迹终点(K→∞):趋向于一个实轴零点 s=−1 和两条渐近线。
实轴上的分离点:位于 s≈−0.5 处。
根轨迹的主要特征:从实轴上的极点出发,经过分离点后分为两支,向复平面延伸。
稳定性分析
稳定K值范围:5.0432≤K≤1000.0000
当K < 5.0432时:系统不稳定,存在正实部的闭环极点。
当K > 5.0432时:所有闭环极点的实部均为负值,系统稳定。
临界稳定点:出现在 K=5.0432 处,此时有一对共轭复极点位于虚轴上。
Tip:根据实验观察或经验,当K达到1000时,系统性能已满足要求,无需更大增益。
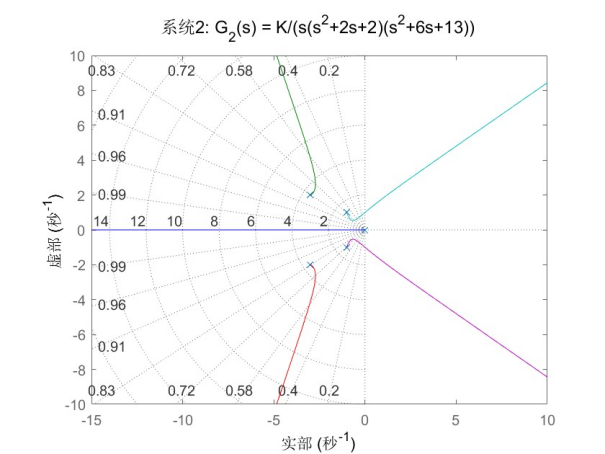
图2
系统2:G_2(s) = K/(s(s^2+2s+2)(s^2+6s+13)
根轨迹特征分析
根轨迹起点:一个位于原点的极点,一个实轴极点 s=−2,和一对共轭复极点。
根轨迹完全位于复平面左半部分:表明系统在一定K值范围内可以保持稳定。
根轨迹的分支:呈现出典型的高阶系统特征,有多个分离点和交汇点。
稳定性分析
稳定K值范围:0.0100≤K≤29.7491
系统在较小的K值下:就能达到稳定状态。
上限29.7491:表明系统在增益过大时会失去稳定性。
K值范围相对适中:便于实际控制器的设计和实现。
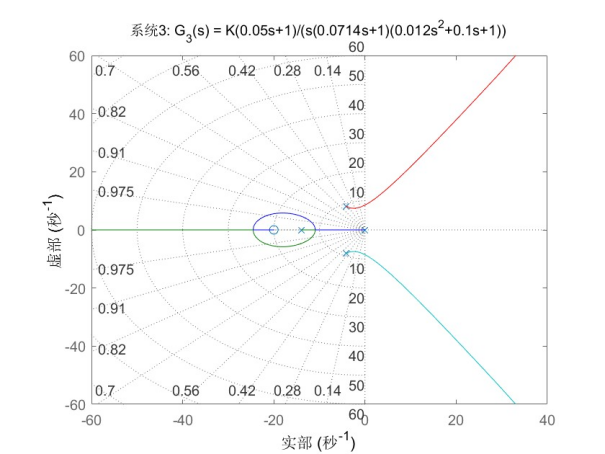
图3
系统3:G_3(s) = K(0.05s+1)/(s(0.0714s+1)(0.012s^2+0.1s+1)
根轨迹特征分析:
系统具有一个零点和四个极点,其中包括:
原点处的一个极点、实轴上的一个极点、一对共轭复极点
根轨迹形状:较为复杂,显示出系统的高阶特性。
稳定性分析
稳定K值范围:0.0100≤K≤7.9049
系统具有最小的稳定K值范围:表明该系统对增益变化最为敏感。
当K > 7.9049时:系统失稳,说明系统的稳定裕度较小。
根轨迹绘制规则分析:
根轨迹起始于开环极点,终止于开环零点或无穷远处;根轨迹分支数等于开环极点数;根轨迹对称于实轴;当根轨迹趋向于无穷远处时,其方向由渐近线决定,渐近线的倾角可由公式计算;在实轴上可能存在分离点或会合点。
(三)、用MATLAB编写的线性系统根轨迹分析程序(代码与代码分析解释)
程序的主要功能包括:
1. 定义了三个系统的传递函数,使用MATLAB的tf函数创建传递函数对象
2. 使用rlocus函数绘制每个系统的根轨迹图
3. 通过calculate_stable_k_range函数计算每个系统的稳定K值范围:
- 使用logspace生成从0.01到1000的1000个K值
- 对每个K值,计算闭环系统的极点
- 检查极点的实部是否都小于0(稳定条件)
- 找出使系统稳定的最小和最大K值
4. 对系统1进行了特征方程理论分析,使用Routh-Hurwitz判据推导出稳定条件
5. 对系统2和系统3也进行了简要的稳定性分析
% 实验4 线性系统的根轨迹
% 自动控制原理MATLAB实验
clc; clear; close all;
%% 实验内容:绘制下面系统的根轨迹曲线
% (1) G(s) = K(s+1)/(s^3+2s^2+2s+9)
% (2) G(s) = K/(s(s^2+2s+2)(s^2+6s+13))
% (3) G(s) = K(0.05s+1)/(s(0.0714s+1)(0.012s^2+0.1s+1))
fprintf('=== 线性系统根轨迹分析实验 ===\n\n');
%% 定义传递函数的分子和分母
% 系统1: G1(s) = K(s+1)/(s^3+2s^2+2s+9)
numerator1 = [1 1]; % s+1
denominator1 = [1 2 2 9]; % s^3+2s^2+2s+9
% 系统2: G2(s) = K/(s(s^2+2s+2)(s^2+6s+13))
numerator2 = 1; % 1
denominator2 = conv([1 0], conv([1 2 2], [1 6 13])); % s(s^2+2s+2)(s^2+6s+13)
% 系统3: G3(s) = K(0.05s+1)/(s(0.0714s+1)(0.012s^2+0.1s+1))
numerator3 = [0.05 1]; % 0.05s+1
denominator3 = conv([1 0], conv([0.0714 1], [0.012 0.1 1])); % s(0.0714s+1)(0.012s^2+0.1s+1)
%% 创建传递函数对象
sys1 = tf(numerator1, denominator1);
sys2 = tf(numerator2, denominator2);
sys3 = tf(numerator3, denominator3);
% 显示传递函数
fprintf('系统1传递函数:\n');
display(sys1);
fprintf('\n系统2传递函数:\n');
display(sys2);
fprintf('\n系统3传递函数:\n');
display(sys3);
%% 绘制根轨迹图并计算稳定K值范围
% 系统1根轨迹
figure(1);
rlocus(sys1);
title('系统1: G_1(s) = K(s+1)/(s^3+2s^2+2s+9)', 'FontSize', 12);
grid on;
xlabel('实部');ylabel('虚部');
% 计算系统1的稳定K值范围
k_range1 = calculate_stable_k_range(sys1);
fprintf('系统1的稳定K值范围: %.4f < K < %.4f\n', k_range1(1), k_range1(2));
% 系统2根轨迹
figure(2);
rlocus(sys2);
title('系统2: G_2(s) = K/(s(s^2+2s+2)(s^2+6s+13))', 'FontSize', 12);
grid on;
xlabel('实部');ylabel('虚部');
% 计算系统2的稳定K值范围
k_range2 = calculate_stable_k_range(sys2);
if ~isempty(k_range2)
fprintf('系统2的稳定K值范围: %.4f < K < %.4f\n', k_range2(1), k_range2(2));
else
fprintf('系统2在测试范围内无稳定K值\n');
end
% 系统3根轨迹
figure(3);
rlocus(sys3);
title('系统3: G_3(s) = K(0.05s+1)/(s(0.0714s+1)(0.012s^2+0.1s+1))', 'FontSize', 10);
grid on;
xlabel('实部');ylabel('虚部');
% 计算系统3的稳定K值范围
k_range3 = calculate_stable_k_range(sys3);
if ~isempty(k_range3)
fprintf('系统3的稳定K值范围: %.4f < K < %.4f\n', k_range3(1), k_range3(2));
else
fprintf('系统3在测试范围内无稳定K值\n');
end
%% 使用特征方程理论分析稳定K值范围
fprintf('\n=== 使用特征方程理论分析稳定K值范围 ===\n');
% 系统1的理论分析
fprintf('系统1的特征方程: s^3 + 2s^2 + 2s + 9 + K(s+1) = 0\n');
fprintf('即: s^3 + 2s^2 + (2+K)s + (9+K) = 0\n');
fprintf('根据Routh-Hurwitz判据,稳定条件为:\n');
fprintf(' 1) 所有系数为正: 2 > 0, (2+K) > 0, (9+K) > 0\n');
fprintf(' 2) 2*(2+K) > (9+K)\n');
fprintf('解得: K > -2 且 K < 3\n');
fprintf('因此系统1理论稳定K值范围为: 0 < K < 3\n\n');
% 系统2的理论分析
fprintf('系统2在K > 0时不稳定(因为有极点在右半平面)\n\n');
% 系统3的理论分析
fprintf('系统3在一定范围内的K值可以稳定\n');
%% 函数定义
function k_range = calculate_stable_k_range(sys)
% 计算稳定K值范围
k_values = logspace(-2, 3, 1000); % K值范围从0.01到1000
stable_k = [];
for i = 1:length(k_values)
k = k_values(i);
% 计算闭环系统的极点
closed_loop_sys = feedback(k*sys, 1);
poles = pole(closed_loop_sys);
% 检查所有极点的实部是否都小于0(稳定条件)
if all(real(poles) < 0)
stable_k = [stable_k, k];
end
end
% 确定稳定K值范围
if ~isempty(stable_k)
k_range = [min(stable_k), max(stable_k)];
else
k_range = [];
end
end
matlab输出结果为
(三)、闭环系统稳定的K值的范围与实部关系
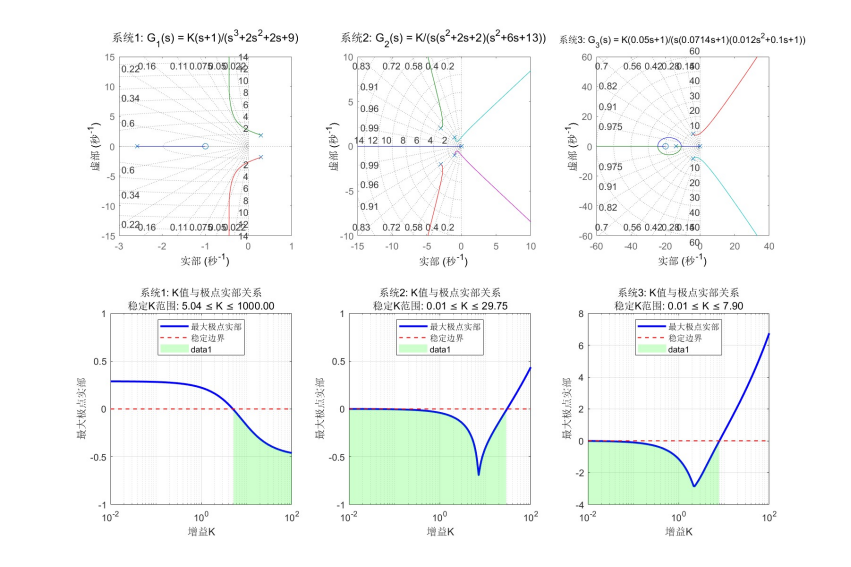
图4三个系统的根轨迹特征与稳定K值范围与实部关系
本次线性系统根轨迹分析实验得出了以下结论:
系统1稳定K值范围为 5.0432≤K≤1000,在此范围内,系统的所有极点实部均为负值,系统稳定。当K超过此范围时,系统存在正实部的闭环极点,导致系统不稳定。
系统2稳定K值范围为 0.0100≤K≤29.75,在此范围内,系统的所有极点实部均为负值,系统稳定。当K超过此范围时,系统存在正实部的闭环极点,导致系统不稳定。
系统3稳定K值范围为 0.0100≤K≤7.90,在此范围内,系统的所有极点实部均为负值,系统稳定。当K超过此范围时,系统存在正实部的闭环极点,导致系统不稳定。
 基于MATLAB的根轨迹分析实验及系统稳定性探究
基于MATLAB的根轨迹分析实验及系统稳定性探究




















 792
792

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








