【leetcode hot 100 】(数组、二分) 704 二分查找+y总模板+35 搜索插入的位置

1.原题

2.思路

二分法介绍

1. 假设目标值在闭区间[l,r]中
2. 每次将区间长度缩小一半
3. 当 l == r 时，找到目标值

应用：本质是查找满足某个性质的边界点

1. 找到大于等于数的第一个位置(满足某个条件的第一个数)
2. 找到小于等于数的最后一个位置(满足某个条件的最后一个数)
3. 查找最大值
4. 查找最小值

涉及到边界条件，很容易写错

---

难在边界问题

y总模板：

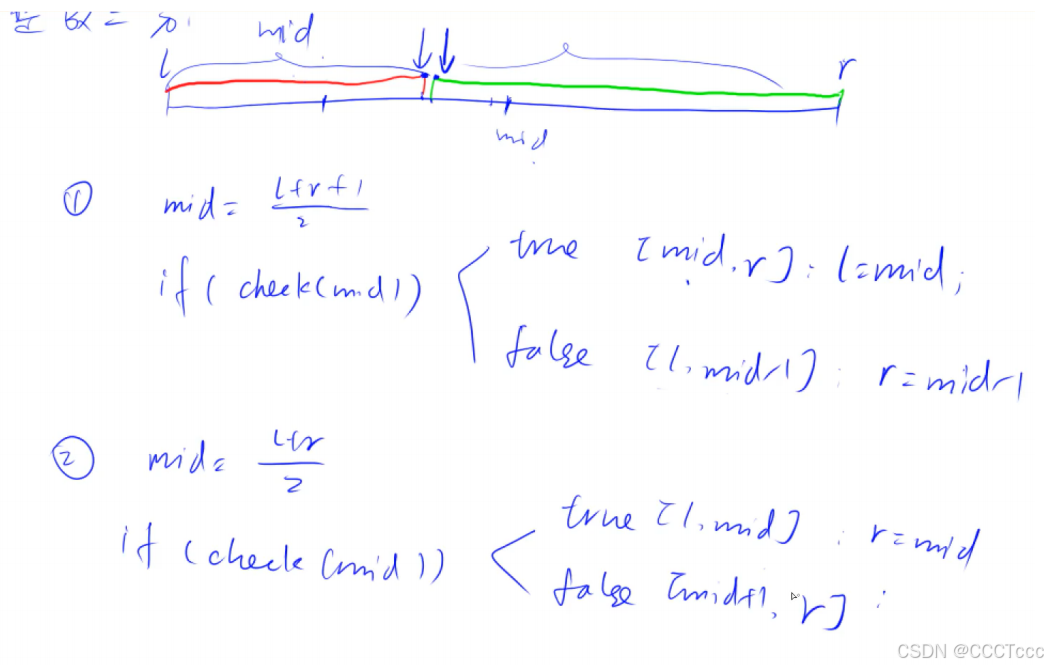
1. 将区间 [l , r] 划分为 [ l, mid ] 以及 [ mid + 1, r ]
2. 区间边界更新操作是 r = mid 或者 l = mid + 1;
3. 中点是 mid = l + r >> 1;

（l+r）/2 后 下取整

//适用于：查找有序数组中的左边界。列如：在升序数组中找到第一个不小于target的索引。也就是图中绿色部分的最左边那个点
int search1(int l, int r)
{
	while(l < r)
	{
		int mid = l + r >> 1;
		if(check(mid)) r = mid;
		else l = mid + 1;
	}
	return l;
}

1. 将区间 [l , r] 划分为 [ l, mid - 1 ] 以及 [ mid , r ]
2. 区间边界更新操作是 r = mid - 1 或者 l = mid ;
3. 中点是 mid = l + r + 1 >> 1;

（l+r）/2 后 上取整

//适用于：查找有序数组中的右边界。列如：在升序数组中找到最后一个不大于target的索引。也就是图中红色部分的最右边那个点
int search2(int l, int r)
{
	while(l < r)
	{
		int mid = l + r + 1 >> 1;
		if(check(mid)) l = mid;
		else l = mid - 1;
	}
	return l;
}

关于中点mid的问题：

对于mid + 1与否，是为了让区间平分
mid = left + right >> 1; 这里mid是上中位数
mid = left + right + 1 >> 1; 这里mid是下中位数
如果取left = mid, 即[mid, right], 则mid取下中位数才能平分区间
如果取right = mid, 即[left, mid], 则mid取上中位数才能平分区间

3.整体代码

//用模板1
class Solution {
public:
    int search1(vector<int>& nums, int target) {
        int l = 0,r = nums.size()-1;
        while(l < r)
        {
            int mid = l + r >> 1;
            //这个nums[mid] >= target 类似于 找到左边界
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        if(nums[l] == target) return l;
        return -1;
       
    }
};

//用模板2
class Solution {
public:
    int search2(vector<int>& nums, int target) {
        int l = 0,r = nums.size()-1;
        while(l < r)
        {
            int mid = l + r + 1>> 1;
            //这个nums[mid] <= target 类似于 找到右边界
            if(nums[mid] <= target) l = mid;
            else r = mid - 1;
        }
        if(nums[l] == target) return l;
        return -1;
       
    }
};

模板1的图示：

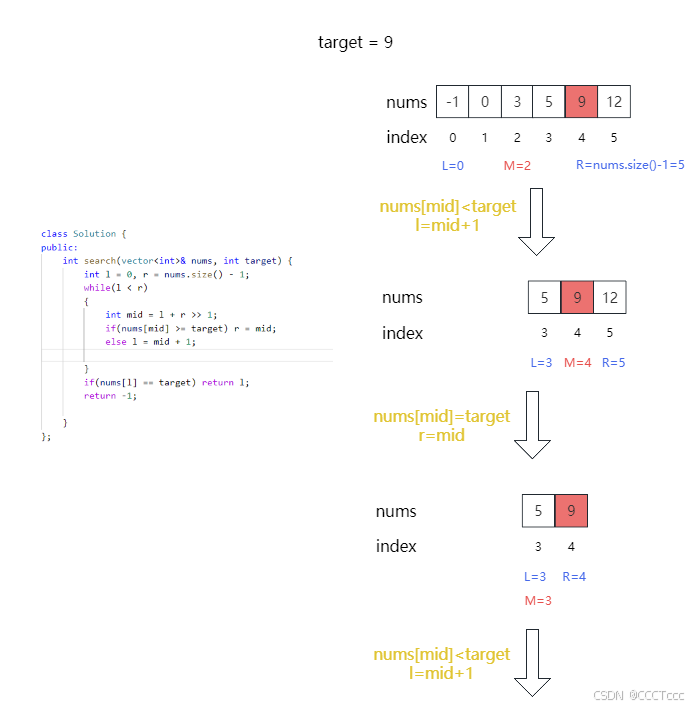
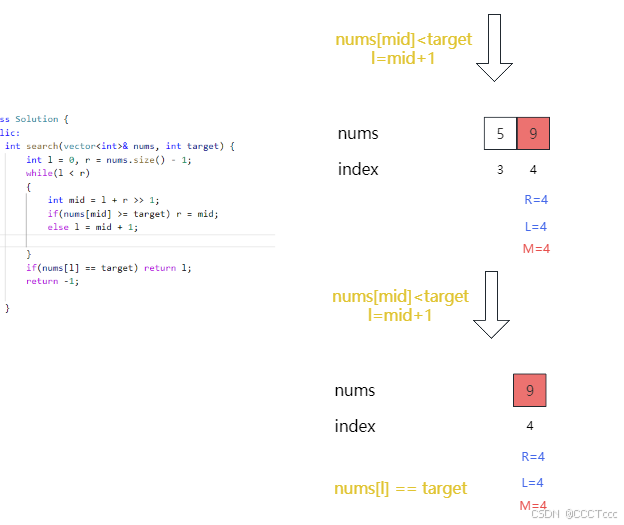
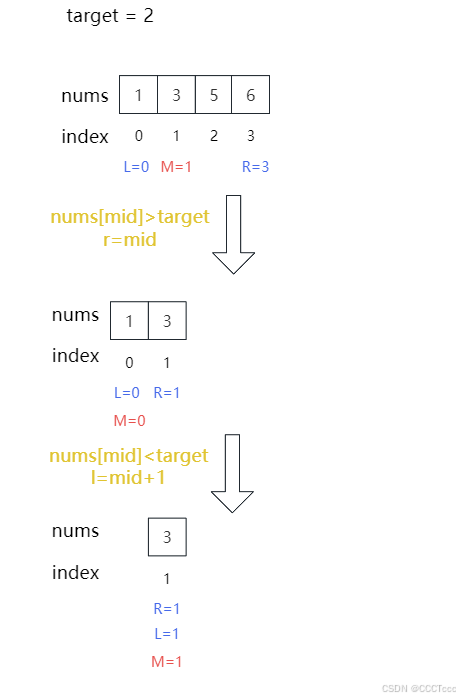
4.补充一题类似的：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l = 0, r = nums.size() - 1;
        while(l < r)
        {
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        //如果nums[l] > target，target要插入的位置就是l
        if(nums[l] >= target) return l;
        else return l + 1;
    }
};