【leetcode hot 100】（链表）141 判断链表是否有环 +142寻找环的入口

1.原题：

141.

142.
返回环的入口索引

2. 思路：

2.1判断链表是否有环

快慢指针法
fast slow，从头节点出发，fast指针每次移动2个节点，slow指针每次移动1个节点，如果fast指针和slow指针在途中相遇，说明这个链表有环。

如果有环，则fast指针和slow指针一定会相遇，因为fast移动两个节点，slow移动1一个节点，fast是以一个节点去靠近slow的，fast至少要移动一圈才能遇到slow(ps:代码随想录的动画很清晰)

2.2 环的入口

通过判断链表是否有环的图，可以知道fast至少要移动一圈才能遇到slow
要找到环的入口，可以说是找规律，转换成数学问题啦(参考代码随想录)

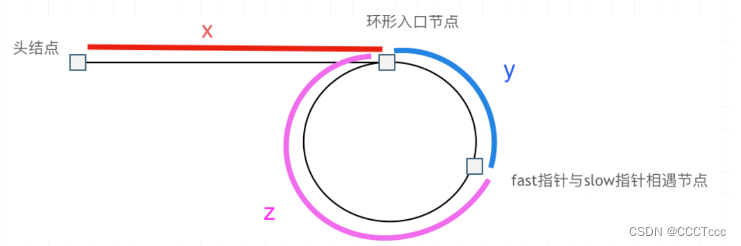
fast指针和slow指针相遇的时候

• slow 指针移动的节点数是 $x+y$
• fast 指针移动的节点数是$x+y+n(y+z)$，n的含义就是fast在环内移动了n圈才遇到slow指针
• slow跟fast移动的节点数存在了一定关系，fast指针移动的节点数是slow指针移动的节点数的2倍，所以得到：$(x+y)\times 2=x+y+n(y+z)$

因为要找环的入口，所以计算x，x整理后 $x=(n-1)(y+z)+z$

• 当n=1时，x=z
  • 意味着，一个指针从头节点出发，另一个指针从相遇节点出发，两个指针一起只移动一个节点，则两个指针相遇的节点就是环的入口节点
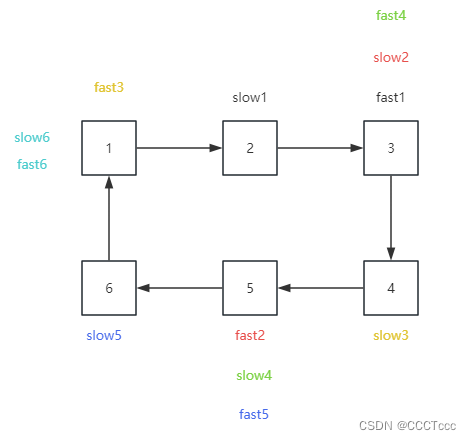
• 当n>1时
  • 意味着，fast指针在环中移动了n圈之后才遇到slow指针

3.代码

3.1 判断是否有环

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        //起码三个节点才能构成环
    //    if(head == NULL || head -> next == NULL)
    //    {
    //         return false;
    //    }
        
        ListNode *fast = head;
        ListNode *slow = head;

        while(fast != NULL && fast -> next != NULL)
        {

            slow = slow->next;
            fast = fast->next->next;

            if(fast == slow)
                return true;


        }
        return false;
    }
};

3.2 输出环的入口

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast = head;
        ListNode *slow = head;

        while(fast != NULL && fast->next != NULL)
        {
            fast = fast->next->next;
            slow = slow->next;

            if(fast == slow)
            {
                ListNode *index1 = fast;
                ListNode *index2 = head;

                while(index1 != index2)
                {
                    index1 = index1 -> next;
                    index2 = index2 -> next;
                }
                return index1;
            }

        }
        return NULL;
    }
};