Distance Tree 全网最丑做法

原创已于 2022-07-15 14:20:33 修改 · 305 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2022-07-14 22:23:39 首次发布

本文探讨了一种图论问题，涉及找到从根节点出发，经过新加入边的最大路径长度。通过建立不等式，作者推导出一个求解最大路径长度的公式，并利用二分查找来优化计算过程。文章还提供了C++实现的参考代码。

1.前言

为什么我总是一些正常人想不到的思路……

2.题解

首先有一个很显然的结论，连接的两个点一个为根节点，一个为以一为链顶的最长链上，记这个最长链的点集合为 $l$ 。

假设我们当前连边的长度为 $x$ ，连接到的点距离 $1$ 长 $y$ ，最短路经过新加入的边的点的集合为 $s$ ， $idx_i$ 表示 $i$ 向上的第一个在 $l$ 上的点距离 $1$ 的长度， $h_i$ 表示 $i$ 到向上的第一个在 $l$ 上的点的距离 , $mi d$ 表示答案。

用一张图形象的表示 $↓\downarrow$

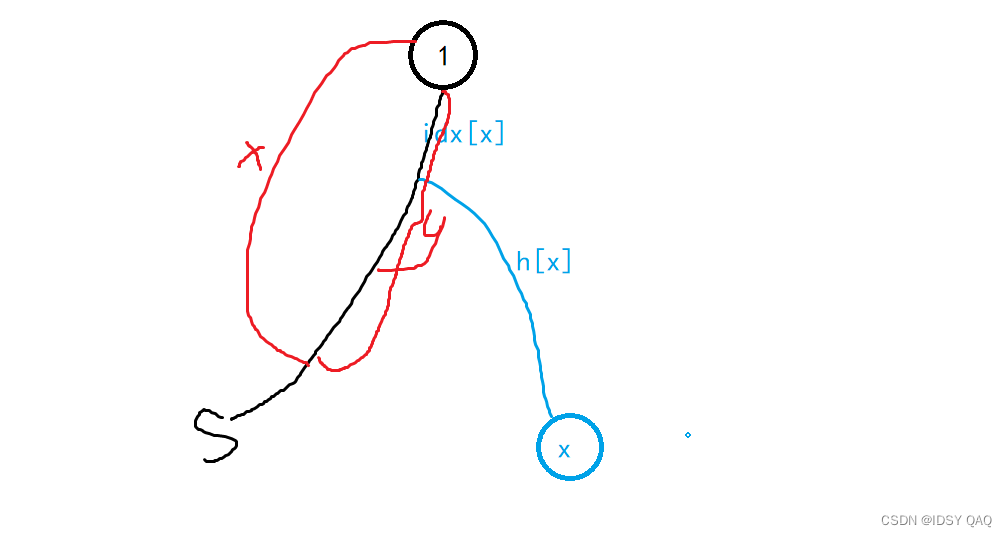
在这里插入图片描述

我们可以列出两个不等式
$\begin{aligned} \mid y - idx_i \mid + h_i + x \leq mid (i \in \mathbb{S}) \\ idx_i+h_i \leq mid (i \notin \mathbb{S}) \end{aligned}$

第二个不等式已经足够简洁，我们对第一个 $\in \mathbb{S}$ 的不等式进行化简。

$idx_i - (mid - x - h_i) \leq y \leq idx_i+ (mid - x - h_i)$

我们的要求就是

$∃y,idxi−(mid−x−hi)≤y≤idxi+(mid−x−hi)(i∈S)\exists y,idx_i - (mid - x - h_i) \leq y \leq idx_i+ (mid - x - h_i)(i \in \mathbb{S})$

什么情况满足呢？可以把它想成多个区间求交集后不为空集，即

$min⁡(idxi+(mid−x−hi)(i∈S))≥max⁡(idxi−(mid−x−hi))(i∈S))\min (idx_i+ (mid - x - h_i)(i \in \mathbb{S})) \geq \max (idx_i - (mid - x - h_i))(i \in \mathbb{S}))$

通过这个，我们反解出 $mi d$

$\geq \lceil \frac{2*x + \max (idx_i + h_i) - \min (idx_i - h_i)}{2} \rceil (i \in \mathbb{S})$

那么，我们可以得出 $mi d$ 的表达式

$max⁡(⌈2∗x+max⁡(idxi+hi)−min⁡(idxi−hi)2⌉(i∈S),idxi+hi(i∉S))\max (\lceil \frac{2*x + \max (idx_i + h_i) - \min (idx_i - h_i)}{2} \rceil (i \in \mathbb{S}), idx_i+h_i(i \notin \mathbb{S}))$

按照 $idx_i +h_i$ 排序，贪心容易知道，选择的 $S\mathbb{S}$ 集合在排序后的序列上一定是连续的，且左端点为 $1$ ，记 $S\mathbb{S}$ 的右端点为 $r$ 。

发现左边的式子随着 $r$ 的变大而变小。如果记左，右边的式子分别为函数 $f (r), g (r)$ ，则大概有这样一个函数图像 $↓\downarrow$ 。

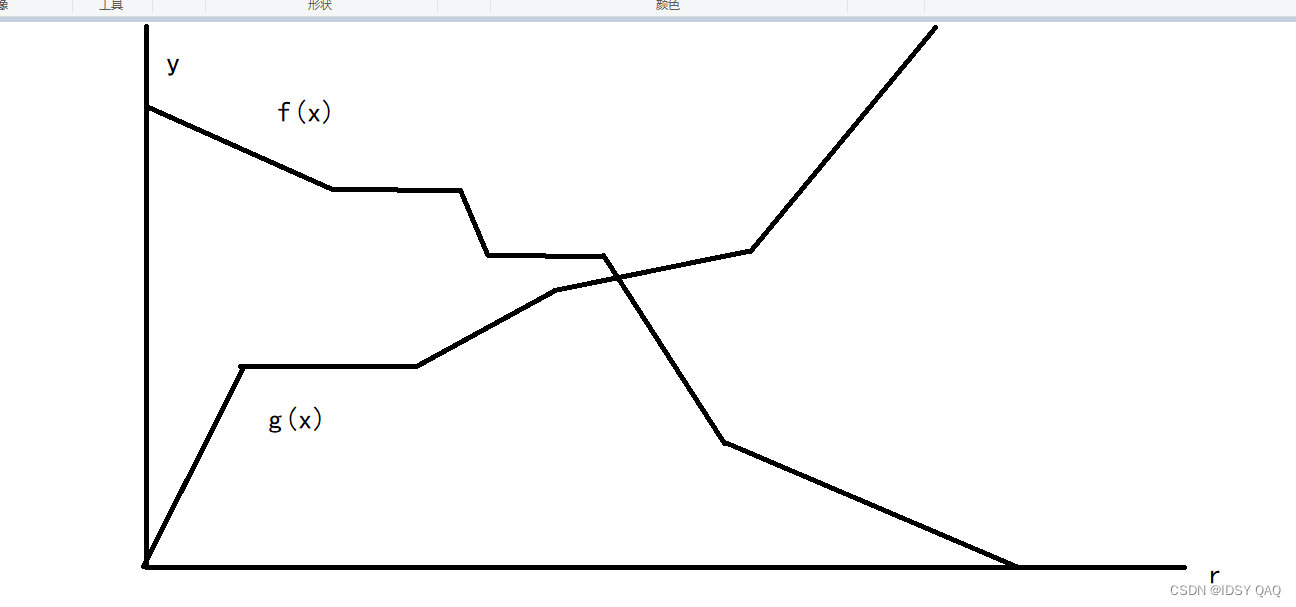
在这里插入图片描述
这个最大值函数的最小值即为 $f (x)$ 和 $g (x)$ 的交点 (因为 $\neq 0, f(0) \neq 0, f (n + 1) = 0$ ，以及 $f (x)$ 为单调不递增函数， $g (x)$ 为单调不递减函数，可以证明他们必有交点，且交点的函数值相等)，这是一个经典问题，二分 $max⁡(x)(f(x)≥g(x))\max (x) (f(x) \geq g(x))$ 即可。

参考代码

#include <set>
#include <map>
#include <cmath>
#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define int long long
#define PII pair <int, int>
#define ULL unsigned long long
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); i++)
#define per(i,j,k) for (int i = (j); i >= (k); i--)

template <typename T>
void read (T &x) {
    x = 0; T f = 1; 
    char ch = getchar ();
    while (ch < '0' || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar ();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + ch - '0';
        ch = getchar ();
    }
    x *= f;
}
template <typename T, typename... Args>
void read (T &x, Args&... Arg) {
    read (x), read (Arg...);
}
const int MaxPrint = 1000;
int Poi_For_Print, Tmp_For_Print[MaxPrint + 5];
template <typename T>
void write (T x) {
	if (x == 0) {
		putchar ('0');
		return;
	}
    bool flag = (x < 0 ? 1 : 0);
    x = (x < 0 ? -x : x);
    while (x) Tmp_For_Print[++Poi_For_Print] = x % 10, x /= 10;
    if (flag) putchar ('-');
    while (Poi_For_Print) putchar (Tmp_For_Print[Poi_For_Print--] + '0');
}
template <typename T, typename... Args>
void write (T x, Args... Arg) {
    write (x); putchar (' '); write (Arg...);
}
template <typename T, typename... Args>
void print (T x, char ch) {
    write (x); putchar (ch);
}
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }

const int Maxn = 3 * 1e5;
const int Inf = 0x3f3f3f3f3f3f3f;

int t, n;

vector <int> g[Maxn + 5];
void add (int x, int y) {
    g[x].push_back (y);
}

int dp[Maxn + 5], id[Maxn + 5], fa[Maxn + 5];
void Tree (int u, int _fa) {
    for (auto v : g[u]) {
        if (v == _fa) continue;
        fa[v] = u;
        Tree (v, u);
        if (dp[v] + 1 > dp[u]) {
            dp[u] = dp[v] + 1;
            id[u] = v;
        }
    }
}
int cnt, dist[Maxn + 5], _min[Maxn + 5], _max[Maxn + 5];
bool vis[Maxn + 5];
struct Node {
    int h, idx;
} a[Maxn + 5];
bool cmp (Node x, Node y) {
    return x.h + x.idx < y.h + y.idx;
}
int Query1 (int mid) {
	if (mid < 0 || mid > cnt) return Inf;
	if (mid == 0) return 0;
    return a[mid].idx + a[mid].h;
}
int Query2 (int mid, int x) {
	if (mid < 1 || mid > cnt + 1) return Inf;
	if (mid == cnt + 1) return 0;
    return (2 * x + _max[mid] - _min[mid] + 1) / 2;
}

signed main () {
//    freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.in", "r", stdin);
    // freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.out", "w", stdout);

    read (t);
    while (t--) {
        read (n);
        rep (i, 1, cnt) a[i].h = a[i].idx = 0; cnt = 0;
        rep (i, 1, n) g[i].clear (), dp[i] = 0, dist[i] = 0, vis[i] = 0;
        
        rep (i, 1, n - 1) {
            int x, y; read (x, y);
            add (x, y), add (y, x);
        }
        Tree (1, -1);
        int u, v, Now = 0; u = 1;
        do {
            v = u;
            u = id[u];
            vis[v] = 1;
            dist[v] = Now++;
        } while (g[v].size () != 1 || v == 1);
        rep (i, 2, n) {
        	if (vis[i]) {
        		cnt++;
        		a[cnt].h = 0;
        		a[cnt].idx = dist[i];
        		continue;
			}
            if (g[i].size () == 1) {
                cnt++;
                v = i;
                while (!vis[v]) {
                    a[cnt].h++;
                    v = fa[v];
                }
                a[cnt].idx = dist[v];
            }
        }
        sort (a + 1, a + 1 + cnt, cmp);
        
        _max[cnt + 1] = -Inf; _min[cnt + 1] = Inf;
        per (i, cnt, 1) {
            _max[i] = Max (_max[i + 1], a[i].idx + a[i].h);
            _min[i] = Min (_min[i + 1], a[i].idx - a[i].h);
        }
        rep (x, 1, n) {
            int l = -1, r = cnt + 2;
            while (l + 1 < r) {
                int mid = (l + r) >> 1;
                if (Query1 (mid) <= Query2 (mid + 1, x)) l = mid;
                else r = mid;
            }
            print (Min (Max (Query1 (l), Query2 (l + 1, x)), Max (Query1 (l + 1), Query2 (l + 2, x))), ' ');
        }
        putchar ('\n');
    }
    return 0;
}