本文详细解析了几道编程竞赛题目，包括题解思路、错误原因及修正后的代码。第一题涉及组合计数，挂分原因是大整数乘法未取模；第二题是数位DP问题，挂分原因为计算质因数幂次时忘记考虑正负；第三题是组合数学应用，挂分原因为负数阶乘处理不当；第四题是字符串处理，挂分原因为数组越界。修复后的代码已提供。
1.前言：
rt，准备回归 WHK 了
2.题解：
T1：
结论题，先猜后证。
结论：走一个直角最优。
证明：
由于整个图是关于对角线对称的，所以说我们走到 (n,m)(n, m)(n,m) 和 (m,n)(m, n)(m,n) 的最小结果是一样的，所以不妨使 n>mn > mn>m。
有个容易发现的性质
- 不走回头路（只向下和向右走）
考虑修改单步。
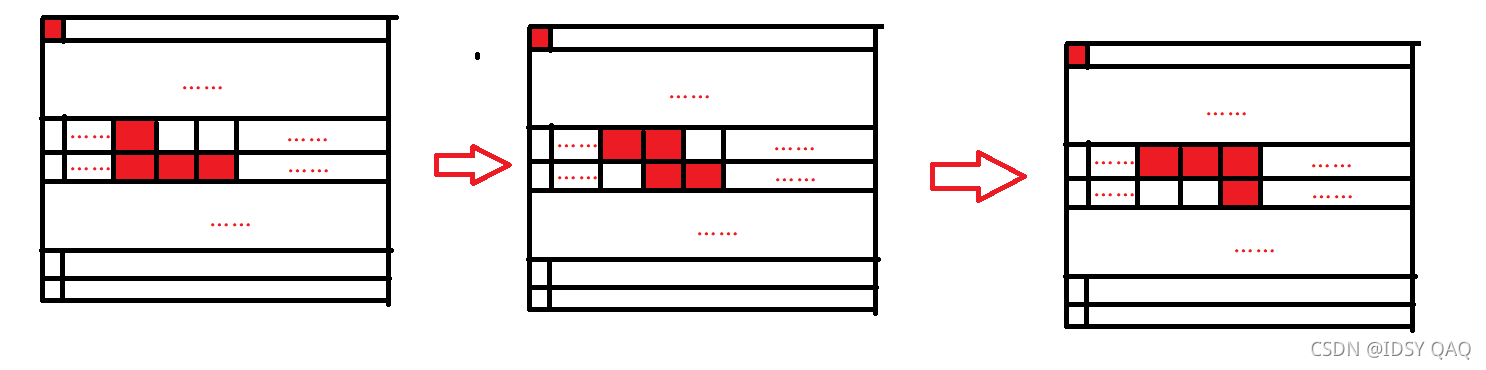
如果修改的步数都在对角线内，那么一定变大。
如果修改的步数都在对角线外，这种情况又不如图三。
这样递归到边线，得到某一条边线最短。容易知道靠下的边线最短，如下图。
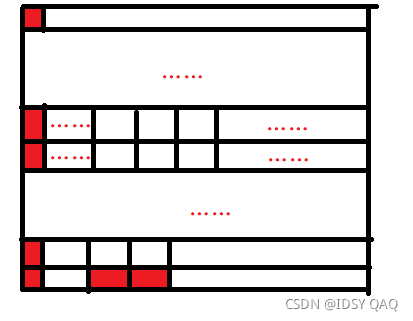
向下走的代价是 n+1n + 1n+1
向右走的代价是 ∑i=0m(n+in)=(n+m+1n+1)\sum_{i = 0}^{m} \binom {n + i}{n} = \binom{n + m + 1}{n + 1}∑i=0m(nn+i)=(n+1n+m+1)
交叉点被算了两次，所以总代价是 (n+m+1n+1)+n\binom{n + m + 1}{n + 1} + n(n+1n+m+1)+n
n,mn, mn,m 很大，考虑怎么求解组合数。
(n+m+1n+1)=(n+m+1m)\binom{n + m + 1}{n + 1} = \binom{n + m + 1}{m}(n+1n+m+1)=(mn+m+1)
所以我们找到 n+1,mn + 1, mn+1,m 中的最小值，然后用 (ab)=a!b!(a−b)!=Πi=a−b+1aib!\binom{a}{b} = \frac{a!}{b!(a - b)!} = \frac{\Pi_{i = a - b + 1}^{a} i}{ b!}(ba)=b!(a−b)!a!=b!Πi=a−b+1ai 即可。
时间复杂度分析， n×m=1e12n \times m = 1e12n×m=1e12 则 min(n,m)max=sqrt(1e12)=1e6\min (n, m)_{max} = sqrt (1e12) = 1e6min(n,m)max=sqrt(1e12)=1e6，所以时间复杂度为 O(1e6)O(1e6)O(1e6)
挂分原因：iii 很大，没有先取模，于是 i∗resi * resi∗res 就挂了……
T2:
题意转换：相当于用所有非零的数和任意个零组成的小于 nnn 的个数（位数不够用前导零）。（不过我考场时讨论了数的长度，也是一样的道理）
类似于数位dp，枚举到了第 iii 位，前 i−1i - 1i−1 位都相同，枚举这一位选的数 (a[i]a[i]a[i])，如果这一位小于 n[i]n[i]n[i] ，那么后面怎么选都可以了，如果相同，则 a[(i+1)a[(i + 1)a[(i+1) ~ n]n]n] 一定要小于 n[(i+1)n[(i + 1)n[(i+1)~n]n]n]，这就交给后面的 iii 了。
挂分原因：
- 求质因数的幂次时忘记乘上 opopop, 就没有区别分子和分母对幂次贡献的正负了……
- pi=pi−1∗p=tmp∗pp ^ i = p ^ {i - 1} * p = tmp * ppi=pi−1∗p=tmp∗p，不是 tmp∗tmptmp * tmptmp∗tmp 啊！！！！！
这个东西却让我把样例和我手玩数据都对了。（样例无语，但是手玩数据时我为了偷懒，只搞了多个零然后其他数字都不一样的数据，所以没测出来。）
T3：
板题，枚举有几个字符的大小超过了 n−1n - 1n−1， 容斥即可。
假设现在有 iii 个数超过了 n−1n - 1n−1，那么方案数就为
- 选出 iii 个数，让他们一定超过 n−1n - 1n−1，方案数为 (mi)\binom{m}{i}(im)
- 那么此时让这几个数都减去 nnn，那么这时所有数加起来为 k−n∗ik - n * ik−n∗i，所以方案数为 Fk−n∗im=(k−n∗i+m−1m−1)F_{k - n * i}^{m} = \binom{k - n * i + m - 1}{m - 1}Fk−n∗im=(m−1k−n∗i+m−1)。
- 系数为 (−1)i(-1)^i(−1)i
乘法原理，这个 iii 的贡献为： (−1)i(k−n∗i+m−1m−1)(mi)(-1)^i\binom{k - n * i + m - 1}{m - 1} \binom{m}{i}(−1)i(m−1k−n∗i+m−1)(im)
ans=∑i=0m(−1)i(k−n∗i+m−1m−1)(mi)ans = \sum_{i = 0}^{m} (-1)^i\binom{k - n * i + m - 1}{m - 1} \binom{m}{i}ans=∑i=0m(−1)i(m−1k−n∗i+m−1)(im)
挂分原因：如果 k−n∗i+m−1<m−1k - n * i + m - 1 < m - 1k−n∗i+m−1<m−1 就会出现负数的阶乘，没有特判啊。
本机数组下标小于零的话，他聪明的给我搞了个零而不是卡住，笑死。
T4:
板题。
容斥，考虑这个人有多少人和他不是敌对关系。
加上和 iii 第{1},{2},{3},{4},{5}爱好相同的人
减去和 iii 第{1,2},{1,3},{1,4},{1,5},{2,3}…爱好相同的人。
…
把这些爱好的值用桶记录即可。
这里也可以用 Trie+HashTrie + HashTrie+Hash 的做法。(卡常数）
HashHashHash 作用有两个：
- 将一个人的爱好子集搞成一个 ULL
- HashHashHash 找到 ppp 节点的 chchch 这个儿子的下标
TrieTrieTrie 就是模板了
挂分原因：卡常数……
3.考场源码及挂分点标注。
T1:
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define ULL unsigned long long
#define PII pair <int, int>
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); ++i)
#define per(i,j,k) for (int i = (j); i >= (k); --i)
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
char For_Print[25];
template <typename T>
void write (T x) {
if (x == 0) { putchar ('0'); return; }
if (x < 0) { putchar ('-'); x = -x; }
int poi = 0;
while (x) {
For_Print[++poi] = x % 10 + '0';
x /= 10;
}
while (poi) putchar (For_Print[poi--]);
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
const LL Mod = 1e9 + 7;
const LL Limit = 2 * 1e6;
LL n, m;
LL inv[Limit + 5];
void del (LL &x, LL y) { ((x -= y) < 0) && (x += Mod); }
void add (LL &x, LL y) { ((x += y) >= Mod) && (x -= Mod); }
LL C (LL x, LL y) {
if (y > Limit) y = x - y;
LL res = 1;
for (LL i = x; i > x - y; i--) res = (res * i /* 就是这里！！！！！！！*/) % Mod;
for (LL i = y; i > 0; i--) res = (res * inv[i]) % Mod;
return res;
}
int main () {
freopen ("jump.in", "r", stdin);
freopen ("jump.out", "w", stdout);
inv[1] = 1; rep (i, 2, Limit) inv[i] = (Mod - Mod / i) * inv[Mod % i] % Mod;
read (n); read (m);
if (n < m) swap (n, m);
write ((n + C (m + n + 1, n + 1)) % Mod);
return 0;
}
T2
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define ULL unsigned long long
#define PII pair <int, int>
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); ++i)
#define per(i,j,k) for (int i = (j); i >= (k); --i)
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
char For_Print[25];
template <typename T>
void write (T x) {
if (x == 0) { putchar ('0'); return; }
if (x < 0) { putchar ('-'); x = -x; }
int poi = 0;
while (x) {
For_Print[++poi] = x % 10 + '0';
x /= 10;
}
while (poi) putchar (For_Print[poi--]);
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
const int Maxn = 200;
int lenn, lenm;
char n[Maxn + 5], m[Maxn + 5];
int bak[Maxn + 5];
int cnt, primes[Maxn + 5];
bool vis[Maxn + 5];
void Euler () {
rep (i, 2, Maxn) {
if (vis[i] == 0) {
vis[i] = 1;
primes[++cnt] = i;
}
rep (j, 1, cnt) {
if (primes[j] > Maxn / i) break;
vis[i * primes[j]] = 1;
if (i % primes[j] == 0) break;
}
}
}
int tot[Maxn + 5];
ULL quick_pow (ULL x, int y) {
ULL res = 1;
while (y) {
if (y & 1) res = res * x;
x = x * x; y >>= 1;
}
return res;
}
void Calc (int x, int op) {
rep (i, 1, cnt) {
int tmp = primes[i];
while (tmp <= x) {
tot[i] += x / tmp /* 我的 "*op" 呢？？？？ */;
tmp *= tmp; /* tmp应该 *= primes[i]啊！！！ */
}
}
}
ULL Get_Res () {
ULL res = 1;
memset (tot, 0, sizeof tot);
int sum = 0;
rep (j, 0, 9) { Calc (bak[j], -1); sum += bak[j]; }
Calc (sum, 1);
rep (j, 1, cnt) res *= quick_pow (primes[j], tot[j]);
return res;
}
ULL fac[Maxn + 5];
int main () {
// freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.in", "r", stdin);
// freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.out", "w", stdout);
freopen ("count.in", "r", stdin);
freopen ("count.out", "w", stdout);
fac[1] = 1; rep (i, 2, Maxn) fac[i] = fac[i - 1] * i;
Euler ();
scanf ("%s", n + 1);
lenn = strlen (n + 1);
rep (i, 1, lenn)
if (n[i] != '0')
m[++lenm] = n[i];
ULL ans = 0;
//数位小于 n
rep (i, 1, lenm) bak[m[i] - '0']++;
/*
rep (i, 0, lenn - lenm - 1) {
ULL res1 = 0, res2 = 0;
bak[0] = i;
res1 = Get_Res ();
if (i != 0) {
bak[0] = i - 1;
res2 = Get_Res ();
}
ans += res1 - res2;
}
*/
// /*
if (lenn - lenm - 1 >= 0) {
bak[0] = lenn - lenm - 1;
ans += Get_Res ();
}
// */
// 数位等于 n
bak[0] = lenn - lenm;
rep (i, 1, lenn) {
rep (j, 0, n[i] - '0' - 1) {
if (!bak[j]) continue;
if (i == 1 && j == 0) continue;
bak[j]--;
ans += Get_Res ();
bak[j]++;
}
bak[n[i] - '0']--;
}
write (ans);
return 0;
}
T3:
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define ULL unsigned long long
#define PII pair <int, int>
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); ++i)
#define per(i,j,k) for (int i = (j); i >= (k); --i)
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
char For_Print[25];
template <typename T>
void write (T x) {
if (x == 0) { putchar ('0'); return; }
if (x < 0) { putchar ('-'); x = -x; }
int poi = 0;
while (x) {
For_Print[++poi] = x % 10 + '0';
x /= 10;
}
while (poi) putchar (For_Print[poi--]);
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
const int Maxn = 2 * 1e5;
const LL Mod = 998244353;
void del (LL &x, LL y) { ((x -= y) < 0) && (x += Mod); }
void add (LL &x, LL y) { ((x += y) >= Mod) && (x -= Mod); }
int t, n, m, k;
LL fac[Maxn + 5], inv_fac[Maxn + 5];
LL quick_pow (LL x, LL y) {
LL res = 1;
while (y) {
if (y & 1) res = (res * x) % Mod;
x = (x * x) % Mod; y >>= 1;
}
return res;
}
LL inv (LL x) {
return quick_pow (x, Mod - 2);
}
LL C (LL x, LL y) {
if (x < 0 || y < 0) return 0; //x - y < 0 怎么办？？？？
if (y == 0 || y == x) return 1;
return fac[x] * inv_fac[y] % Mod * inv_fac[x - y] % Mod;
}
int main () {
freopen ("encoding.in", "r", stdin);
freopen ("encoding.out", "w", stdout);
fac[1] = 1; rep (i, 2, Maxn) fac[i] = fac[i - 1] * i % Mod;
inv_fac[Maxn] = inv (fac[Maxn]); per (i, Maxn - 1, 1) inv_fac[i] = inv_fac[i + 1] * (i + 1) % Mod;
read (t);
while (t--) {
read (n); read (m); read (k);
LL res = 0;
rep (i, 0, m) {
if (i & 1) del (res, C (k - i * n + m - 1, m - 1) * C (m, i) % Mod);
else add (res, C (k - i * n + m - 1, m - 1) * C (m, i) % Mod);
}
print (res, '\n');
}
return 0;
}
#include <map>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define ULL unsigned long long
#define PII pair <int, int>
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); ++i)
#define per(i,j,k) for (int i = (j); i >= (k); --i)
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
char For_Print[25];
template <typename T>
void write (T x) {
if (x == 0) { putchar ('0'); return; }
if (x < 0) { putchar ('-'); x = -x; }
int poi = 0;
while (x) {
For_Print[++poi] = x % 10 + '0';
x /= 10;
}
while (poi) putchar (For_Print[poi--]);
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
const int Maxn = 5 * 1e4;
const int Maxm = 5;
const ULL P = 1333331;
int n, m = 5;
int a[Maxn + 5][Maxm + 5];
map <ULL, int> bak;
int main () {
// freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.in", "r", stdin);
// freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.out", "w", stdout);
freopen ("against.in", "r", stdin);
freopen ("against.out", "w", stdout);
read (n);
LL res = 0;
rep (i, 1, n) {
rep (j, 1, m) {
read (a[i][j]);
// if (a[i][j] == 0) printf ("FUCK");
}
sort (a[i] + 1, a[i] + 1 + m);
rep (j, 1, (1 << m) - 1) {
int sum = 0; ULL tmp = 0;
rep (k, 1, m) {
if ((j >> (k - 1)) & 1) {
tmp = tmp * P + a[i][k];
sum++;
}
}
if (bak.find (tmp) == bak.end ()) bak[tmp] = 0;
bak[tmp]++;
if (sum & 1) {
res = res + (bak[tmp] - 1);
}
else {
res = res - (bak[tmp] - 1);
}
// printf ("i = %d, j = %d, res = %lld\n", i, j, res);
}
}
write ((LL)n * (n - 1) / 2 - res);
return 0;
}
4.考场改后代码
T1:
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define ULL unsigned long long
#define PII pair <int, int>
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); ++i)
#define per(i,j,k) for (int i = (j); i >= (k); --i)
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
char For_Print[25];
template <typename T>
void write (T x) {
if (x == 0) { putchar ('0'); return; }
if (x < 0) { putchar ('-'); x = -x; }
int poi = 0;
while (x) {
For_Print[++poi] = x % 10 + '0';
x /= 10;
}
while (poi) putchar (For_Print[poi--]);
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
const LL Mod = 1e9 + 7;
const LL Limit = 2 * 1e6;
LL n, m;
LL inv[Limit + 5];
void del (LL &x, LL y) { ((x -= y) < 0) && (x += Mod); }
void add (LL &x, LL y) { ((x += y) >= Mod) && (x -= Mod); }
LL C (LL x, LL y) {
if (y > Limit) y = x - y;
LL res = 1;
for (LL i = x; i > x - y; i--) res = (res * (i % Mod)) % Mod;
for (LL i = y; i > 0; i--) res = (res * inv[i]) % Mod;
return res;
}
int main () {
freopen ("jump.in", "r", stdin);
freopen ("jump.out", "w", stdout);
inv[1] = 1; rep (i, 2, Limit) inv[i] = (Mod - Mod / i) * inv[Mod % i] % Mod;
read (n); read (m);
if (n < m) swap (n, m);
write ((n + C (m + n + 1, n + 1)) % Mod);
return 0;
}
T2:
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define ULL unsigned long long
#define PII pair <int, int>
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); ++i)
#define per(i,j,k) for (int i = (j); i >= (k); --i)
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
char For_Print[25];
template <typename T>
void write (T x) {
if (x == 0) { putchar ('0'); return; }
if (x < 0) { putchar ('-'); x = -x; }
int poi = 0;
while (x) {
For_Print[++poi] = x % 10 + '0';
x /= 10;
}
while (poi) putchar (For_Print[poi--]);
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
const int Maxn = 200;
int lenn, lenm;
char n[Maxn + 5], m[Maxn + 5];
int bak[Maxn + 5];
int cnt, primes[Maxn + 5];
bool vis[Maxn + 5];
void Euler () {
rep (i, 2, Maxn) {
if (vis[i] == 0) {
vis[i] = 1;
primes[++cnt] = i;
}
rep (j, 1, cnt) {
if (primes[j] > Maxn / i) break;
vis[i * primes[j]] = 1;
if (i % primes[j] == 0) break;
}
}
}
int tot[Maxn + 5];
ULL quick_pow (ULL x, int y) {
ULL res = 1;
while (y) {
if (y & 1) res = res * x;
x = x * x; y >>= 1;
}
return res;
}
void Calc (int x, int op) {
rep (i, 1, cnt) {
int tmp = primes[i];
while (tmp <= x) {
tot[i] += (x / tmp) * op;
tmp *= primes[i];
}
}
}
ULL Get_Res () {
ULL res = 1;
memset (tot, 0, sizeof tot);
int sum = 0;
rep (j, 0, 9) { Calc (bak[j], -1); sum += bak[j]; }
Calc (sum, 1);
rep (j, 1, cnt) res *= quick_pow (primes[j], tot[j]);
return res;
}
ULL fac[Maxn + 5];
int main () {
// freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.in", "r", stdin);
// freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.out", "w", stdout);
freopen ("count.in", "r", stdin);
freopen ("count.out", "w", stdout);
fac[1] = 1; rep (i, 2, Maxn) fac[i] = fac[i - 1] * i;
Euler ();
scanf ("%s", n + 1);
lenn = strlen (n + 1);
rep (i, 1, lenn)
if (n[i] != '0')
m[++lenm] = n[i];
ULL ans = 0;
//数位小于 n
rep (i, 1, lenm) bak[m[i] - '0']++;
/*
rep (i, 0, lenn - lenm - 1) {
ULL res1 = 0, res2 = 0;
bak[0] = i;
res1 = Get_Res ();
if (i != 0) {
bak[0] = i - 1;
res2 = Get_Res ();
}
ans += res1 - res2;
}
*/
// /*
if (lenn - lenm - 1 >= 0) {
bak[0] = lenn - lenm - 1;
ans += Get_Res ();
}
else {
bak[0] = 0;
}
// */
// 数位等于 n
bak[0] = lenn - lenm;
rep (i, 1, lenn) {
rep (j, 0, n[i] - '0' - 1) {
if (!bak[j]) continue;
if (i == 1 && j == 0) continue;
bak[j]--;
ans += Get_Res ();
bak[j]++;
}
bak[n[i] - '0']--;
}
write (ans);
return 0;
}
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define ULL unsigned long long
#define PII pair <int, int>
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); ++i)
#define per(i,j,k) for (int i = (j); i >= (k); --i)
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
char For_Print[25];
template <typename T>
void write (T x) {
if (x == 0) { putchar ('0'); return; }
if (x < 0) { putchar ('-'); x = -x; }
int poi = 0;
while (x) {
For_Print[++poi] = x % 10 + '0';
x /= 10;
}
while (poi) putchar (For_Print[poi--]);
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
const int Maxn = 3 * 1e5;
const LL Mod = 998244353;
void del (LL &x, LL y) { ((x -= y) < 0) && (x += Mod); }
void add (LL &x, LL y) { ((x += y) >= Mod) && (x -= Mod); }
int t; LL n, m, k;
LL fac[Maxn + 5], inv_fac[Maxn + 5];
LL quick_pow (LL x, LL y) {
LL res = 1;
while (y) {
if (y & 1) res = (res * x) % Mod;
x = (x * x) % Mod; y >>= 1;
}
return res;
}
LL inv (LL x) {
return quick_pow (x, Mod - 2);
}
LL C (LL x, LL y) {
if (x < 0 || y < 0) return 0;
if (y == 0 || y == x) return 1;
if (x - y < 0) return 0;
return fac[x] * inv_fac[y] % Mod * inv_fac[x - y] % Mod;
}
int main () {
freopen ("encoding.in", "r", stdin);
freopen ("encoding.out", "w", stdout);
fac[1] = 1; rep (i, 2, Maxn) fac[i] = fac[i - 1] * i % Mod;
inv_fac[Maxn] = inv (fac[Maxn]); per (i, Maxn - 1, 1) inv_fac[i] = inv_fac[i + 1] * (i + 1) % Mod;
read (t);
while (t--) {
read (n); read (m); read (k);
LL res = 0;
rep (i, 0, m) {
if (i & 1) del (res, C (k - i * n + m - 1, m - 1) * C (m, i) % Mod);
else add (res, C (k - i * n + m - 1, m - 1) * C (m, i) % Mod);
}
print (res, '\n');
}
return 0;
}
T4:
#include <map>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define fi first
#define se second
#define db double
#define LL long long
#define ULL unsigned int
#define PII pair <int, int>
#define MP(x,y) make_pair (x, y)
#define rep(i,j,k) for (int i = (j); i <= (k); ++i)
#define per(i,j,k) for (int i = (j); i >= (k); --i)
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
char For_Print[25];
template <typename T>
void write (T x) {
if (x == 0) { putchar ('0'); return; }
if (x < 0) { putchar ('-'); x = -x; }
int poi = 0;
while (x) {
For_Print[++poi] = x % 10 + '0';
x /= 10;
}
while (poi) putchar (For_Print[poi--]);
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
const int Maxn = 5 * 1e4;
const int Maxm = 5;
const int Maxt = 1e7;
const int MaxTire = 114514;
const ULL P = 133331;
int n, m = 5;
int a[Maxn + 5][Maxm + 5];
int cnt, len, x[Maxm + 5];
int End[Maxt + 5];
struct Node {
int p, ch, to;
Node () {}
Node (int _p, int _ch, int _to) {
p = _p; ch = _ch; to = _to;
}
};
bool operator == (Node x, Node y) {
return (x.p == y.p) && (x.ch == y.ch);
}
vector <Node> Tire[MaxTire + 5];
int Find (int p, int ch) {
int Hash = (p * P + ch) % MaxTire;
// if (Tire[Hash].size () > 10000)
// printf ("A Tire[Hash].size () = %d\n", (int)Tire[Hash].size ());
for (int i = 0; i < (int)Tire[Hash].size (); i++) {
if (Tire[Hash][i] == Node (p, ch, -1))
return Tire[Hash][i].to;
}
return -1;
}
int Insert (int p, int ch) {
int Hash = (p * P + ch) % MaxTire;
// if (Tire[Hash].size () > 10000)
// printf ("B Tire[Hash].size () = %d\n", (int)Tire[Hash].size ());
Tire[Hash].push_back (Node (p, ch, ++cnt));
// if (Tire[Hash].size () > 10000)
// printf ("C Tire[Hash].size () = %d\n", (int)Tire[Hash].size ());
return cnt;
}
void Update () {
int p = 0;
rep (i, 1, len) {
int ch = x[i];
int to = Find (p, ch);
if (to == -1) to = Insert (p, ch);
p = to;
}
// printf ("cnt = %d\n", cnt);
End[p]++;
}
int Query () {
int p = 0;
rep (i, 1, len) {
int ch = x[i];
int to = Find (p, ch);
if (to == -1) return 0;
p = to;
}
return End[p];
}
int main () {
// freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.in", "r", stdin);
// freopen ("C:\\Users\\Administrator\\Desktop\\lihan\\1.out", "w", stdout);
freopen ("against.in", "r", stdin);
freopen ("against.out", "w", stdout);
read (n);
LL res = 0;
rep (i, 1, n) {
rep (j, 1, m) {
read (a[i][j]);
// if (a[i][j] == 0) printf ("FUCK");
}
sort (a[i] + 1, a[i] + 1 + m);
rep (j, 1, (1 << m) - 1) {
len = 0; memset (x, 0, sizeof x);
rep (k, 1, m) {
if ((j >> (k - 1)) & 1) {
x[++len] = a[i][k];
}
}
Update ();
if (len & 1) {
res = res + (Query () - 1);
}
else {
res = res - (Query () - 1);
}
}
}
write ((LL)n * (n - 1) / 2 - res);
return 0;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
