矩阵游戏

前言

我太菜了。。不得不看 TJ ，由于自己的 SB 誓言，我又来写 TJ 了。

蓝题我都要看 TJ， 我好菜啊，提前 AFO 吧

题解

题面

我们可以研究一个样例

.in

1
3
1 0 0
0 1 1
1 0 0

.out

No

我们做出这个操作，当 $a[i][j]=1$ 时，在二元组边集 $E$ 中加入一个元素 $(i,j)$，如图。

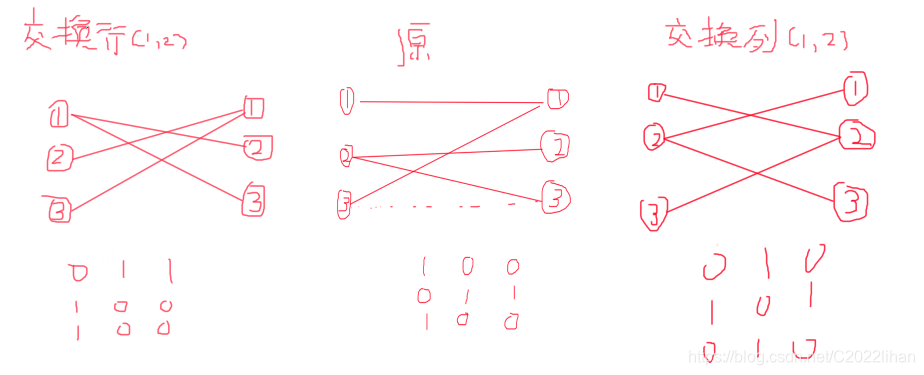
注:左边的表示行，右边的表示列。

若交换行

引理一：行的交换不会改变最大匹配数

若我们此时将行1和2的编号交换，我们会发现图又变成了原图，所以我们可以把行的交换理解成行编号的交换，所以不会改变最大匹配数。

引理二：当最大匹配数等于 $n$ 时，即匹配成功

而目标图像要求行$i$和列$i$匹配，而我们可以利用交换编号使其成为任意一个只要求点与点一一匹配的图像。

所以：

由引理一，我们的最大匹配数固定。再由引理二可知：

若初始图的最大匹配数不为 $n$，则无论怎么交换都不会变换成目标图像。

若初始图的最大匹配数为 $n$，则一定能变成目标图像。

若交换列

同理，根据图分析易得和交换行一样的结论

参考代码

#include <map>
#include <set>
#include <cmath>
#include <stack>
#include <queue>
#