雅礼集训 Day5 T2 sequence

最新推荐文章于 2019-04-04 18:26:51 发布

Master.Yi

最新推荐文章于 2019-04-04 18:26:51 发布

阅读量281

点赞数 1

CC 4.0 BY-SA版权

分类专栏：线段树

本文链接：https://blog.youkuaiyun.com/C20181220_xiang_m_y/article/details/86312155

线段树专栏收录该内容

19 篇文章

订阅专栏

本文介绍了一种利用线段树优化处理k好序列查询的方法，通过将询问按右端点排序，并使用vector记录关键变化点，实现区间修改与查询，最终达到O((n+q)logn)的时间复杂度。

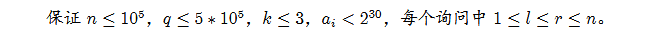
在这里插入图片描述

题目分析:

直接在线查询显然不好处理，那么我们把询问按照右端点排序，再从左至右枚举右端点，将以当前点为右端点的k好序列的左端点值+1，查询的时候只需要统计l到r的和就行了

但是暴力加1是O(n²)的，分析一下，以当前点为右端点的序列的按位与值在左端点变化时最多只会变化log次，那么把这log个变化点找出来，如果被k整除就在这个点和下一个变化点之间区间+1

那么就是区间修改+区间查询，线段树维护

找变化点的时候用vector很方便，每次把vector里的元素并上ai，再剔除掉相等的就好了，vector里的元素个数最多只有log个，所以整个算法的时间是O((n+q)logn)

#include<cstdio>
#include<vector>
#include<cctype>
#define maxn 100005
#define LL long long
#define pb(x) push_back(x)
using namespace std;
inline void read(int &a){char c;while(!isdigit(c=getchar()));for(a=c-'0';isdigit(c=getchar());a=a*10+c-'0');}
inline void write(LL a){if(a>=10) write(a/10);putchar(a%10+48);}
int n,m,k,a[maxn];
LL ans[5*maxn];
struct node{int id,x;node(int _id,int _x){id=_id,x=_x;}};
vector<node>Q[maxn],V,tmp;
struct Tree
{
	LL s[maxn<<2],laz[maxn<<2];
	void add(int i,int l,int r,int x){s[i]+=1ll*(r-l+1)*x,laz[i]+=x;}
	void pushdown(int i,int l,int r)
	{
		if(!laz[i]) return;
		int mid=(l+r)>>1;
		add(i<<1,l,mid,laz[i]);
		add(i<<1|1,mid+1,r,laz[i]);
		laz[i]=0;
	}
	void insert(int i,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y){
			add(i,l,r,1);
			return;
		}
		pushdown(i,l,r);
		int mid=(l+r)>>1;
		if(x<=mid) insert(i<<1,l,mid,x,y);
		if(y>mid) insert(i<<1|1,mid+1,r,x,y);
		s[i]=s[i<<1]+s[i<<1|1];
	}
	LL query(int i,int l,int r,int x,int y)
	{
		if(x<=l&&r<=y) return s[i];
		pushdown(i,l,r);
		int mid=(l+r)>>1;
		if(y<=mid) return query(i<<1,l,mid,x,y);
		if(x>mid) return query(i<<1|1,mid+1,r,x,y);
		else return query(i<<1,l,mid,x,y)+query(i<<1|1,mid+1,r,x,y);
	}
}T;
int main()
{
	freopen("sequence.in","r",stdin);
	freopen("sequence.out","w",stdout);
	read(n),read(m),read(k);
	for(int i=1;i<=n;i++) read(a[i]);
	for(int i=1,x,y;i<=m;i++) read(x),read(y),Q[y].pb(node(i,x));
	for(int i=1;i<=n;i++)
	{
		for(int j=V.size()-1;j>=0;j--) V[j].x&=a[i];
		V.pb(node(i,a[i]));
		tmp.clear();tmp.pb(V[0]);
		for(int j=1;j<V.size();j++) if(V[j].x!=V[j-1].x) tmp.pb(V[j]);
		V.swap(tmp);
		for(int j=0;j<V.size()-1;j++) if(V[j].x%k==0) T.insert(1,1,n,V[j].id,V[j+1].id-1);
		int j=V.size()-1;if(V[j].x%k==0) T.insert(1,1,n,V[j].id,i);

		for(int j=Q[i].size()-1;j>=0;j--) ans[Q[i][j].id]=T.query(1,1,n,Q[i][j].x,i);
	}
	for(int i=1;i<=m;i++) write(ans[i]),putchar('\n');
}