洛必达法则在解决不定式极限问题时十分有用，但也存在三大陷阱。一是要求右侧极限存在，否则需寻找其他方法；二是每次使用时都需确认是否仍为0/0或无穷/无穷形式；三是求导后需简化函数，避免复杂化。虽然洛必达法则有时繁琐，但泰勒级数可以作为替代工具，尤其在洛必达失效时。掌握使用条件并警惕陷阱，能更有效地运用洛必达法则。
洛必达法则是个好法则，我们都很喜欢用它，但稍不注意可能就落入陷阱了，尤其是考研的同学，出题老师可能会故意在细节上考察大家。所以本篇讲一下洛必达法则3大陷阱，提防着点总是好的！
1.洛必达法则内容：
2.粗略证明
注意：不是严谨证明，主要理解思路，严格证明用柯西中值定理，大家去看书。
从0/0型讲起，
无穷/无穷型我就不写了，因为你知道了0/0型，将分子分母颠倒便可用同样的道理得到相同结论了。
3.陷阱
利用洛必达法则注意以下陷阱：
3.1要求右侧极限存在
洛必达使用逻辑是有点诡异的，右侧极限存在，回推原极限存在，注意这里的存在包括无穷。那么不存在的情况，我们目前接触的应该是震荡的情况，需要找其他方法，通常比洛必达还要简单。举例：
3.2时刻检查是否满足0/0或无穷/无穷
通常用洛必达法则，第一步大家使用的时候，应该都会check是否满足条件，但是多次使用洛必达的时候一定注意别忘了check。
举例：
3.3求导后函数要简化
有些函数求导后会更加复杂，或者我们在选取分子分母的时候要比较细心，如果发现很难算，一定记得回头，调换分子分母试一下或者另谋它法。
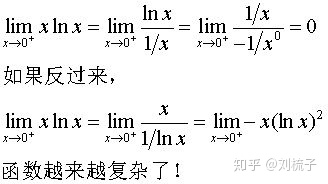
注意使用条件和这些陷阱的话，洛必达法则还是很好用的。
也有网友建议：
洛必达有啥好的…用前还要判断适用条件…烦死了烦死了…
还不如无脑上泰勒…凡是洛必达能解的，泰勒必定能解，洛必达失效时
泰勒还是能用…
没有什么题是一发三阶泰勒搞不定的，如果有，那就五阶…
扫一扫
5万+
到【灌水乐园】发言
