[BZOJ4766]文艺计算姬（矩阵+矩阵树定理+快速加）

最新推荐文章于 2021-07-03 18:26:28 发布

原创最新推荐文章于 2021-07-03 18:26:28 发布 · 557 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵 #矩阵树定理 #快速加

矩阵同时被 2 个专栏收录

15 篇文章

订阅专栏

矩阵树定理

6 篇文章

订阅专栏

本文详细解析了完全二分图的概念，并通过分块矩阵的行列式计算方法，介绍了如何利用快速乘和快速幂来解决相关问题。文章还提供了具体的代码实现。

题目：

我是超链接

题解：

完全二分图：X中的任一顶点与Y中每一个顶点均有且仅有唯一的一条边相连
不难发现K矩阵是长这个样子的
这里写图片描述
我们对这个矩阵分一下块，左上角是n * n的对角线为m的矩阵A，右上角是全为-1的n * (m-1)的矩阵B，左下角是全为-1的(m-1) * n的矩阵C，右下角是对角线为n的(m-1)*(m-1)的矩阵设为D

分块矩阵的行列式求法：
　
A 0
0 B
行列式为|A||B|
　
0 A
B 0
行列式为(-1)^(mn)|A||B|
　
A B
C D
行列式为|A||D-C*A^(-1)*B|

这个矩阵的|A|显然是m^n
后面 $A^{-1}$ 为A的逆矩阵，是一个主对角线为1/m，其余值为0的矩阵

逆矩阵：A的逆矩阵为与A相乘得单位矩阵的矩阵
单位矩阵：主对角线为1，其余为0的矩阵
可逆矩阵：有逆矩阵的矩阵，可以通过|A|!=0判断

可以发现后面的矩阵为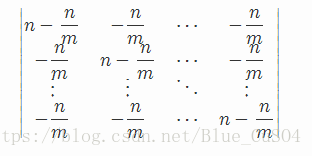这里写图片描述
即主对角线为n-n/m，其余为-n/m的矩阵

这里写图片描述
~~然而打表找规律才是这道题目的正确打开方式~~

这道题目需要用快速乘，而且快速幂的时候也要快速乘，不然GG

题解中部分图片引自dalao，侵删

代码：

#include <cstdio>
#define LL long long 
using namespace std;
LL n,m,p;
LL ksc(LL a,LL k)
{
    LL ans=0;
    for (;k;k>>=1,a=2ll*a%p)
      if (k&1) ans=(ans+a)%p;
    return ans;
}
LL ksm(LL a,LL k)
{
    LL ans=1; a%=p;
    for (;k;k>>=1,a=ksc(a,a))
      if (k&1) ans=ksc(ans,a);
    return ans;
}
int main()
{
    scanf("%lld%lld%lld",&n,&m,&p);
    printf("%lld",ksc(ksm(n,m-1),ksm(m,n-1)));
}